一下子理解海明码

前提：

1.最多只能检测出两位错，或者检测出一位错并能纠正，这里只讨论检一纠一的情况

2.会用到奇偶校验法，默认使用偶校验

发送方：

若数据为“1100”，长度n=4

1.计算校验码所需要的位数k ，使满足 : 2^k >= n+k+1

    此时k=3，满足2^3>=4+3+1 

    于是数据总位数共n+k=7位，从高到低设为H7,H6,.......,H1

2.留出2的幂次方，作为校验码在数据中的位置

   即第2^0位，第2^1位，第2^2位.....

    这里即H1，H2，H4为校验位，位值待求，其余皆为数据位，依次存放待发送数据

      

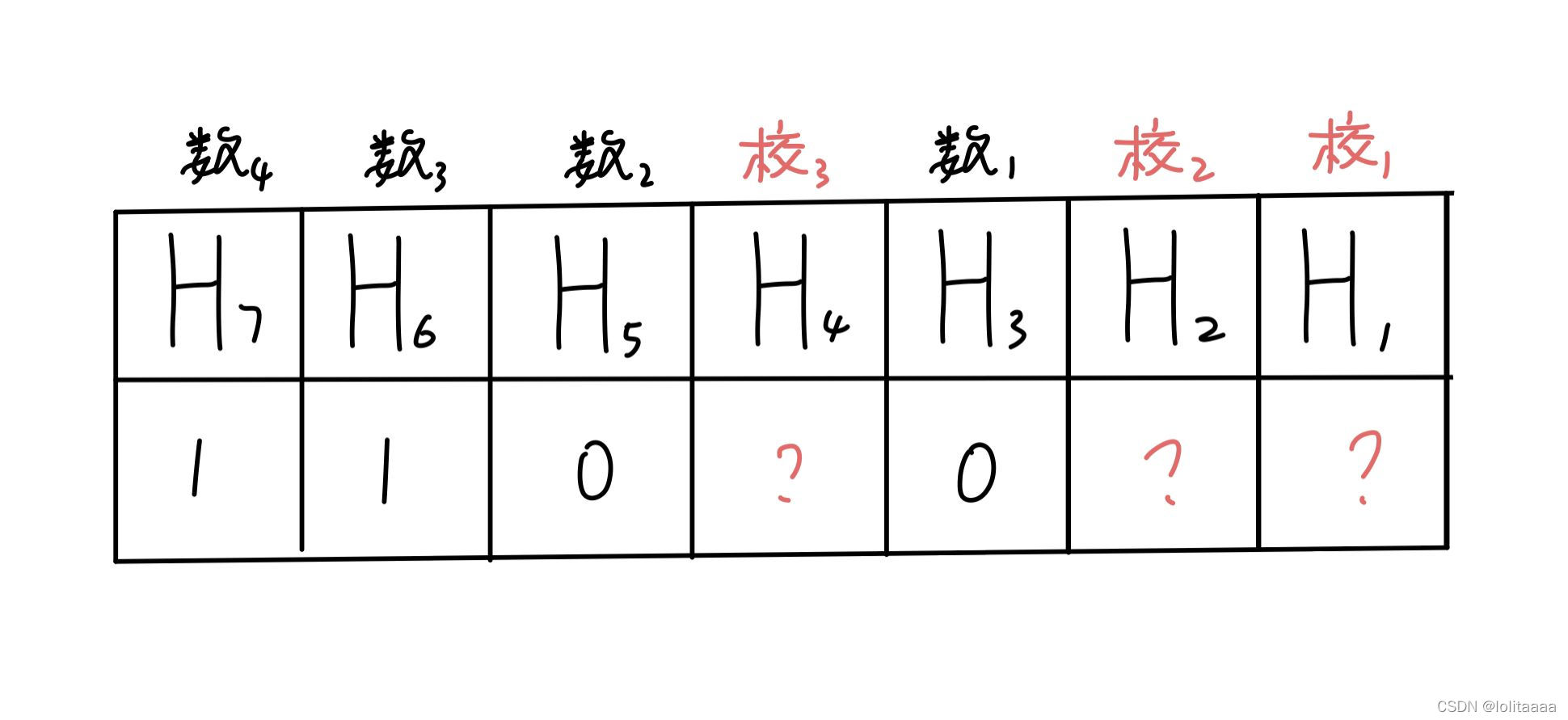
3.分组，确定每个校验位用来校验哪些数据位

    （分组方法：

            先将校验码的位置用二进制表示，将二进制中的1不变，0做通配符，

            然后将数据位的位置也用二进制表示，并与其匹配）

            如图

—————

4.根据偶校验原理，确定每组校验位的位值

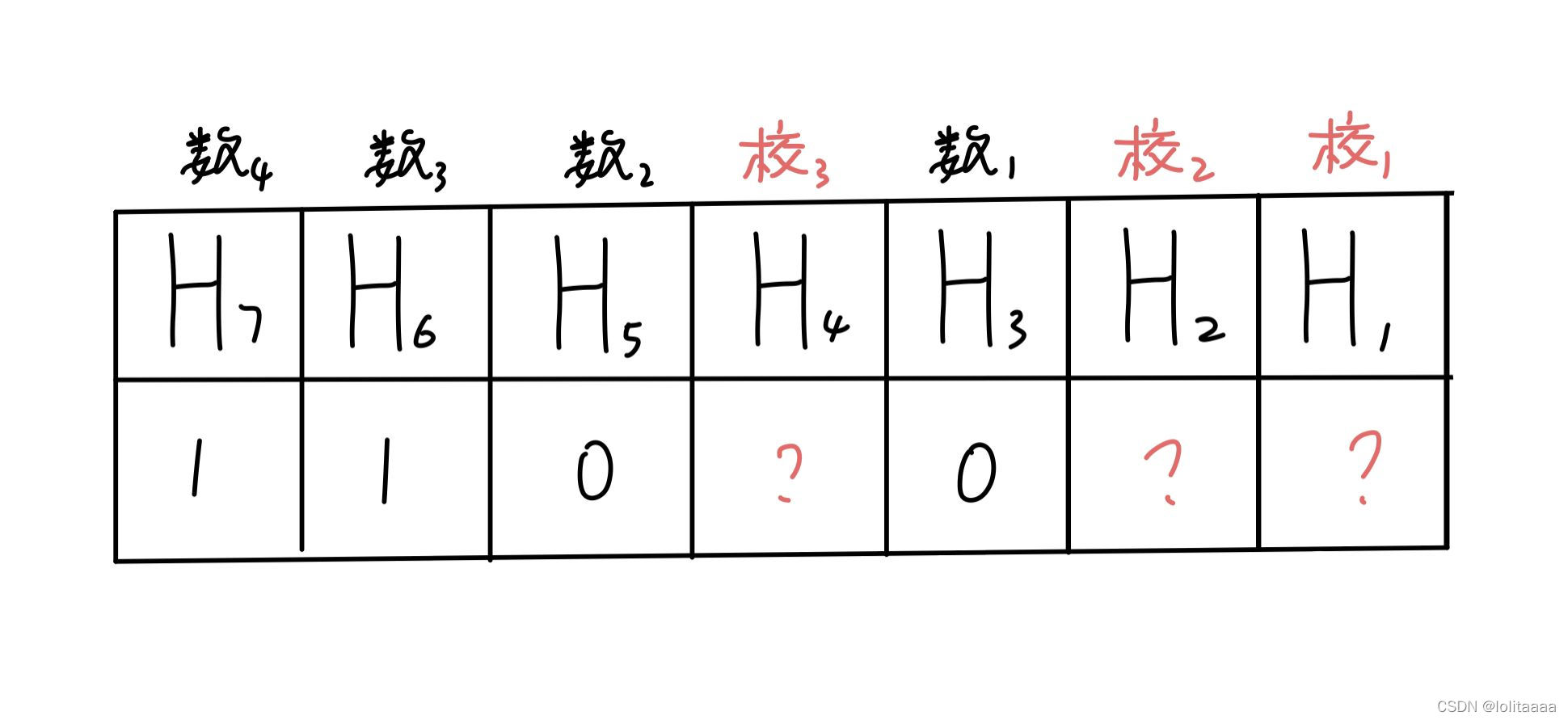
第一组：H1校验H7,H5,H3,即100，有奇数个1，根据偶校验，H1应=1

第二组：H2校验H7,H6,H3,即110，有偶数个1，根据偶校验，H2应=0

第三组：H4校验H7,H6,H5,即110，有偶数个1，根据偶校验，H4应=0

即最终应发送数据为“1100001”

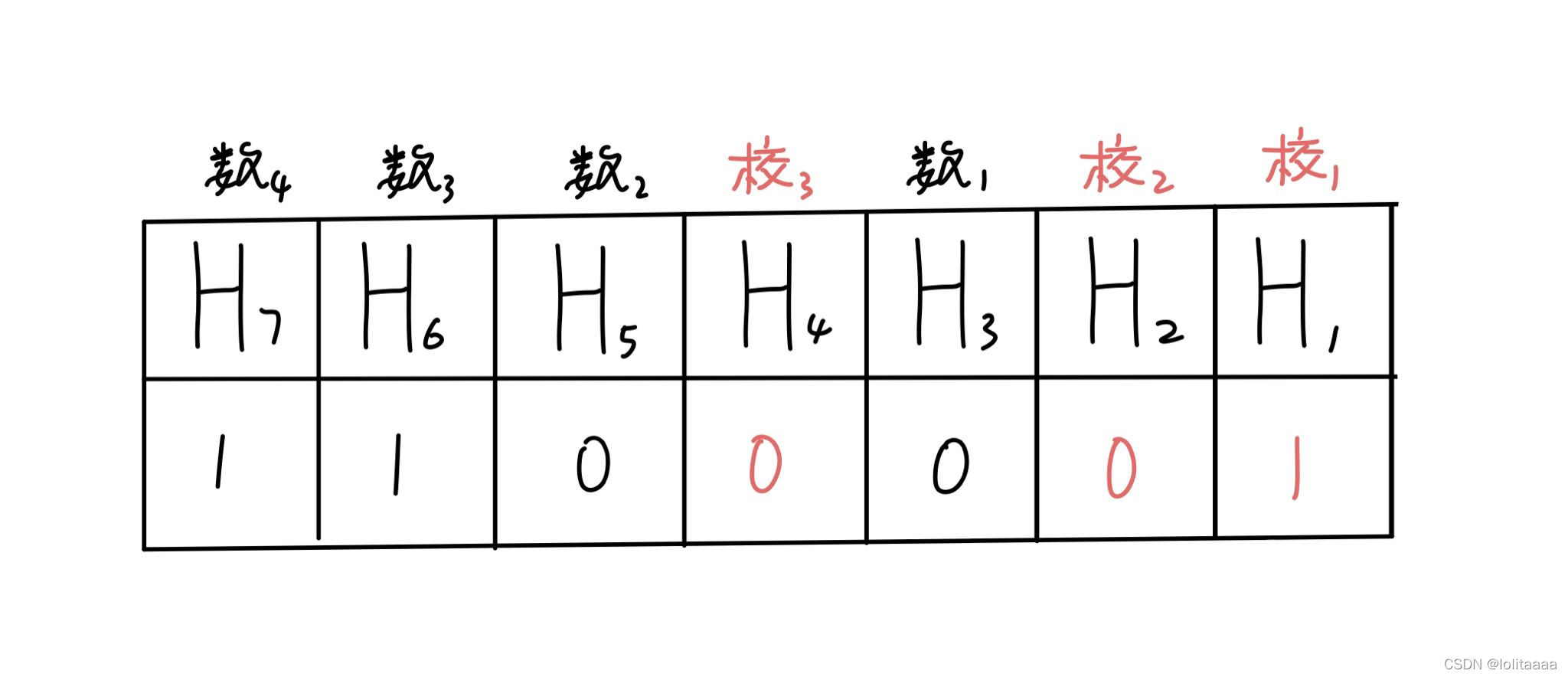
接收方：

1.从低到高，逐组查看校验位。若符合本组偶校验，则记标志S=0；若不符合偶校验，记标记S=1

        若收到“1000001”，H1=“1”检验H7H5H3=“100” ，本组偶校验通过，置S1=0

        H2=“0”校验H7H6H3=“100”，本组偶校验不通过，置S2=1

        同理，H4所属组，偶校验不通过，置S3=1

2.每组标记共同组成的二进制数值，代表着出错位的位置

        这里S3S2S1=“110”，即代表第6位（H6）出错

        若S3S2S1=“000”，则表示数据未出错（因为没有H0）

        #海明码 #计算机网络 #408 #考研