信道带宽
无线信号收端和发端的信道通常由多条路径组成,假设只有两条路径,延时不同。发射信号为f(t)f(t)f(t),两个时延分别为τ0、τ1=τ0+τ\tau_0 、\tau_1 = \tau_0 + \tauτ0、τ1=τ0+τ,接收信号为:
r(t)=Af(t−τ0)+Af(t−τ0−τ)r(t) = Af(t-\tau_0) + Af(t-\tau_0-\tau)r(t)=Af(t−τ0)+Af(t−τ0−τ)
傅里叶变换为:
R(w)=AF(w)ejwτ0+AF(w)e−jw(τ0+τ)=AF(w)ejwτ0(1+e−jwτ)R(w) =AF(w)e^{jw\tau_0} + AF(w)e^{-jw(\tau_0+\tau) } = AF(w)e^{jw\tau_0}(1 + e^{-jw\tau})R(w)=AF(w)ejwτ0+AF(w)e−jw(τ0+τ)=AF(w)ejwτ0(1+e−jwτ)
x信道的频谱函数为
H(w)=R(w)F(w)=Ae−jwτ0(1+e−jwτ)H(w) = \frac{R(w)}{F(w)} = Ae^{-jw\tau_0}(1+e^{-jw\tau})H(w)=F(w)R(w)=Ae−jwτ0(1+e−jwτ)
∣H(w)∣|H(w)|∣H(w)∣随www变化,即无线信道具有频率选择性衰落。
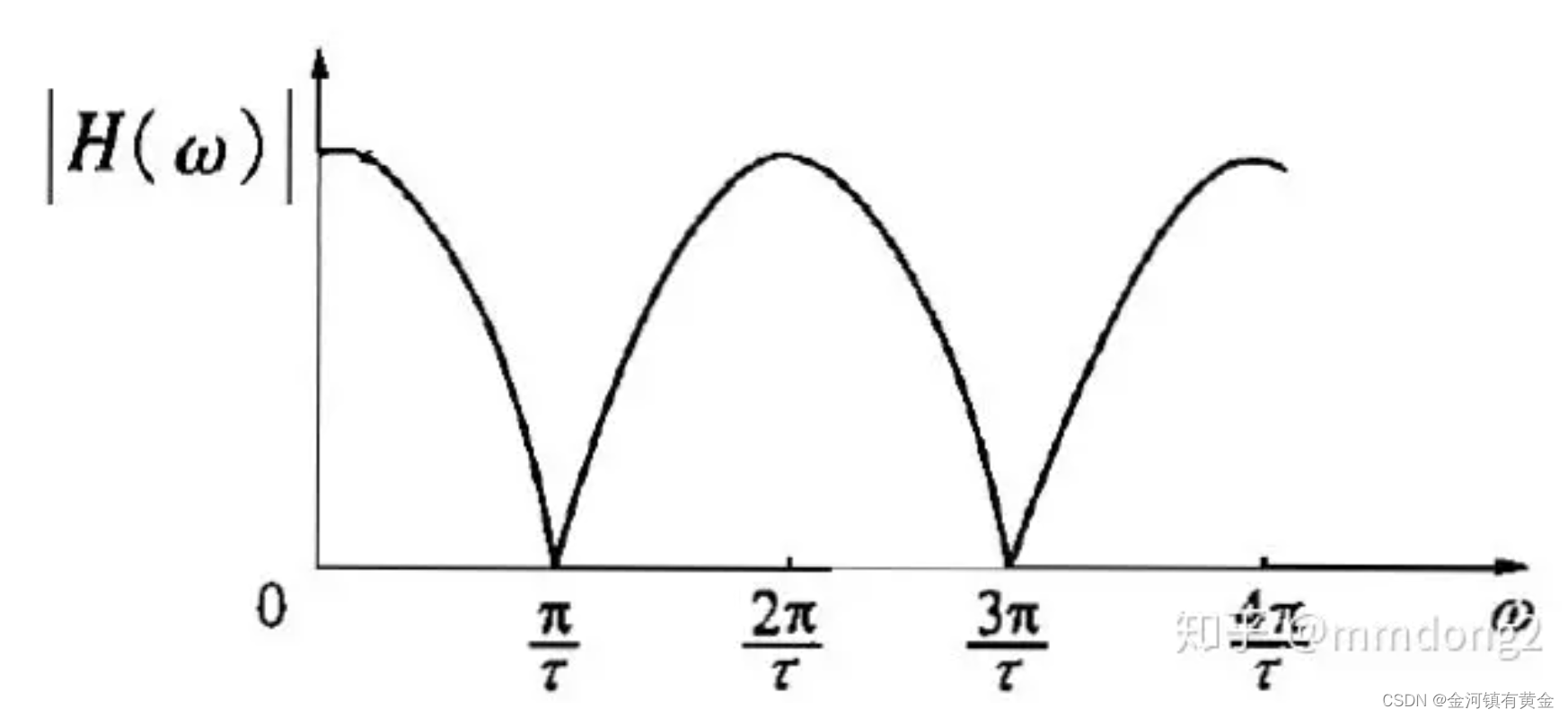
定义第一个波瓣为信道带宽,带宽为
B=w2π=π/τ2π=12τB = \frac{w}{2\pi} = \frac{\pi/ \tau}{2\pi} = \frac{1}{2\tau}B=2πw=2ππ/τ=2τ1
信道带宽与两条路径的相对时延有关,该相对时延称为多径的时延扩展。
信道带宽:
B=12(最大路径时延−最小路径时延)B = \frac{1}{2(最大路径时延-最小路径时延)}B=2(最大路径时延−最小路径时延)1
当信号带宽大于信道带宽,一些频率的信号可以通过,一些频率信号被严重衰减,使整体信号发生畸变。
宽带通信系统需要克服“信号带宽大于信道带宽”。
OFDM
正交频分复用。是一种多载波调制技术。主要指将指定信道分成若干个子信道,在每个子信道上使用一个子载波进行调制,并且各子载波并行传输,有效提高信道的频谱利用率。
正交:频域的每个采样点上,只有一个载波具有非零值,其他所有载波在该采样点上均为零。
2G时代的多址接入方式为TDMA,3G时代为CDMA,4G和5G为OFDMA。
OFDM的核心思想:
将宽频率载波划分为多个带宽较小的正交子载波,并使用正交子载波发送及接收信号。
子载波的带宽小于信道带宽,可以有效克服频率选择性衰落。
带宽B的载波划分为N个带宽为Δf=B/N\Delta f = B/NΔf=B/N的正交子载波。第一个载波的中心频点是f0f_0f0,第n个载波的频点是fn=f0+(n−1)∗Δff_n = f_0 + (n-1)*\Delta ffn=f0+(n−1)∗Δf。将符号XnX_nXn调制到第n个载波上得到传输符号:Xnej2πfntX_n e^{j2\pi f_n t}Xnej2πfnt
N个子载波上的信号累加,最终发送信号为:
f(t)=∑n=1NXnej2πfnt=ej2πf0t∑n=1NXnej2πnΔftf(t) = \sum_{n=1}^{N} X_n e^{j2\pi f_n t} = e^{j2\pi f_0 t} \sum_{n=1}^{N} X_n e^{j2\pi n \Delta f t} f(t)=n=1∑NXnej2πfnt=ej2πf0tn=1∑NXnej2πnΔft
收端接收信号后,通过以下方式确定载波n上传输的符号XnX_nXn:
Δf∫01/Δff(t)e−j2πfntdt=Xn\Delta f \int_0^{1/\Delta f} f(t) e^{-j2\pi f_n t} dt = X_nΔf∫01/Δff(t)e−j2πfntdt=Xn
理论基础:
Δf∫01/Δfej2πfkte−j2πfntdt=1k=n时\Delta f \int_0^{1/\Delta f} e^{j2\pi f_k t} e^{-j2\pi f_n t} dt = 1 \qquad k=n时Δf∫01/Δfej2πfkte−j2πfntdt=1k=n时























 4565
4565

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








