最长上升子序列--动态规划T8

来源：JK老班

题目:给出一个由n个数组成的序列A[1..n]，求最长单调上升子序列（LIS)的长度。LIS即求最大的一个子序列长度m，使得a1<a2<……<am且A[a1]<A[a2]<……<A[am]。

 

输入

两行：

第1行：整数n (1<=n<=1000)

第2行：n个整数 （int范围内），空格隔开。

 

输出

一行：一个整数，即最长上升子序列长度。

 

样例输入

10
63	11	21	36	28	20	57	37	82	4

 

样例输出

5

---

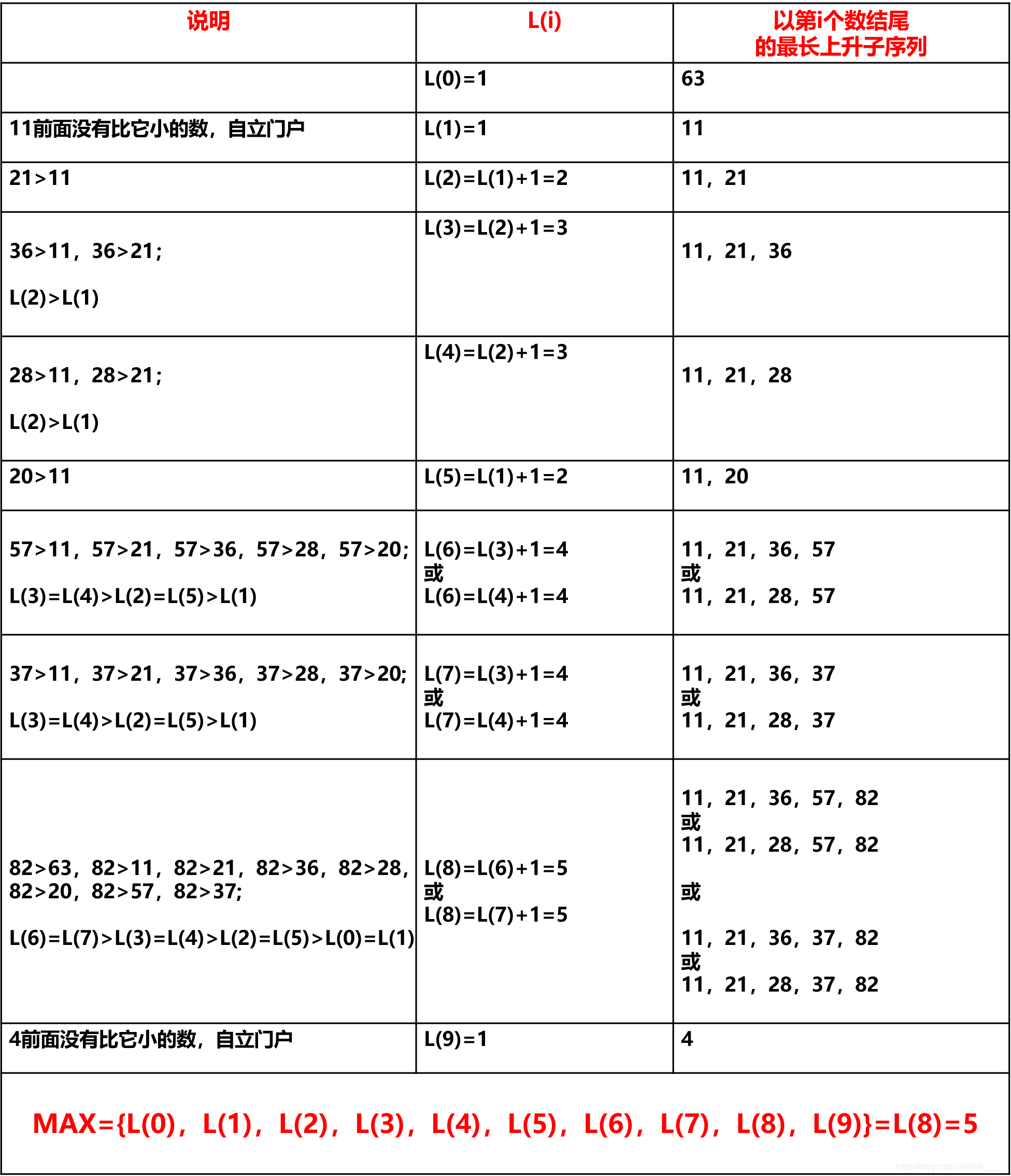
每个数作为结尾的最长上升子序列

遍历，找到前面最长上升子序列的长度，用最长的那个长度加1；

如果找不到，自立门户。

---

 

---

/*
P1556
O(n^2) 
*/

#include<iostream>
using namespace std;
int A[1001]; 
int L[1001]={0}; 

int main(){
    int N; cin>>N;
    for(int i=0;i<N;i++) cin>>A[i];
    
    L[0]=1;
    
    for(int i=1;i<N;i++){
        int max=0;//前面的最长上升子序列长度。 
        for(int j=0;j<i;j++){
            if(A[i]>A[j] && L[j]>max)
            max=L[j];
        }
        L[i]=max+1;//如果max仍是0，长度就为自己等于1 。 
    }
    
    int length=0;
    for(int k=0;k<N;k++){
        if(L[k]>length){
            length=L[k];
        }
    } 
    
    cout<<length;
}