参考链接:
1. 图像分类任务
我们希望根据图片动物的轮廓、颜色等特征,来预测动物的类别,有三种可预测类别:猫、狗、猪。假设我们当前有两个模型(参数不同),这两个模型都是通过sigmoid/softmax的方式得到对于每个预测结果的概率值:
模型1:
| 预测 | 真实 | 是否正确 |
|---|---|---|
| 0.3 0.3 0.4 | 0 0 1 (猪) | 正确 |
| 0.3 0.4 0.3 | 0 1 0 (狗) | 正确 |
| 0.1 0.2 0.7 | 1 0 0 (猫) | 错误 |
模型1对于样本1和样本2以非常微弱的优势判断正确,对于样本3的判断则彻底错误。
模型2:
| 预测 | 真实 | 是否正确 |
|---|---|---|
| 0.1 0.2 0.7 | 0 0 1 (猪) | 正确 |
| 0.1 0.7 0.2 | 0 1 0 (狗) | 正确 |
| 0.3 0.4 0.3 | 1 0 0 (猫) | 错误 |
模型2对于样本1和样本2判断非常准确,对于样本3判断错误,但是相对来说没有错得太离谱。
好了,有了模型之后,我们需要通过定义损失函数来判断模型在样本上的表现了,那么我们可以定义哪些损失函数呢?
1.1 Classification Error(分类错误率)


1.2 Mean Squared Error (均方误差)

我们发现,MSE能够判断出来模型2优于模型1,那为什么不采样这种损失函数呢?主要原因是在分类问题中,使用sigmoid/softmx得到概率,配合MSE损失函数时,采用梯度下降法进行学习时,会出现模型一开始训练时,学习速率非常慢的情况(MSE损失函数)。
有了上面的直观分析,我们可以清楚的看到,对于分类问题的损失函数来说,分类错误率和均方误差损失都不是很好的损失函数,下面我们来看一下交叉熵损失函数的表现情况。
1.3 Cross Entropy Loss Function(交叉熵损失函数)
1.3.1 表达式

上述计算可以使用python的sklearn库
from sklearn.metrics import log_loss
y_true = [[0, 0, 1], [0, 1, 0], [1, 0, 0]]
y_pred_1 = [[0.3, 0.3, 0.4], [0.3, 0.4, 0.3], [0.1, 0.2, 0.7]]
y_pred_2 = [[0.1, 0.2, 0.7], [0.1, 0.7, 0.2], [0.3, 0.4, 0.3]]
print(log_loss(y_true, y_pred_1))
print(log_loss(y_true, y_pred_2))
____________
1.3783888522474517
0.6391075640678003 可以发现,交叉熵损失函数可以捕捉到模型1和模型2预测效果的差异。
2. 函数性质
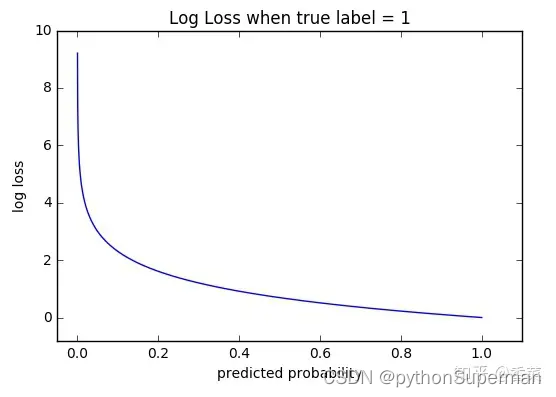
可以看出,该函数是凸函数,求导时能够得到全局最优值。
3. 学习过程
交叉熵损失函数经常用于分类问题中,特别是在神经网络做分类问题时,也经常使用交叉熵作为损失函数,此外,由于交叉熵涉及到计算每个类别的概率,所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。
我们用神经网络最后一层输出的情况,来看一眼整个模型预测、获得损失和学习的流程:
- 神经网络最后一层得到每个类别的得分scores(也叫logits);
- 该得分经过sigmoid(或softmax)函数获得概率输出;
- 模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。
学习任务分为二分类和多分类情况,我们分别讨论这两种情况的学习过程。
nn.CrossEntropyLoss
该标准计算输入 logits 和目标之间的交叉熵损失。
代码实战
该损失函数结合了nn.LogSoftmax()和nn.NLLLoss()两个函数。它在做分类(具体几类)训练的时候是非常有用的。在训练过程中,对于每个类分配权值,可选的参数权值应该是一个1D张量。当你有一个不平衡的训练集时,这是是非常有用的。那么针对这个函数,下面将做详细的介绍。
import torch
import torch.nn as nn
x_input=torch.randn(3,3)#随机生成输入
print('x_input:\n',x_input)
y_target=torch.tensor([1,2,0])#设置输出具体值 print('y_target\n',y_target)
#计算输入softmax,此时可以看到每一行加到一起结果都是1
softmax_func=nn.Softmax(dim=1)
soft_output=softmax_func(x_input)
print('soft_output:\n',soft_output)
#在softmax的基础上取log
log_output=torch.log(soft_output)
print('log_output:\n',log_output)
#对比softmax与log的结合与nn.LogSoftmaxloss(负对数似然损失)的输出结果,发现两者是一致的。
logsoftmax_func=nn.LogSoftmax(dim=1)
logsoftmax_output=logsoftmax_func(x_input)
print('logsoftmax_output:\n',logsoftmax_output)
#pytorch中关于NLLLoss的默认参数配置为:reducetion=True、size_average=True
nllloss_func=nn.NLLLoss()
nlloss_output=nllloss_func(logsoftmax_output,y_target)
print('nlloss_output:\n',nlloss_output)
#直接使用pytorch中的loss_func=nn.CrossEntropyLoss()看与经过NLLLoss的计算是不是一样
crossentropyloss=nn.CrossEntropyLoss()
crossentropyloss_output=crossentropyloss(x_input,y_target)
print('crossentropyloss_output:\n',crossentropyloss_output)最后计算得到的结果为:
x_input: tensor([[ 2.8883, 0.1760, 1.0774], [ 1.1216, -0.0562, 0.0660], [-1.3939, -0.0967, 0.5853]]) y_target tensor([1, 2, 0]) soft_output: tensor([[0.8131, 0.0540, 0.1329], [0.6039, 0.1860, 0.2102], [0.0841, 0.3076, 0.6083]]) log_output: tensor([[-0.2069, -2.9192, -2.0178], [-0.5044, -1.6822, -1.5599], [-2.4762, -1.1790, -0.4970]]) logsoftmax_output: tensor([[-0.2069, -2.9192, -2.0178], [-0.5044, -1.6822, -1.5599], [-2.4762, -1.1790, -0.4970]]) nlloss_output: tensor(2.3185) crossentropyloss_output: tensor(2.3185)
通过上面的结果可以看出,直接使用pytorch中的loss_func=nn.CrossEntropyLoss()计算得到的结果与softmax-log-NLLLoss计算得到的结果是一致的。
接受的都是logits和标签值?
是的,nn.CrossEntropyLoss函数通常接受Logits和标签值作为输入。在PyTorch中,nn.CrossEntropyLoss是一种常用的损失函数,用于多分类问题。
具体地,CrossEntropyLoss函数将Logits作为模型的输出,并根据Logits和对应的标签值计算损失。它首先应用Softmax函数将Logits转换为概率分布,然后计算预测概率分布与真实标签之间的交叉熵损失。
在使用CrossEntropyLoss函数时,通常需要将模型的输出(Logits)和对应的真实标签传递给该函数。函数内部会自动进行Logits的Softmax转换和交叉熵损失的计算。最终,该函数返回表示损失的标量值,可以用于模型的优化和训练过程。
因此,当使用nn.CrossEntropyLoss函数时,通常将Logits作为模型的输出,并将对应的真实标签作为目标值传递给该函数。
解释变形代码
def cross_entropy(self, logits, onehot_labels, ls=False):
if ls:
onehot_labels = 0.9 * onehot_labels + 0.1 / logits.size(-1)
return (-1.0 * torch.mean(torch.sum(onehot_labels * F.log_softmax(logits, -1), -1), 0))流程解释
-
输入参数:
logits:模型的原始输出,即未经过 Softmax 处理的预测结果。onehot_labels:真实标签的 one-hot 编码形式。ls:一个布尔值,表示是否应用标签平滑(Label Smoothing)技术。
-
标签平滑处理:
- 如果
ls参数为True,则执行标签平滑。标签平滑是一种正则化技术,用于减少模型对于训练数据的过拟合。在这里,使用了一种简单的标签平滑方法,将原始的 one-hot 标签onehot_labels中的每个非零元素的值从 1 减小到 0.9,并且将其余的零元素替换为 0.1 / 类别数。这样做的目的是使标签更接近均匀分布,减少模型对训练数据的过度自信。 - 如果
ls参数为False,则跳过标签平滑处理,直接使用原始的 one-hot 标签。
- 如果
-
交叉熵计算:
- 使用 PyTorch 中的
F.log_softmax函数对模型的原始输出logits进行 softmax 操作,并取对数,以获得归一化的对数概率值。这样可以避免在计算交叉熵时出现数值不稳定性问题。 - 将经过 softmax 处理后的输出与经过标签平滑处理后的 one-hot 标签相乘,得到一个张量,表示每个类别的交叉熵损失。
- 使用
torch.sum对每个样本的损失进行求和,并使用torch.mean对批量中的样本损失进行求平均,得到最终的损失值。 - 最后,将损失值取负号,得到交叉熵损失的负值,作为函数的返回值。
- 使用 PyTorch 中的
logits.size(-1)是什么意思
logits.size(-1) 表示在 PyTorch 张量 logits 的最后一个维度的大小。这种用法是 PyTorch 中的一种便捷方式,可以用来获取张量的特定维度的大小,而无需显式地指定维度的索引。
具体来说,size() 方法返回一个包含张量各个维度大小的元组,例如 (batch_size, num_classes)。通过在 size() 方法中传入参数 -1,PyTorch 将会自动选择最后一个维度的大小,因此 logits.size(-1) 就等价于 logits.size()[最后一个维度的索引],即模型输出的类别数量。这种方式在处理动态维度的情况下特别有用,因为它能够保证代码的通用性和灵活性,无需显式指定维度的索引值。
流程的例子解释
import torch
import torch.nn.functional as F
# 定义一个示例的 logits 和 onehot_labels
logits = torch.randn(3, 5) # 假设 batch_size=3, num_classes=5
onehot_labels = torch.tensor([[0, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[1, 0, 0, 0, 0]], dtype=torch.float32) # batch_size=3
class CustomLoss:
def cross_entropy(self, logits, onehot_labels, ls=False):
print("logits shape:", logits.size())
print("onehot_labels shape:", onehot_labels.size())
print("logits.size(-1):",logits.size(-1))
if ls:
onehot_labels = 0.9 * onehot_labels + 0.1 / logits.size(-1)
print("Smoothed onehot_labels:")
print(onehot_labels)
return (-1.0 * torch.mean(torch.sum(onehot_labels * F.log_softmax(logits, -1), -1), 0))
# 实例化自定义损失函数对象
loss_fn = CustomLoss()
# 调用 cross_entropy 方法计算损失
loss = loss_fn.cross_entropy(logits, onehot_labels, ls=True)
print("Final loss:", loss)
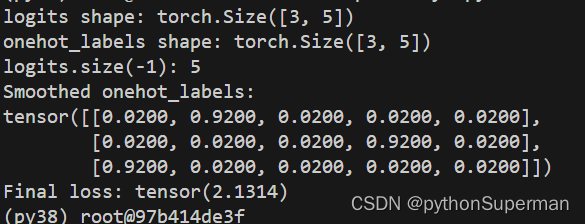
(-1.0 * torch.mean(torch.sum(onehot_labels * F.log_softmax(logits, -1), -1), 0))这段代码是用来计算交叉熵损失的核心部分,让我逐步解释它:
-
F.log_softmax(logits, -1):F.log_softmax函数对模型的原始输出logits进行 softmax 操作,并取对数,以得到归一化的对数概率值。这一步是为了避免在计算交叉熵时出现数值不稳定性问题。
对于每个样本对应的每个类的概率值,softmax得出来的结果和为1,加了log后就不是了
-
onehot_labels * F.log_softmax(logits, -1):- 这一步将经过 softmax 处理后的输出与 one-hot 编码的标签相乘,实现了将真实标签对应的概率值提取出来。
-
torch.sum(onehot_labels * F.log_softmax(logits, -1), -1):torch.sum函数在最后一个维度上求和,这里的最后一个维度对应着类别维度。这样做得到的结果是每个样本的交叉熵损失,因为在最后一个维度上进行了求和操作,所以会得到一个形状为(batch_size,)的张量。
-
torch.mean(torch.sum(onehot_labels * F.log_softmax(logits, -1), -1), 0):torch.mean函数对所有样本的损失值取平均,得到了批量中所有样本的平均交叉熵损失。由于在之前已经对每个样本的损失值进行了求和,所以这里只需在第一个维度上进行求平均,得到一个标量值。
-
(-1.0 * torch.mean(torch.sum(onehot_labels * F.log_softmax(logits, -1), -1), 0)):- 最后,将平均交叉熵损失取负号。这是因为通常情况下,PyTorch 的优化器是通过最小化损失函数来更新模型参数的,而交叉熵损失函数是需要最大化的,因此在实现时一般都会取其负值作为损失值。
让标签形成one-hot编码
targets = torch.tensor([1, 3, 0])
onehot_labels = F.one_hot(targets, outputs.size(-1))
print(outputs.size(-1))
print(onehot_labels)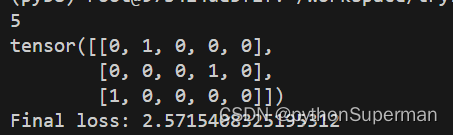
 深度解析:交叉熵损失函数在图像分类中的应用与优势,
深度解析:交叉熵损失函数在图像分类中的应用与优势,





 文章详细介绍了在图像分类任务中,模型1和模型2的预测性能以及MSE和分类错误率作为损失函数的问题。通过比较,文章重点阐述了交叉熵损失函数在捕捉模型精度上的优越性,尤其是在神经网络中的应用,以及结合Softmax函数的特性。
文章详细介绍了在图像分类任务中,模型1和模型2的预测性能以及MSE和分类错误率作为损失函数的问题。通过比较,文章重点阐述了交叉熵损失函数在捕捉模型精度上的优越性,尤其是在神经网络中的应用,以及结合Softmax函数的特性。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








