逆元的乘除法、逆元代码和线性求逆元

今天我给大家继续讲一下逆元以及几道题目。
我们先来看一下逆元的乘除法：

逆元的乘除法

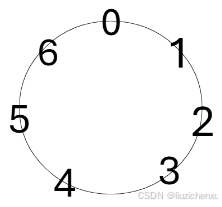
假设 a 和 b 都是小于 p 的非负整数：
a+b 取模 p：(a+b)%p
a-b 取模 p：(a-b+p)%p
+p 相当于在环上多转一圈。如果 a-b 是正数，不影响结果。如果 a-b 是负数，那么正好转换成正数。如果 a 和 b 不一定比p 小，那么我们可以写成：
$$((a-b)\%p+p)\%p$$
a×b 取模 p：a*b%p
a÷b 取模 p：a/b%p 能这么类比吗？
比如 3÷2=1.5，1.5 不在环里。向上取整？向下取整？
有个结论：如果 a 除以 b 等于 c ，那么 c 乘以 b 应当等于a 。
如果选择向下取整：3÷2=1，但是 1×2=2 ，不等于 3 ，不满足以上结论。所以不能向下取整。
如果选择向上取整：3÷2=2，但是 2×2=4，不等于 3 ，不满足以上结论。所以不能向上取整。
并且小数不在模运算的系统中，模运算不会出现小数。所以我们需要找到一个整数能够代表二分之三在模运算中的结果。
逆元（乘法逆元）：在模运算系统中，inv(a)代表 a 分之一。所以乘法逆元也称为“数论倒数”
接下来，我要讲几道题。

逆元的应用

这就是比较典型的求逆元题目,其实求逆元就是快速幂，所以这里就用到了快速幂，只要会快速幂，基本上就会泄露。下面是代码：

但是如果让求的数很大怎么办，这时候，我们就要用到线性求逆元，时间复杂度基本上为O(n)。下面是线性求逆元的代码：

以上就是关于逆元的知识和重点模型题。
（喜欢的点个赞、收个藏呗，不喜勿喷 ）