三次Hermite插值

点击下方图片查看HappyChart专业绘图软件

设$f(x)$在节点$a\le x_0,x_1,\cdots ,x_n\le b$处的函数值为$f_0,f_1,...,f_n$，设$P(x)为f(x)$在区间$[a,b]$上的具有一阶导数的插值函数
（1）若要求$P(x)$在$[a,b]$上具有一阶导数（一阶光滑度）
$$\begin{gathered} P(x_i)=f(x_i)=f_i \\ {P}^{\prime }(x_i)=f^{\prime }(x_i)=f^{\prime },i=0,1,...,n \end{gathered}$$
$P(x)$可以是最高次数为2n+1次多项式，两个节点就可以用$2\times 1+1=3$次多项式作为插值函数。
（2）同样，若要求$P(x)在[a,b]$上具有m阶导数（m阶光滑度），即$P(x)$在节点$x_0,x_1,...,x_n$处必须满足：
$$\begin{gathered} P(x_i)=f(x_i)=f_i \\ {P}^{\prime }(x_i)=f^{\prime }(x_i)=f_i^{\prime } \\ \cdots \\ {P}^{(m)}(x_i)=f^{(m)}(x_i)=f_i^{(m)},i=0,1,...,n \end{gathered}$$
定义：称满足（1）或（2）式的插值问题为Hermite插值，称满足（1）或（2）式的插值多项式$P(x)$为Hermite插值多项式,记为$H_k(x)$,k为多项式次数。

三次Hermite插值

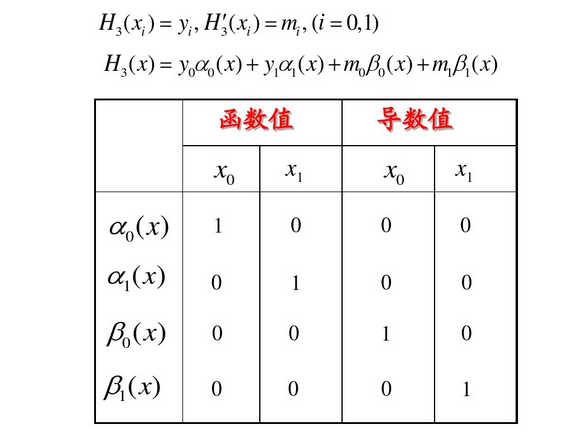
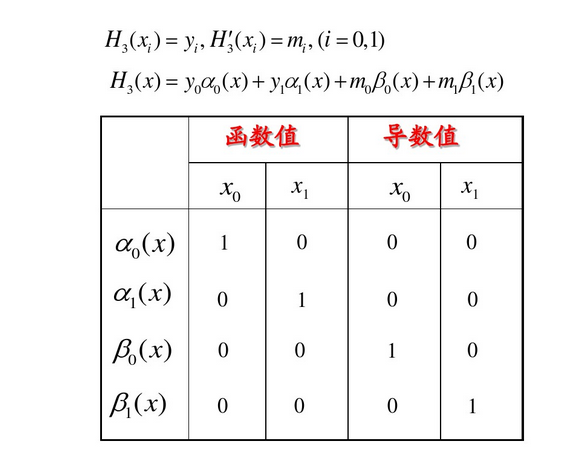
三次Hermite插值余项

$$R_3(x)=\frac{f^{(4)}(\xi )}{4!}(x-x_0{)}^2(x-x_1{)}^2,x_0\le \xi \le x_1$$
当$f^{(4)}(x)在[x_0,x_1]$上存在时，上述公式成立。
#例题