【NOIP2017提高组正式赛】宝藏 题解

【NOIP2017提高组正式赛】宝藏 题解

题目大意

这道题目题目大意就是说，有一个图$G=(V,E)$，求一个子图$G^{\prime }=(V,E^{\prime })$，满足$E^{\prime }=V-1$，也就是一棵树。
然后每一次一条边建出来的花费就是长度乘以这条边起点的深度加一。
求最小花费。

解题方法

关键词：状态压缩动态规划
设$f_{i,j}$表示现在这棵树的深度为$i$，整棵树的状态（用$0/1$表示）为$j$时，的最小花费。
画一个图好看一点。

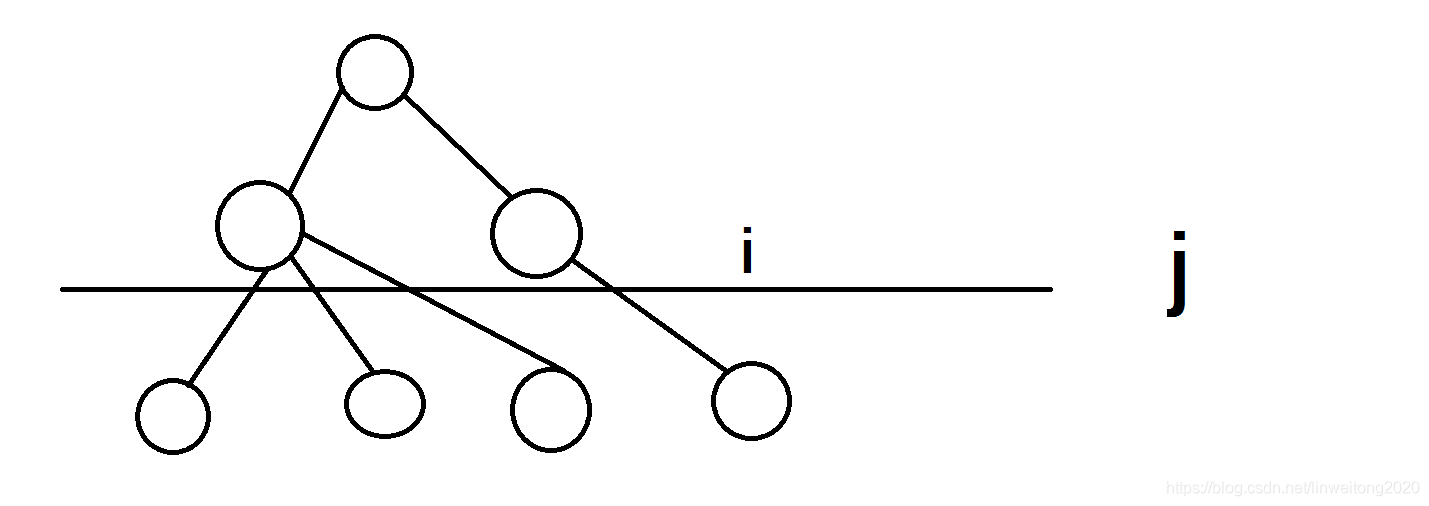
那么显然可以从上一个转移过来。
设$k$表示第$i$层的结点。
则上一层的状态就是$f_{i-1,k\oplus j}$。
画个图就显然了。

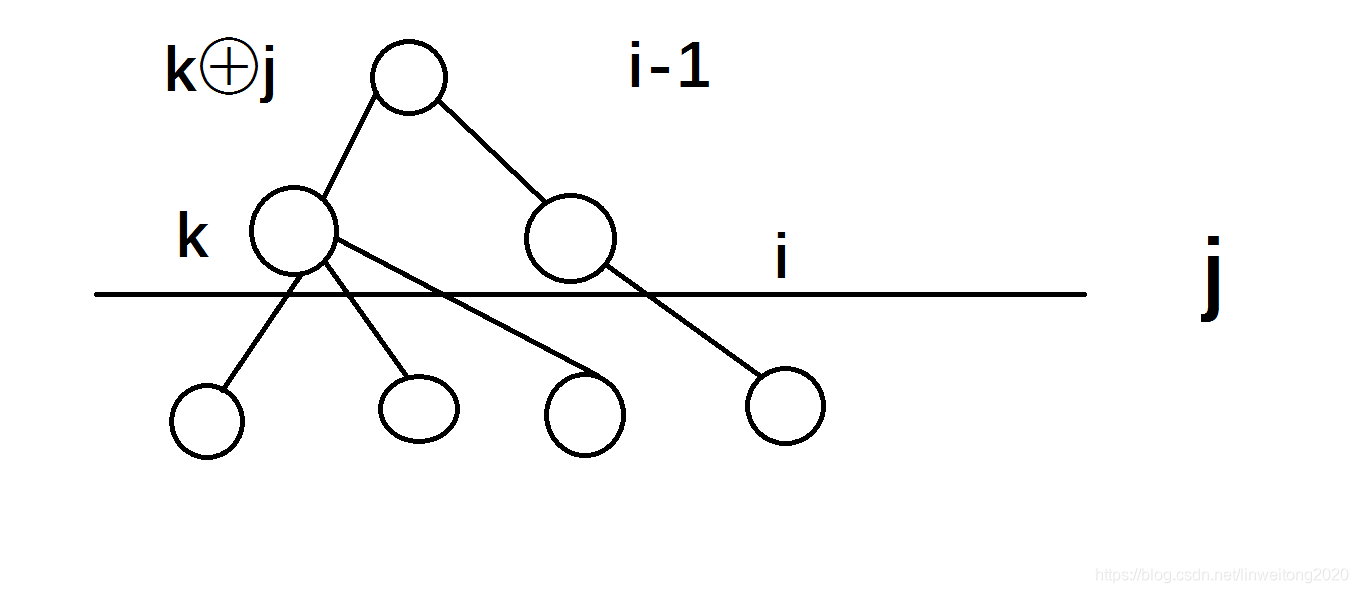
设$g_{p,q}$表示从$1$到某层的上一层的状态为$p$，这一层的状态为$q$。
那么转移就是
$\begin{array}{r}{f}_{i,j}=\underset{k\subseteq j}{\min }{f}_{i-1,j\oplus k}+g_{j\oplus k,k}\times (i-1)\end{array}$
看上图就懂了。
然后考虑如何求$g$。
首先$q$一定是$p$的补集的子集，也就是$q\subseteq {\complement }_{S}p$（设全集（总状态）为$S$），原因很简单。
所以枚举$q$一定是$p\oplus S$的子集（子状态）。

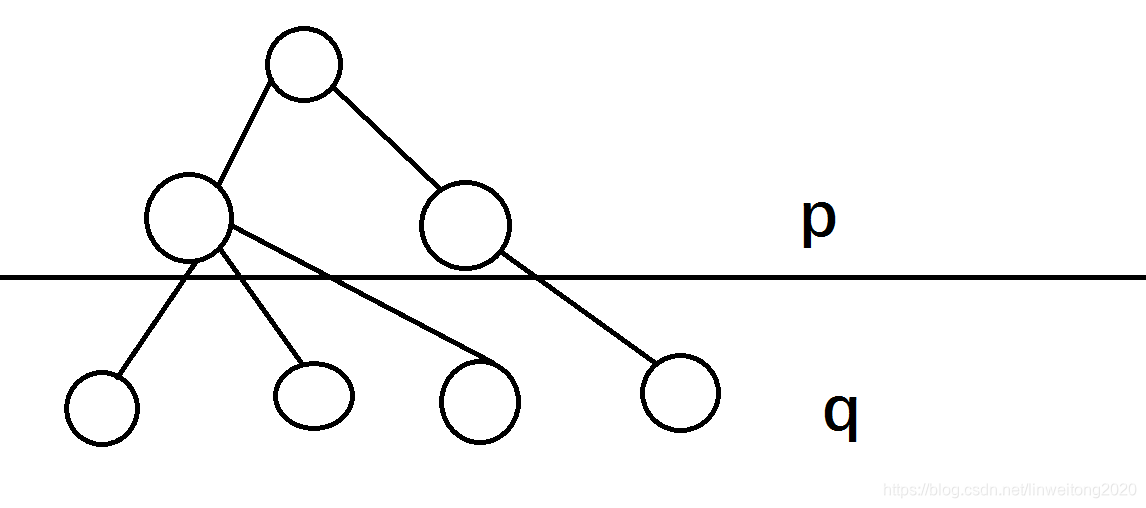
然后我们把状态$q$中所有点都得算一遍，这样就得到了$g_{p,q}$从$g_{p,q\oplus lowbit(q)}$转移过来。
$lowbit(i)$表示二进制$i$从末尾开始第一个$1$所构成的数。
也就是每一次选出一个二进制状态为$lowbit(q)$的点，算这个点的贡献。
这个点设为$x$，其实$x={\log }_2^{lowbit(q)}+1$，原因是我们点是从$1$开始计数的，而二进制状态是从$0$次方开始的。
而贡献就是状态$p$任意一个点到$x$的最小距离。
如图

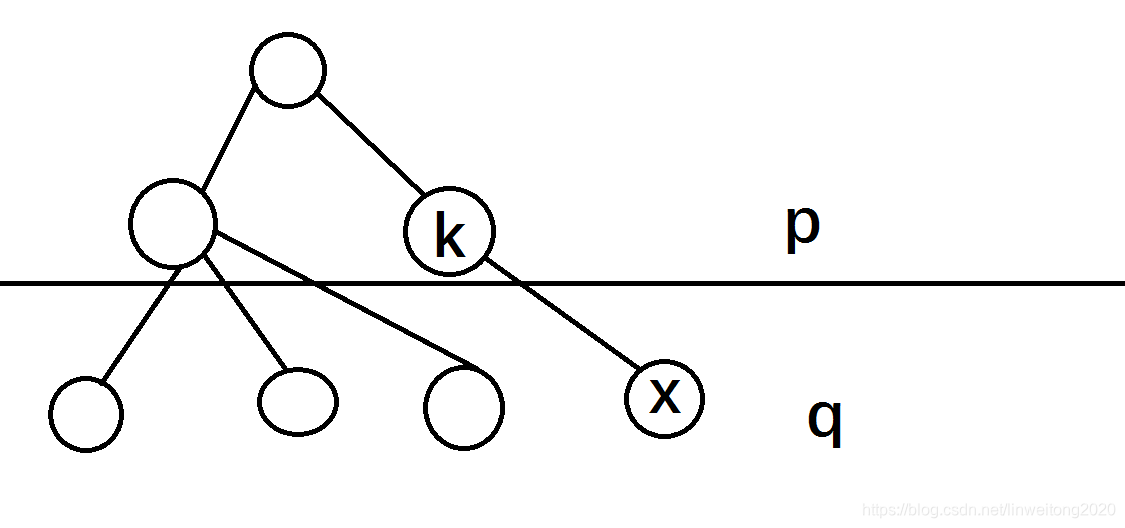
所以可得
$\begin{array}{r}{g}_{p,q}=g_{p,q\oplus lowbit(j)}+\underset{k\in p}{\min }{c}_{k,x}\end{array}$
$c_{i,j}$为$i$到$j$的最小花费。

技巧

假若要枚举$S$的子集，可以用以下代码：

for(int i=S;i;i=(i-1)&S)

但是这样做$i$是不断递减的，所以如果要从小到大枚举要存一个数组再反过来。