【11.8】数学思维-解灯泡开关

一、题目

        初始时有 n 个灯泡处于关闭状态。第一轮，你将会打开所有灯泡。接下来的第二轮，你将会每两个灯泡关闭第二个。

        第三轮，你每三个灯泡就切换第三个灯泡的开关（即，打开变关闭，关闭变打开）。第 i 轮，你每 i 个灯泡就切换第 i 个灯泡的开关。直到第 n 轮，你只需要切换最后一个灯泡的开关。

        找出并返回 n 轮后有多少个亮着的灯泡。

示例 1：

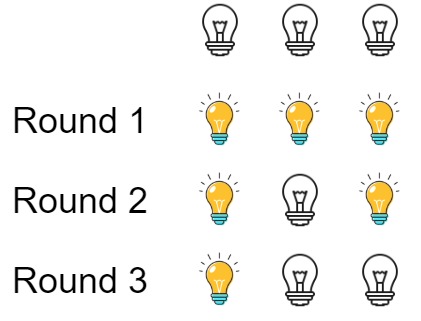
输入：n = 3
输出：1 
解释：
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭]. 

你应该返回 1，因为只有一个灯泡还亮着。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：1

提示：

• 0 <= n <= 10^9

二、解题思路

问题分析

        灯泡初始为关闭状态，经过n轮操作后，最终亮着的灯泡需满足被切换奇数次。关键在于分析每个灯泡被切换的次数。

---

核心思路

1. 操作规则与约数的关联
   第i轮切换所有编号为i的倍数的灯泡。因此，编号为k的灯泡被切换的次数等于k的约数个数。

2. 约数奇偶性的判定

   • 对于非平方数k，其约数总是成对出现（如k=6的约数对为(1,6)和(2,3)），故约数个数为偶数。
   • 对于完全平方数k（如k=9的约数为1,3,9），存在一个中间约数√k不成对，导致约数个数为奇数。

3. 最终结论
   只有完全平方数编号的灯泡最终会亮起，问题转化为计算[1, n]范围内的完全平方数个数，即⌊√n⌋。其中⌊ ⌋表示向下取整。

---

数学推导

• 完全平方数判定：若k可表示为k = m²（其中m为整数），则k的约数个数为奇数。
• 计数公式：在[1, n]中，满足m² ≤ n的最大整数m即为答案，即m = ⌊√n⌋。

三、代码实现

#include <iostream>
#include <cmath>

using namespace std;

int bulbSwitch(int n) {
    return static_cast<int>(sqrt(n + 0.5));// 避免浮点精度误差
}

int main() {
    // 示例测试
    cout << "示例 1：" << endl;
    cout << "输入：n = 3" << endl;
    cout << "输出：" << bulbSwitch(3) << "\n\n";

    cout << "示例 2：" << endl;
    cout << "输入：n = 0" << endl;
    cout << "输出：" << bulbSwitch(0) << "\n\n";

    cout << "示例 3：" << endl;
    cout << "输入：n = 1" << endl;
    cout << "输出：" << bulbSwitch(1) << endl;

    return 0;
}

时间复杂度：O(1)
空间复杂度：O(1)