LeetCode（319 灯泡开关）

最新推荐文章于 2021-12-12 23:53:51 发布

原创最新推荐文章于 2021-12-12 23:53:51 发布 · 215 阅读

0 ·

CC 4.0 BY-SA版权

leetcode刷题java 专栏收录该内容

72 篇文章

订阅专栏

本文探讨了一个经典的灯泡开关谜题，通过分析发现，最终亮着的灯泡数量等同于完全平方数的数量。文章提供了一种高效的算法实现，即计算不大于n的完全平方数的个数，这可以通过取n的平方根并向下取整得到。这种算法避免了指数级的复杂度，实现了简洁快速的解决方案。

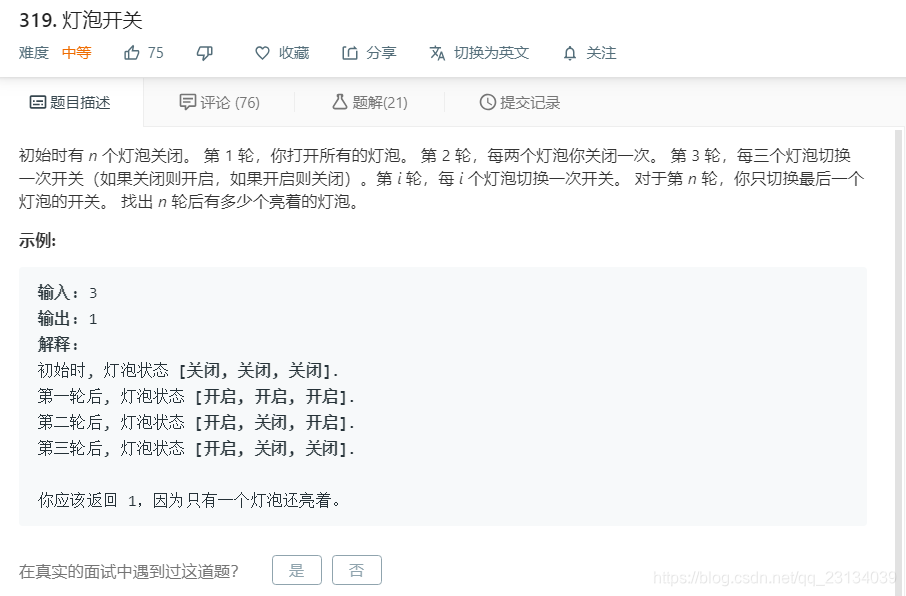
如题在这里插入图片描述
最直观的做法就是模拟每次开关操作，用一个int数组保存状态，每次去判断对应的位置更改对应index的值，但是很显然这是指数即的计算。
那么换个方向，我们就以每个位置会进行开合的次数来判断，很显然开合奇数次则为开启，否则为关闭。那么开合次数是由上面决定的，间隔n不就是对应整除n么，那么对应的就是再该数的所有约数时进行开合操作，而约数都是成对存在的，其中的特殊情况即平方数，拥有一对相同的约数组。由此变成找到不大于n的所有完全平方数

public int bulbSwitch(int n) {
        int count = 0;
        for(int i=1;i<n;i++) {
        	if(i*i<=n) {
        		count++;
        	}else {
        		break;
        	}
        }
        return count;
    }

结果在这里插入图片描述
有点出乎意料。那么有更简洁的写法。完全平方数的个数不就等于该数的平方根的整数部分

public int bulbSwitch1(int n) {
        return (int)Math.sqrt(n);
    }

可以了在这里插入图片描述