2025-1-16算法打卡

一，矩阵置零

1.题目描述：

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

2.实例：

示例 1：

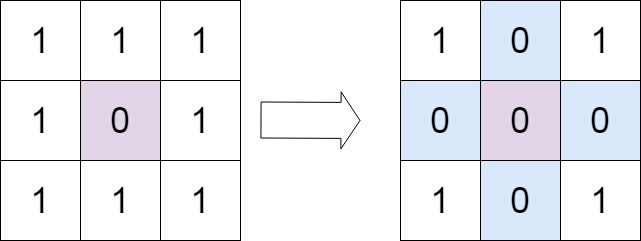
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

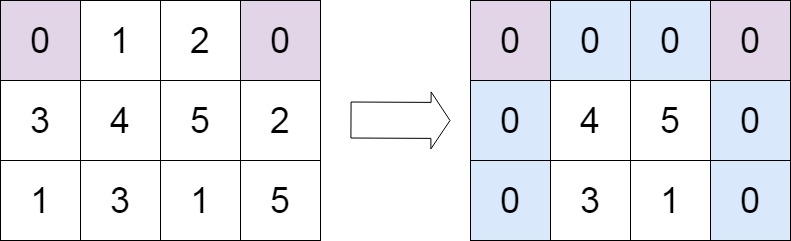
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

3.思路：

思路:用两个变量标记第一行和第一列是否有0，接着循环一遍矩阵，如果遇见0，将和这个网格相同的第一行和第一列的元素标记成0，在循环矩阵，如果当前网格对应的第一行和第一列是0，则将这个单元格置为0。最后如果第一列有0 ，则将这第一列全部置为0,如果第一行有0 ，则将这第一行全部置为0

4：代码：

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean flagCol0 = false, flagRow0 = false;
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                flagCol0 = true;
            }
        }
        for (int j = 0; j < n; j++) {
            if (matrix[0][j] == 0) {
                flagRow0 = true;
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (flagCol0) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
        if (flagRow0) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
    }
}

二，旋转图像

1.题目描述：

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

2.实例：

示例 1：

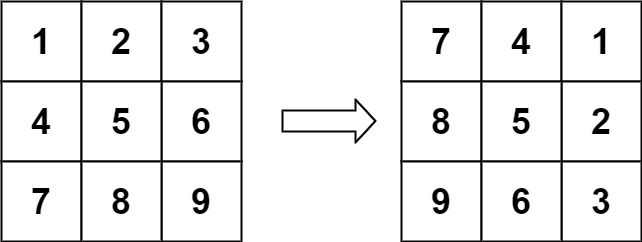
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

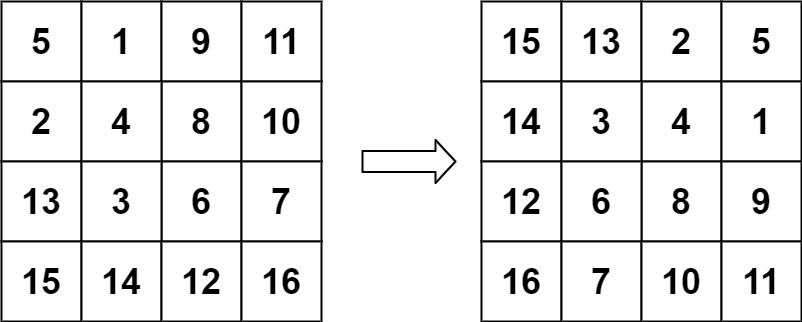
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

3.思路：

自外向内一共有不超过 n/2 层（单个中心元素不算一层）矩形框。对于第 times 层矩形框，其框边长 len=nums−(times∗2)，将其顺时针分为 4 份 len−1 的边，对四条边进行元素的循环交换即可。

4：代码：

class Solution {
    public void rotate(int[][] matrix) {
        if(matrix.length == 0 || matrix.length != matrix[0].length) {
            return;
        }
        int nums = matrix.length;
        int times = 0;
        while(times <= (nums >> 1)){
            int len = nums - (times << 1);
            for(int i = 0; i < len - 1; ++i){
                int temp = matrix[times][times + i];
                matrix[times][times + i] = matrix[times + len - i - 1][times];
                matrix[times + len - i - 1][times] = matrix[times + len - 1][times + len - i - 1];
                matrix[times + len - 1][times + len - i - 1] = matrix[times + i][times + len - 1];
                matrix[times + i][times + len - 1] = temp;
            }
            ++times;
        }       
    }
}