互信息关于先验概率凸性的证明P22314043朱佳奇

摘要

在信息论中，互信息作为一个关键概念，用于衡量两个随机变量之间的信息共享程度。证明互信息是先验概率的上凸函数，对于深入理解信源与信道特性、优化信息传输以及信道容量的研究等方面具有重要意义。本文将详细阐述互信息的定义、先验概率的概念，并逐步推导证明互信息关于先验概率的上凸性质，通过严谨的数学论证过程揭示其内在规律。

一、引言

信息论由克劳德・香农（Claude Shannon）创立，旨在研究信息的量化、存储、传输等问题。互信息作为信息论中的核心度量，在通信系统、数据压缩、模式识别等众多领域有着广泛应用。先验概率作为信源的固有属性，其对互信息的影响是信息论研究的重要内容。深入探讨互信息关于先验概率的凸性，能够为信源编码、信道编码以及通信系统的优化设计提供坚实的理论基础。

二、相关概念介绍

（一）互信息的定义

互信息 I(X;Y) 定义为联合概率分布 p(x,y) 与各自边缘概率分布 p(x) 和 p(y) 的对数比值的期望，即：

它反映了通过观察随机变量 Y 所获得的关于随机变量 X 的信息量，或者反之。

（二）先验概率

先验概率 p(x) 是在不考虑任何观测信息时，信源发出符号 x 的概率分布。它描述了信源的固有不确定性，是信源的基本属性之一。例如，在一个离散信源中，若有符号集 {x1​,x2​,⋯,xn​}，先验概率 p(xi​) 表示信源发出符号 xi​ 的概率，且满足 。

（三）后验概率

后验概率 p(x∣y) 是在已知观测到随机变量 Y 取某个值 y 的条件下，随机变量 X 取某个值 x 的概率。根据贝叶斯定理，后验概率与先验概率、转移概率 p(y∣x) 之间的关系为：

（四）熵与条件熵

信源熵 H(X) 用于衡量信源的不确定性，定义为：

条件熵 H(X∣Y) 表示在已知随机变量 Y 的条件下，随机变量 X 的不确定性，定义为：

互信息与熵、条件熵之间存在重要关系：I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)。

三、证明互信息是先验概率的上凸函数

（一）设定前提

设信源 X 的符号集为 {x1​,x2​,⋯,xn​}，先验概率分布为 p=(p(x1​),p(x2​),⋯,p(xn​))，且 ∑i=1n​p(xi​)=1，p(xi​)≥0，i=1,2,⋯,n。信道转移概率 p(yj​∣xi​) 固定不变，即信道特性已确定。

（二）利用 Jensen 不等式

Jensen 不等式是证明凸函数性质的重要工具。对于一个严格上凸函数 f(x)，若有随机变量 X，其概率分布为 p(x)，则有 E(f(X))≤f(E(X))。

设 f(t)=logt，因为对数函数 f(t)=logt（底数大于 1）是严格上凸函数。

对于互信息 I(X;Y)，可将其展开：

 

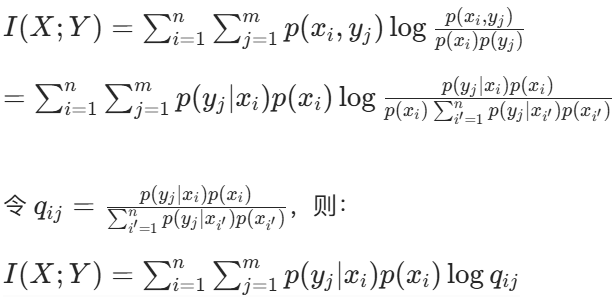
考虑两个不同的先验概率分布 ，以及它们的凸组合 ，0≤λ≤1。

对应的互信息分别为 。

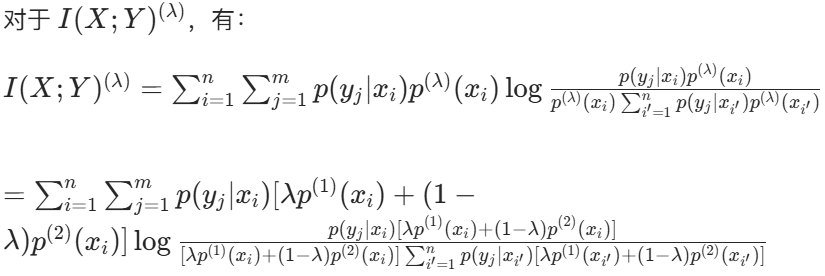
（三）严格上凸性的证明

若要证明严格上凸性，需证明当 且 0<λ<1 时，。

由于对数函数 f(t)=logt 是严格上凸的，根据 Jensen 不等式等号成立的条件，当且仅当对于所有的 i,j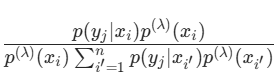，为常数时，等号成立。

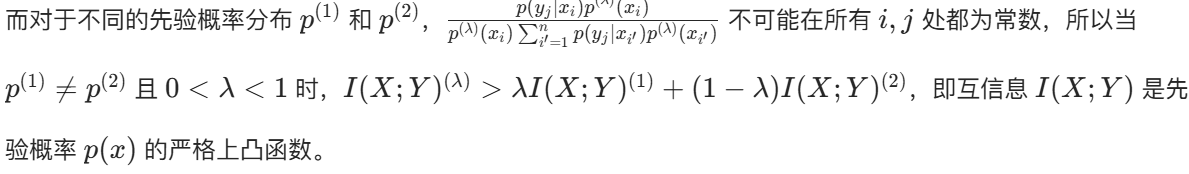
四、结论

通过上述详细的推导证明过程，我们得出在固定信道转移概率的情况下，互信息是先验概率的上凸函数这一重要结论。这一结论在信息论领域有着广泛的应用和深远的意义。在信道容量的研究中，由于互信息是先验概率的上凸函数，对于给定的信道，必然存在一个特定的先验概率分布（匹配信源），使得互信息达到最大值，即信道容量。这为寻找最佳信源分布、优化信道传输效率提供了理论依据。在实际通信系统设计中，可根据信道特性调整信源的先验概率分布，以实现最大的信息传输速率，提高通信系统的性能。同时，该结论也为信息论中其他相关问题的研究奠定了基础，有助于进一步拓展信息论在各个领域的应用。