旋转的左乘与右乘

1. 引言

如果不明确旋转的定义和物理意义，那么本篇文章是没有意义的。本人曾在一本书籍上见到关于绕z轴旋转θ角的两种不同的旋转表示，也了解旋转在不同领域，甚至同一领域的不同应用场景都有不同的物理意义。

旋转的表示有很多种：旋转矩阵，欧拉角，四元数，轴角，李群与李代数。 旋转的应用场景也有很多种：惯性导航，机器人学（机械臂运动学，无人机姿态估计，SLAM等）。

本文将以旋转矩阵为载体，说明旋转（旋转矩阵）左乘与右乘的不同情况。

2. 本文背景

我们首先给出绕x，y，z轴旋转的旋转矩阵表示：1

 

其中，旋转角的正方向由右手螺旋定则给定。注意，绕Y轴旋转的旋转矩阵，-sin在下方。

其实，关于上面三个矩阵，不同书，不同库函数（比如matlab的不同函数，makehgtform与angle2dcm）都不尽相同，我们之所以如此规定，是出于其物理意义。

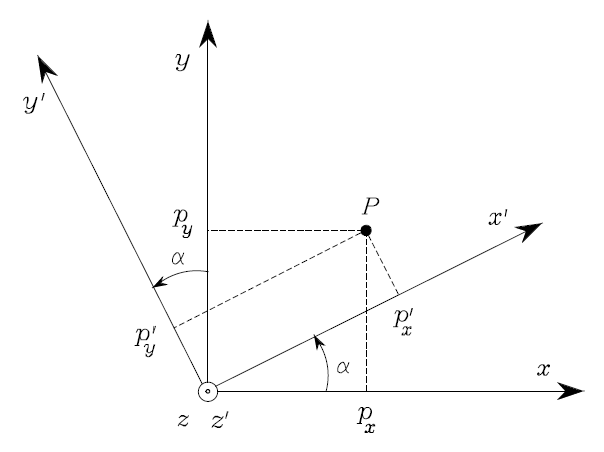
以z轴旋转为例：

2.1 第一种物理意义，坐标系的旋转，其应用场景有SLAM，机械臂运动学等。

 

 

 

 

 

 

 

参考链接

旋转矩阵求解欧拉角Python实现_爬虫虫爬虫虫爬爬爬的博客-优快云博客_python 旋转矩阵转欧拉角

已知向量旋转到新向量 / 向量绕轴旋转--四元数使用的python实现_doubtfire的博客-优快云博客_python 向量 旋转

python 欧拉角，旋转矩阵，四元数之间转换 - 不能说的秘密 - 博客园 (cnblogs.com)

 旋转的左乘与右乘 - 知乎 (zhihu.com)