机器学习-决策树-优快云博客

本文链接：https://blog.youkuaiyun.com/lhxsir/article/details/103653307

本文深入解析决策树算法，包括ID3、C4.5和CART三种主要类型，探讨其工作原理、优缺点及应用场景。并通过实例演示了如何使用Python的sklearn库进行决策树模型的构建与可视化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。比较常用的决策树有ID3，C4.5和CART（Classification And Regression Tree），CART的分类效果一般优于其他决策树。

ID3: 由增熵（Entropy）原理来决定那个做父节点，那个节点需要分裂。对于一组数据，熵越小说明分类结果越好。熵定义如下：
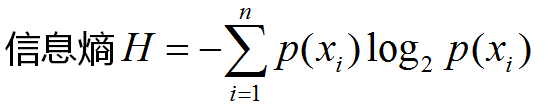
在这里插入图片描述

假如是2分类问题，当A类和B类各占50%的时候，H=1；当只有A类，或只有B类的时候，H=0；所以当H最大为1的时候，是分类效果最差的状态，当它最小为0的时候，是完全分类的状态。因为熵等于零是理想状态，一般实际情况下，熵介于0和1之间。

C4.5算法
实际上，信息增益准则对于可取值数目较多的属性会有所偏好，为了减少这种偏好可能带来的不利影响，C4.5决策树算法不直接使用信息增益，而是使用“信息增益率”来选择最优划分属性。

CART：分类回归树
CART只能将一个父节点分为2个子节点。CART用GINI指数来决定如何分裂。GINI指数：总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似）。

sklearn中使用决策树

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from matplotlib.colors import ListedColormap
iris = datasets.load_iris()
X = iris.data[:,2:] # iris有四个特征，这里取后两个，形成一个坐标点
y = iris.target
# 绘图
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()

# 创建决策树对象，最大深度max_depth为2层，criterion评判标准为entropy（熵）
dt_clt = DecisionTreeClassifier(max_depth=2,criterion='entropy')
# 将训练数据送给模型
dt_clt.fit(X,y)
# 绘制决策边界
def plot_decision_boundary(model, axis): # model是模型，axis是范围
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

# 数据可视化
plot_decision_boundary(dt_clt, axis=[0.5,7.5,0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()