在前面的内容中,我们介绍了多种传统方法和集成学习模型。本篇带来 sklearn.neural_network 模块中的 多层感知机(MLP),并结合遥感影像完成从训练评估到整图预测的完整流程。
往期内容和数据链接如下:
🧠 理论与参数要点
多层感知机(MLP, Multi-Layer Perceptron)由多层线性变换与非线性激活函数组成,通过反向传播与优化器不断更新权重,是最基础的前馈神经网络。
-
结构:输入层 → 隐藏层(如 ReLU、Tanh)→ 输出层(Softmax)。
-
优化器:支持
adam、sgd、lbfgs,其中adam适合大多数情况。 -
正则化:参数
alpha控制 L2 正则强度,用于防止过拟合。 -
早停机制:
early_stopping=True时,模型在验证集上若若干轮无提升会自动停止,避免浪费计算。
常用参数:
-
hidden_layer_sizes=(128,64):两层隐藏层,分别含128和64个神经元。 -
activation="relu":非线性激活函数。 -
max_iter=400:最大迭代次数。 -
alpha=1e-4:正则化强度。
💻 代码示例:MLP 分类与整图预测
仅需修改 DATA_DIR 为包含 KSC.mat 和 KSC_gt.mat 的目录,即可运行。
# -*- coding: utf-8 -*-
"""
Sklearn案例⑫:MLP像素级分类 + 全图预测 + 混淆矩阵
"""
import os, numpy as np, scipy.io as sio, matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap, BoundaryNorm
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import (confusion_matrix, classification_report,
accuracy_score, cohen_kappa_score)
# ===== 参数 =====
DATA_DIR = "your_path" # ← 修改为你的数据路径
PCA_DIM = 30
TRAIN_RATIO = 0.3
SEED = 42
# ===== 1. 数据加载 =====
X = sio.loadmat(os.path.join(DATA_DIR, "KSC.mat"))["KSC"].astype(np.float32)
Y = sio.loadmat(os.path.join(DATA_DIR, "KSC_gt.mat"))["KSC_gt"].astype(int)
h, w, b = X.shape
coords = np.argwhere(Y != 0)
labels = Y[coords[:,0], coords[:,1]] - 1
num_classes = int(labels.max() + 1)
# ===== 2. 划分训练/测试集 =====
train_ids, test_ids = train_test_split(
np.arange(len(coords)), train_size=TRAIN_RATIO,
stratify=labels, random_state=SEED
)
train_pixels = X[coords[train_ids,0], coords[train_ids,1]]
test_pixels = X[coords[test_ids,0], coords[test_ids,1]]
# ===== 3. 无泄露预处理 =====
scaler = StandardScaler().fit(train_pixels)
pca = PCA(n_components=PCA_DIM, random_state=SEED).fit(scaler.transform(train_pixels))
X_train = pca.transform(scaler.transform(train_pixels))
X_test = pca.transform(scaler.transform(test_pixels))
y_train, y_test = labels[train_ids], labels[test_ids]
# ===== 4. 定义并训练MLP =====
mlp = MLPClassifier(
hidden_layer_sizes=(128, 64),
activation="relu",
solver="adam",
alpha=1e-4,
learning_rate_init=1e-3,
max_iter=400,
early_stopping=True,
n_iter_no_change=15,
validation_fraction=0.1,
random_state=SEED
)
mlp.fit(X_train, y_train)
# ===== 5. 测试集评估 =====
y_pred = mlp.predict(X_test)
oa = accuracy_score(y_test, y_pred)
kappa = cohen_kappa_score(y_test, y_pred)
cm = confusion_matrix(y_test, y_pred, labels=np.arange(num_classes))
cm_norm = cm / np.maximum(cm.sum(axis=1, keepdims=True), 1)
print(f"OA={oa*100:.2f}% Kappa={kappa:.4f}")
print(classification_report(y_test, y_pred, digits=4, zero_division=0))
# ===== 6. 混淆矩阵(带数字,颜色柔和)=====
fig, axes = plt.subplots(1, 2, figsize=(11, 4.2), constrained_layout=True)
# 计数矩阵
im0 = axes[0].imshow(cm, interpolation='nearest', cmap=plt.cm.YlGnBu, alpha=0.9)
axes[0].set_title("混淆矩阵(计数)")
axes[0].set_xlabel("预测"); axes[0].set_ylabel("真实")
fig.colorbar(im0, ax=axes[0], fraction=0.046, pad=0.04)
for i in range(num_classes):
for j in range(num_classes):
axes[0].text(j, i, str(cm[i, j]), ha='center', va='center',
color='black' if cm[i,j] < cm.max()/2 else 'white', fontsize=9)
# 归一化矩阵
im1 = axes[1].imshow(cm_norm, vmin=0, vmax=1, cmap=plt.cm.OrRd, alpha=0.9)
axes[1].set_title("混淆矩阵(归一化)")
axes[1].set_xlabel("预测"); axes[1].set_ylabel("真实")
fig.colorbar(im1, ax=axes[1], fraction=0.046, pad=0.04)
for i in range(num_classes):
for j in range(num_classes):
axes[1].text(j, i, f"{cm_norm[i,j]*100:.1f}%", ha='center', va='center',
color='black', fontsize=9)
plt.show()
# ===== 7. 整图预测 =====
X_flat = X.reshape(-1, b)
X_flat_pca = pca.transform(scaler.transform(X_flat))
pred_flat = mlp.predict(X_flat_pca).reshape(h, w) + 1
# 调色板
base_cmap = plt.get_cmap('tab20')
colors = [base_cmap(i % 20) for i in range(num_classes)]
cmap = ListedColormap(colors)
boundaries = np.arange(0.5, num_classes + 1.5, 1)
norm = BoundaryNorm(boundaries, cmap.N)
fig2, ax2 = plt.subplots(figsize=(8.8, 6.6), constrained_layout=True)
im = ax2.imshow(pred_flat, cmap=cmap, norm=norm, interpolation='nearest')
ax2.set_title("MLP 整图预测结果")
ax2.axis('off')
cbar = fig2.colorbar(im, ax=ax2, boundaries=boundaries,
ticks=np.arange(1, num_classes+1, max(1, num_classes//12)),
fraction=0.046, pad=0.04)
cbar.set_label("类别ID", rotation=90)
plt.show()
🔍 结果解读
-
指标:控制台输出 OA、Kappa、精确率、召回率与 F1。
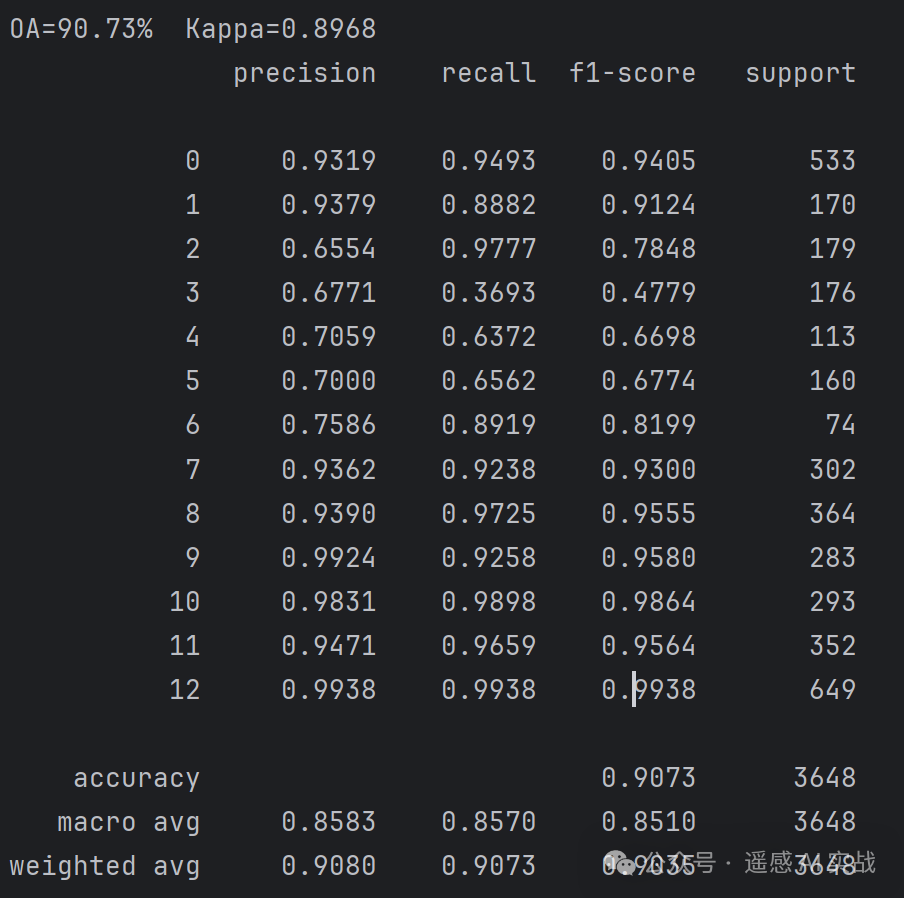
-
混淆矩阵:两个版本(计数与归一化),数字标注清晰显示每类识别情况。
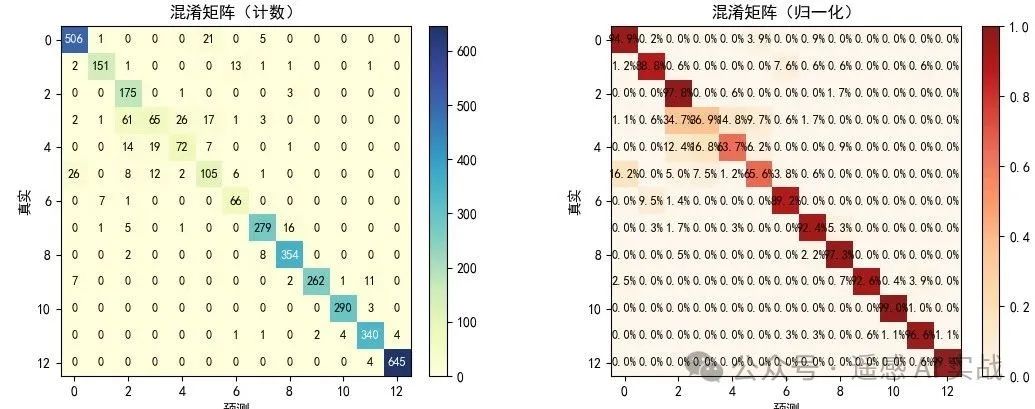
-
整图预测:生成逐像素分类图,可直接观察空间分布效果。
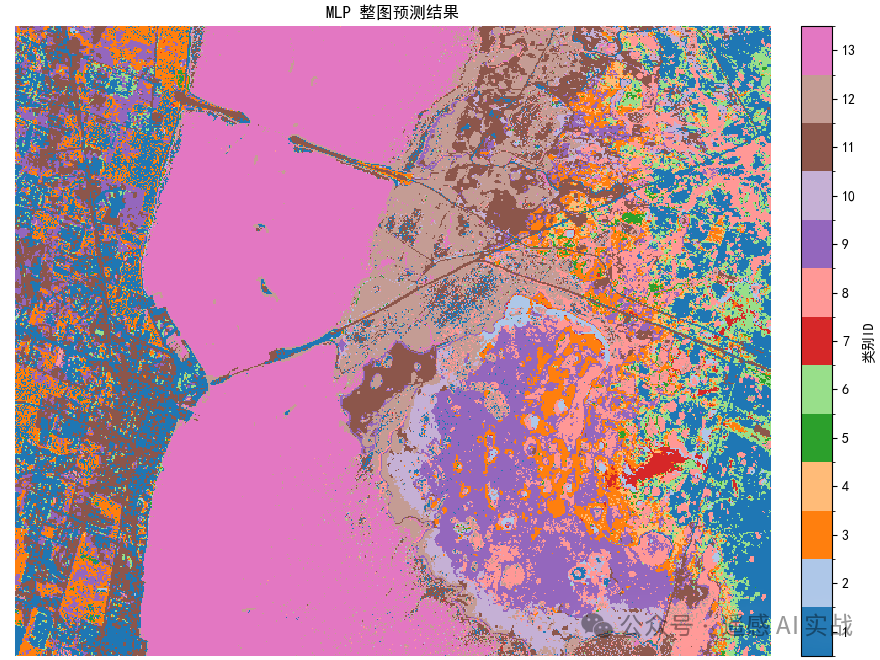
✅ 总结
-
MLP 提供了一个轻量级神经网络基线,结合标准化与 PCA,可用于遥感像素分类。
-
混淆矩阵与整图预测帮助从数值与空间两方面检验模型。
-
调整
hidden_layer_sizes、alpha与activation能显著影响模型表现。
欢迎大家关注下方公众号获取更多内容!






















 6505
6505

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










