FZU ACM 寒假(6)

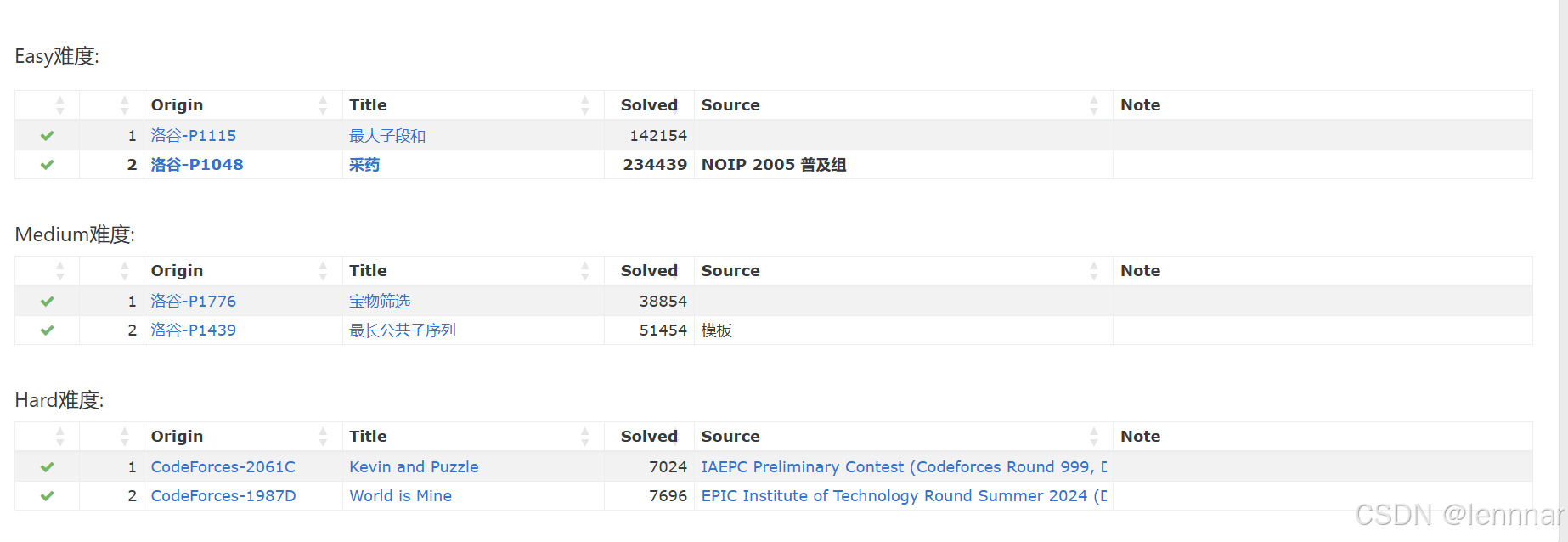
第一题

通过维护一个状态数组dp来记录每个位置的最大子段和,并不断更新全局的最大值maxSum。

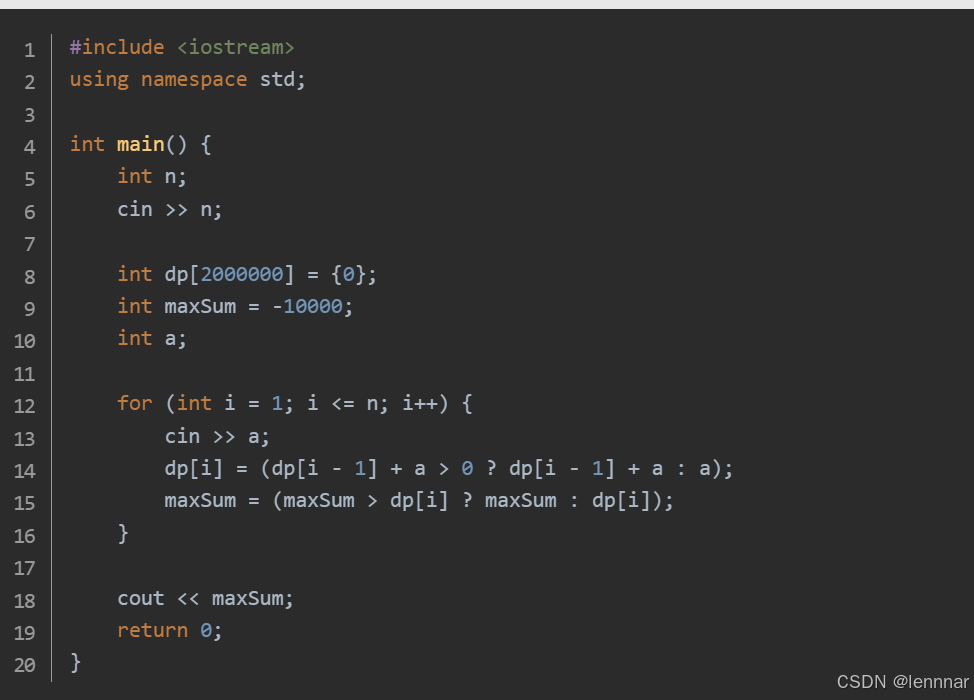
第二题

遍历每株草药，对于每株草药，从总时间t开始向下遍历到该草药的采集时间，更新dp[j]的值。

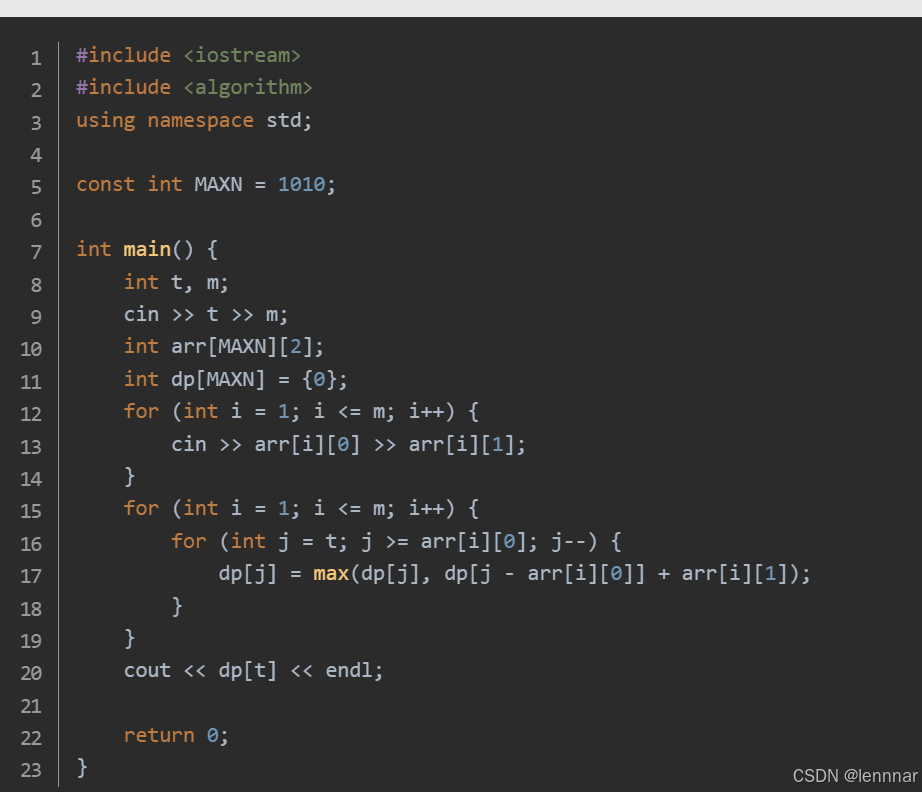
第三题

将每种物品的数量拆分成多个物品：每种物品的数量count被拆分成若干个物品，每个物品的数量都是 k 的倍数，直到 k 大于count。这样，每种物品就被拆分成了多个物品，每个物品的数量都是唯一的。用一个动态规划数组dp来记录最大价值。外层循环遍历所有拆分后的物品，内层循环从 ww递减，更新dp[j]的值。这样可以确保每种物品只被选择一次，避免重复选择

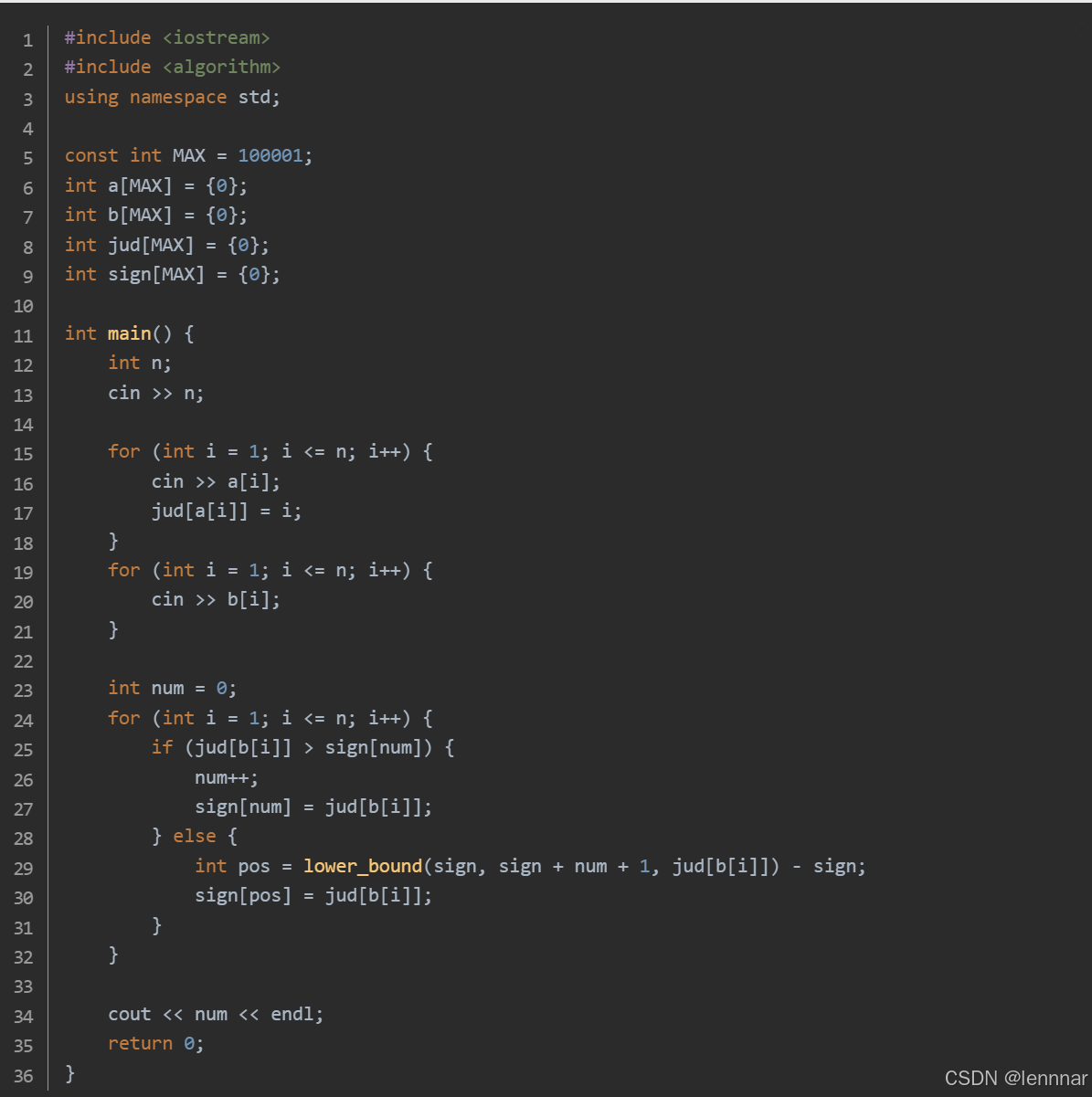
第四题

遍历排列b，对于每个元素b[i]，检查jud[ b[i] ]是否大于sign[num]。如果是，就增加num并更新   sign[num]。否则，找到sign中第一个大于等于jud[b[i]]的位置，并更新该位置的值。

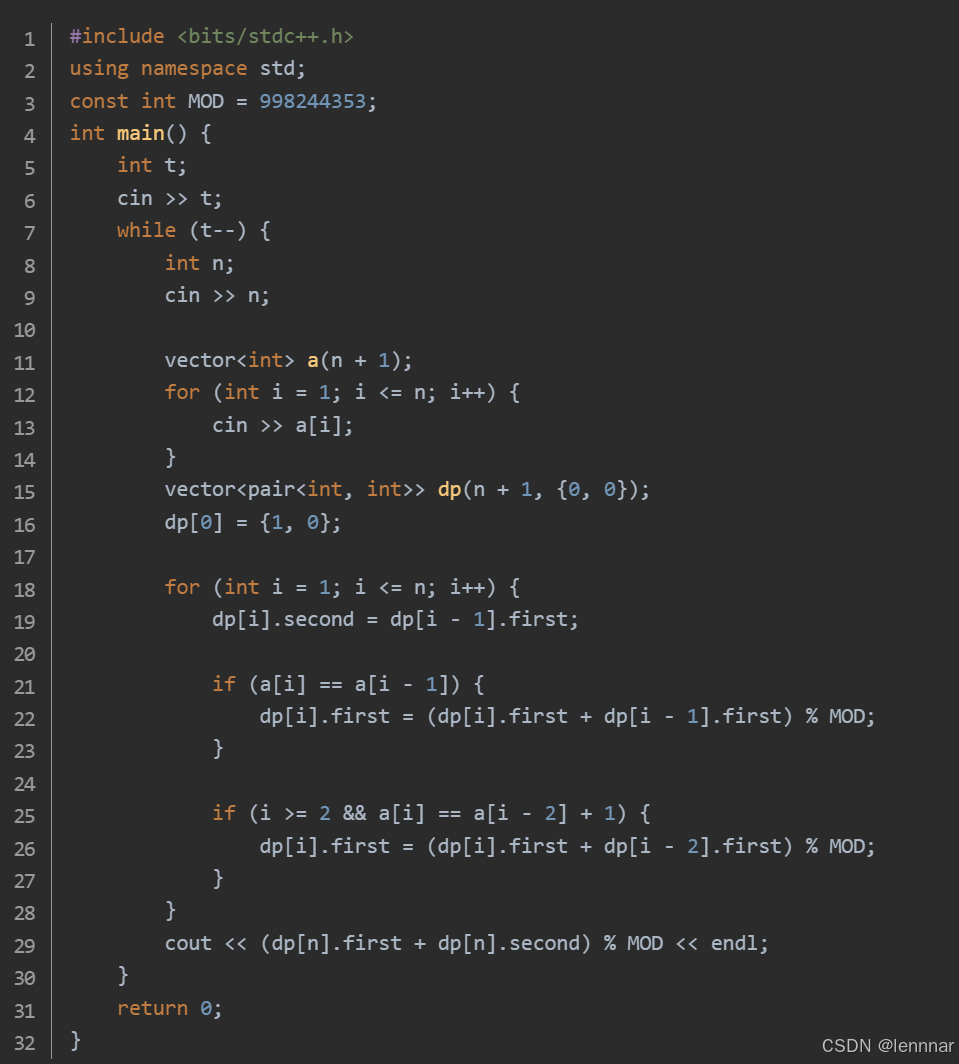
第五题

在循环中，首先将dp[i].second设置为dp[i-1].first，这表示如果第i个人是骗子，那么第i-1个人必须是诚实的，因为骗子不能相邻。接着，代码检查a[i]是否等于a[i-1]。如果是，那么第i个人如果是诚实的，那么a[i]应该等于左边的骗子数，也就是a[i-1]。因此，dp[i].first += dp[i-1].first。然后，代码检查i是否大于等于2，且a[i]是否等于a[i-2] + 1。如果是，那么第i个人如果是诚实的，那么a[i]应该等于左边的骗子数，也就是a[i-2] + 1。因此，dp[i].first += dp[i-2].first。

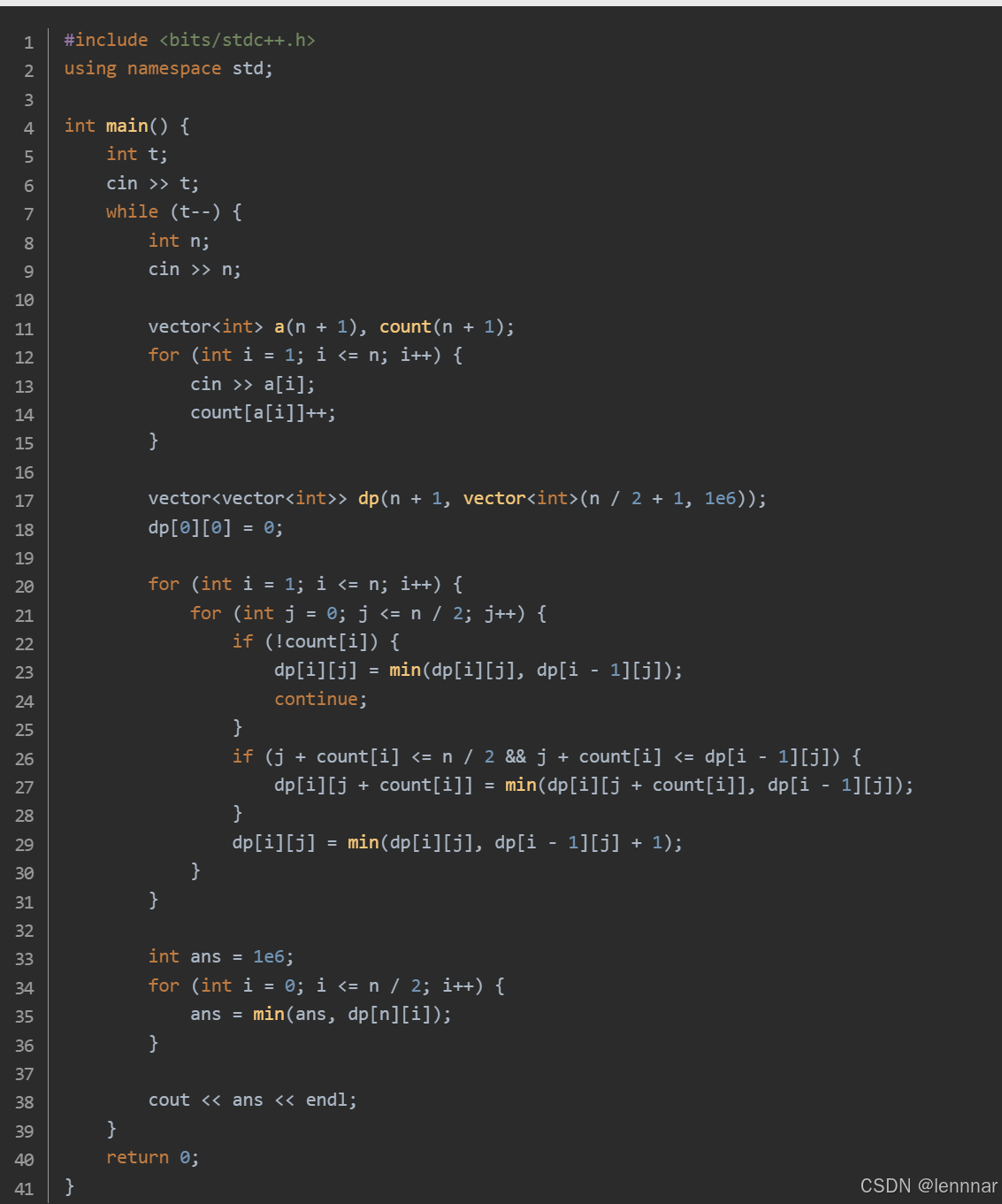
第六题

定义一个二维动态规划数组dp[i][j],表示在前i个美味值中，Alice可以吃到j个蛋糕的最小代价。初始状态dp[0][0]为0，表示没有蛋糕时代价为0。对于每个美味值i，遍历可能的蛋糕数量j，更新dp[i][j]  ：如果当前美味值的蛋糕数量为0，则直接继承前一个状态dp[i-1][j]；如果选择当前美味值的蛋糕，则需要满足j + count[i] <= n/2，并更新dp[i][j + count[i]]为dp[i-1][j]；同时，考虑不选择当前美味值的蛋糕，更新dp[i][j]为dp[i-1][j] + 1  。