CF的连个题目,C1是求边数为4k的正多变形的外接正方形的边长,C2是求边数为4K+2的正多边形的外接正方形的边长。
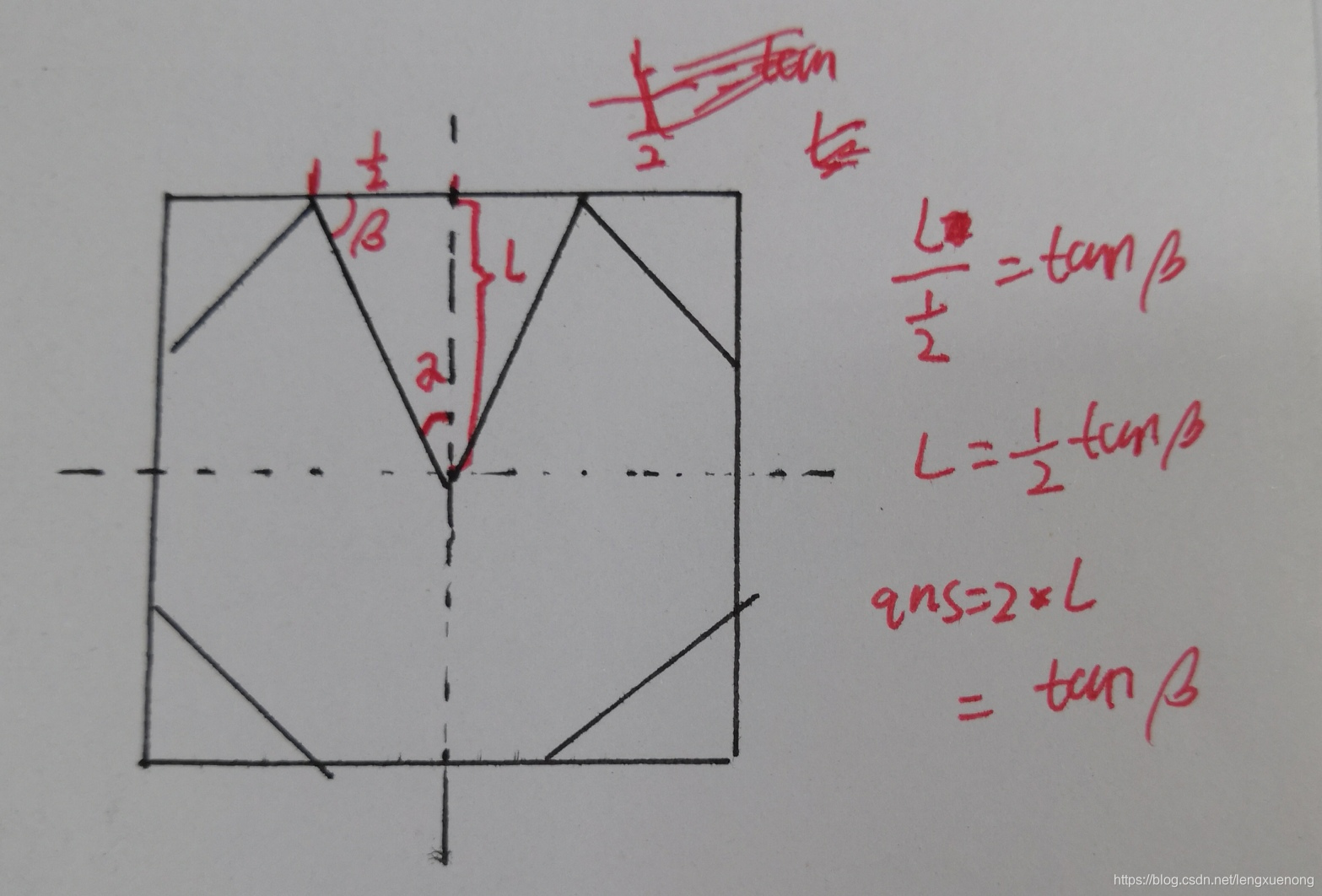
C1可以发现,有4条边与外接正方形重合,那么找出对应的角,再利用三角函数求解。c++提供sin(),cos(),tan()函数,也提供对应的反三角函数acos反余弦函数,asin反正弦函数,atan反正切函数。
#include<bits/stdc++.h>
#define pi 3.1415926535
using namespace std;
int t,n;//一定有四条边与正方形重合。用tan函数算算即可
int main(){
cin>>t;
cout<<setprecision(6)<<fixed;
while(t--){
cin>>n;
n*=2;
cout<<tan(pi*(n-2)/2/n)<<endl;
}
return 0;
}
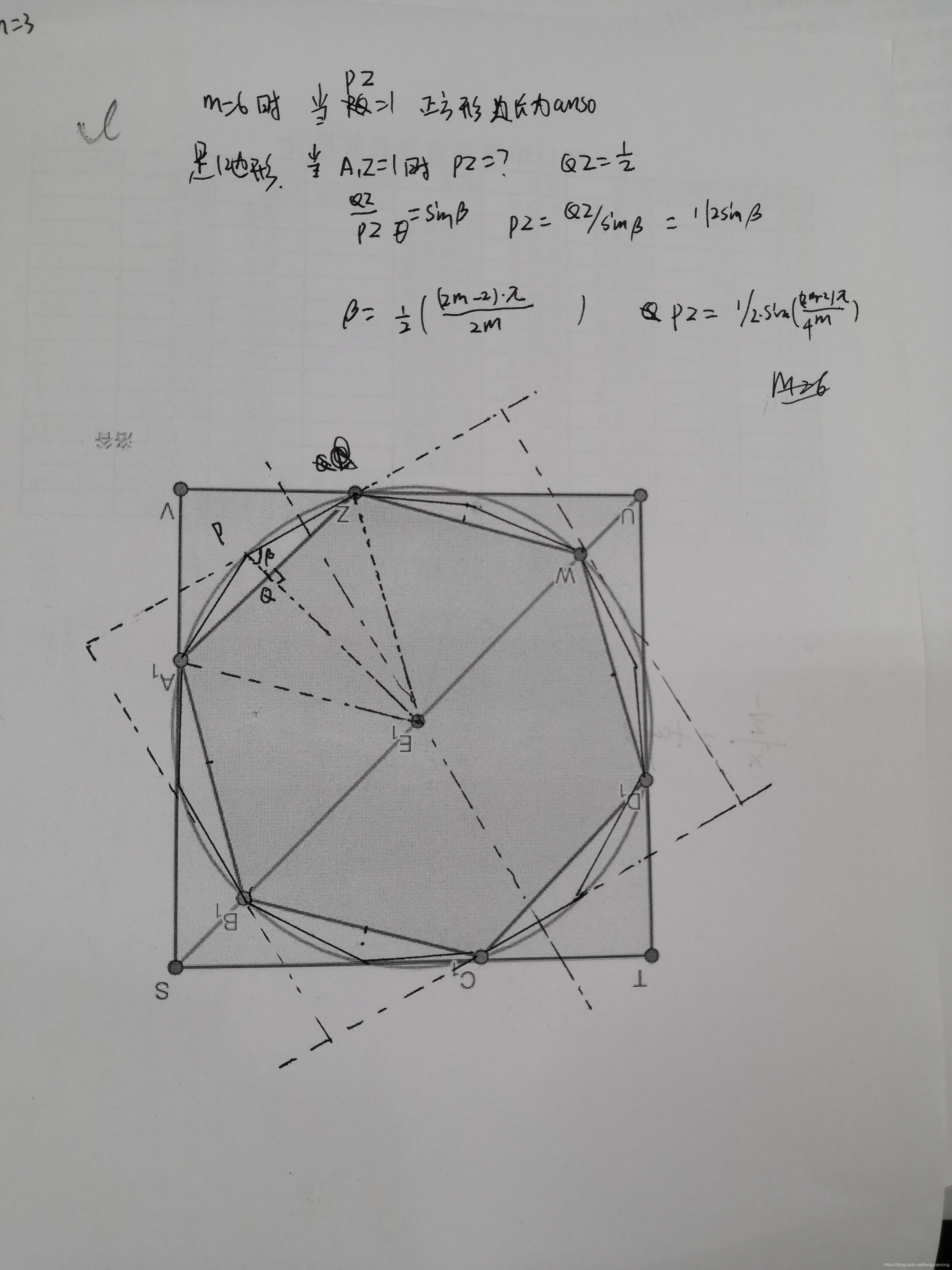
C2这个题目,可以在C1的基础上,将原来的奇数*2,变为偶数,就可以用C1的方法求出。但C1求出的是对应偶数边长为1的值,因此还要根据奇数边长为1的条件,计算出对应偶数的边长,然后再累乘。
#include<bits/stdc++.h>
#define pi 3.1415926535
using namespace std;
int t,n,m;//一定有四条边与正方形重合。用tan函数算算即可
int main(){
cin>>t;
cout<<setprecision(6)<<fixed;
while(t--){
cin>>m;
m=m*2;//算偶数边的
n=m*2;
double ans0=tan(pi*(n-2)/2/n);
//把两条边连一条边,回复到奇数边,;重新计算上述偶数边边长。
double ans1=0.5/sin(pi*(m+m-2)/4/m);
cout<<ans0*ans1<<endl;
}
return 0;
}
 CF正多边形外接正方形边长计算
CF正多边形外接正方形边长计算







 本文介绍了解决CF平台上的两个数学题目的算法:一是计算边数为4k的正多边形的外接正方形边长;二是计算边数为4k+2的正多边形的外接正方形边长。通过使用三角函数和反三角函数,结合c++编程语言,给出了解决方案。
本文介绍了解决CF平台上的两个数学题目的算法:一是计算边数为4k的正多边形的外接正方形边长;二是计算边数为4k+2的正多边形的外接正方形边长。通过使用三角函数和反三角函数,结合c++编程语言,给出了解决方案。
















 630
630

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








