为什么中国的数字是四位一进，而西方的是三位一进？

来自：知乎，作者：孟小七 

链接：https://www.zhihu.com/question/24681119/answer/28636631

数字的发明，应该是人类最早的编码文明。

大家好，今天给大家分享一个知乎很有意思的回答：

这是一个很有趣的问题！

首先，回答题主的问题，为什么为什么西方的数位是3位一进，而东方的是4位一进?

原因在于，西方阿拉伯数字系统采用三位分节法，而中文计数系统采用四位分节法。

有关三位分节法用在中文上有多难受，相信在大家学习英语的过程中，对于「如何快速转换中英文数字」，肯定都有很痛的领悟，什么billion million，就不能按照中文这样，百万千万百亿十亿直接说吗，多简单！

到底为什么会有这个区别呢？

三位分节法，是指在表示一个数时，以三个数字为一段，用逗号或空格隔开；而四位分节法，则是以四个数字为一段啦。

以我国GDP为例， 516282.1亿元，用三位分节法写作 516, 282.1 亿元，用四位分节法写作 51, 6282.1 亿元。

试着用三位分节法读英文，「five hundred and sixteen thousand, two hundred and eighty two, point one 」。

再用四位分节法读中文，「五十一万，六千二百八十二点一亿元」

一下子就读出来了对不对？

如果互换一下…….

要深究这种差别，我们得先膜拜一下中国古代劳动人民的智慧了

一、从计数法说起

现在全世界通用的阿拉伯数字，之所以好用，其中有一个很重要的地方，就在于在运算和记录的过程中数字，只涉及「0,1,2,3,4,5,6,7,8,9」这十个数字符号，不同的值的大小只取决于这符号在数字传中占了哪一位。

简而言之，用「符号+位置」，我们就可以表示任意一个数字。这种高效的计数方法，称为「位值计数法」。

但是在人类发展过程中，大部分文明都是由另一种计数法，这种计数法没有一个统一的名称，这种记数法叫做「符值相加计数法」。

这种计数法的特点，就是遇到一个数字，就起一个名字，比如1000就是千，10000就是万，12就是打，这种「遇到一个起一个」计数法，在埃及文明，古希腊文明，古巴比伦文明中都被广泛使用，这种计数法不能利用符号直接表示数字，而是要用已有的名称算出这个数。

一般采用到的方式就是相同的数字连写，所表示的数等于这些数字相加，小数字在大数字的右边，所表示的数等于这些数字相加，写在左边表示这些数字相减。

比如在罗马数字中Ⅷ = 8，Ⅻ = 12，而1,880这个数，要这么长才可以：MDCCCLXXX。看到这种计数法，学法语的小伙伴有没有感到膝盖一痛？

很明显，符值相加记数法：很，难，用。

由于这种计数系统要同时承担记录和运算的压力，没有将两者相对应，而是运算中有记录，记录又依靠运算，导致无论是记录还是运算都十分繁琐。同时，要运算的数字越大，需要命名的数字就越多。

比如，勤劳勇敢的古埃及人是这么表示九十九万九千九百九十九的：

有木有很像麻将......

不过，我大天朝是全世界唯一个位值计数法和符值相加计数法同步出现并发展的国家。

早在商朝，中国就出现了筹算，这是全世界最早的十进制技术系统。

大概长这样：

永乐大典中的数字：七万一千八百廿四

算筹数系是世界上唯一只用一个符号的方向和位置的组合，表示任何十进位数字或分数的系统。

《孙子算经》云：

凡算之法：先识其位，一从十横，百立千僵，千十相望，万百相当

用这套小木棍，我们可以算简单的四则运算，还可以做分数，负数运算，甚至可以解高次方程……

像这样：

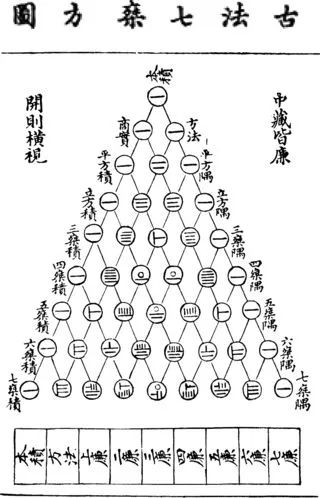
杨辉三角

这套逆天的筹算系统在当时并不用于计数，仅用于运算，计数则采用另一套符值相加计数法的文字系统：个，十，百，千，万，亿……

这两套系统实在是兼容的太过完美，糅合了算筹和文字的新版本也出现了：苏州码子，俗称花码。

一一对应关系

神探夏洛克里也有出现哦：

神探夏洛克 S1E02 算筹和花码

由于机智的老祖宗把命名和运算分割成了两个系统，这样对于中文来说，个十百千万 ，是搭配算筹的「单位」或者说像「占位符」，本身不参与运算，而我们在记录数字的时候，其实只是在做一件事：把算筹系统中十进位制的每一位都起一个名字，而已。

但是在西方，位值计数法这种高级系统，可比中国晚出现了一千多年，在此之前他们一直采用位值命名的方法计数。

中西方不同的计数系统，衍生出的就是两种不同的命名思想：

中国：哇，数字又变大了，我来给新的数位起个名字吧！

西方：哇，数字又变大了，我之前起好名的那些符号能不能凑出这个新数字呢？

有关这两种计数思想对于三位分节法和四位分节法的影响，可以说既是发展的必然，也是历史的偶然。

二、数字怎么这么大？！

西方的数位分节法的源头，在于古希腊的数学体系，其实希腊的数字系统最开始是山寨Attic 数字系统：

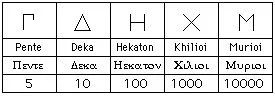
最开始只有5，10，100…等基底。

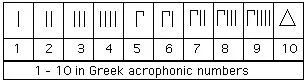
后来发现可以把数字加起来表示1-9：

然后逐渐发展大数系统：

在山寨的基础上，希腊人也开始摸索创立自己的计数系统，但是由于没有位值得概念，可爱呆萌的古希腊银想了一个十分……「妙」的计数法——照搬字母表：

希腊字母和对应的数值

为什么说希腊人可爱呢，因为他们抄字母表的时候，忽然发现：

咦，24个希腊字母不够用了！

于是就把三个废弃的希腊字母（Digamma，Koppa，Sampi）又重新拿出来凑数了，哈哈哈~

可惜就算把废弃的字母都拉出来，表示到「千」的时候还是不够用啊，这可怎么办捏……

他们只好这么做了：

要表达1,000至999,999的数字，就把个位的1-9千加个分隔符表示千，就像这样：

最开始的千

后来发展为这样：

这种下标分隔的形式，可以说是数字分节符的起源。

所以古希腊人的千位数长这样：

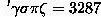
本来呢，呆萌的希腊人觉得千位加个数标凑活用就得了呗，结果发现还有更大的数字，可是字母表都用完了啊肿么办？

于是他们就又重新把Attic数字里表示万的单位M山寨过来，和希腊字母结合表示大数：

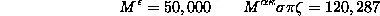
我们可以看到，希腊数系（由于当初凑活用分隔符表示千）采用了四位分节法，大数系统是「希腊特色的Attic（丑到哭）数字」，但这种数字分节的思想影响深远。

而希腊文之后的拉丁文，也是采用相似的字母计数法，只不过字母变成了罗马字母而已：

Ⅰ  1   unus

Ⅱ  2   duo

Ⅲ  3   tres

Ⅳ  4   quattuor

Ⅴ  5   quinque

Ⅵ  6   sex

Ⅶ  7   septem

Ⅷ  8   octo

Ⅸ  9   novem

Ⅹ  10  decem

罗马数字的进步之处在于，一个是简化了数字符号，另一个则是引入了「千」的单位：M

罗马人本来是山寨了希腊字母来表示千，后来还用过很多奇怪的方法，最终固定的M来源于拉丁文mile,意为一千。

我们可以看出，罗马文化是深受希腊文化影响的，但是为什么没有把希腊数当作「万」呢？

我的推测，首先希腊人大写加上标的表示方法和罗马的纯字母体系不相符，也就是说，「不符合罗马人的设计美学」；其次估计他们也是抱着「最开始用不到」的心态，后面发现数字越来越大，只好在数字上加一横表示这个数乘1000，因为彼时希腊的M和罗马的M已经撞车，山寨不了万的单位了……于是就这么着吧……三位分节法就这样定下来了……

又过了很久很久，印度的数字系统被阿拉伯人改造并引入西方，西方有了真正的位值计数法的计数系统，数学研究突飞猛进,。这已经是很久以后的故事了。

三、我大天朝，打仗要紧

说完西方三位分节的起源，再回过头看看为什么中国人采用了四位分节。

前面说到了，中国的计数系统不必承担运算的压力，可以一心一意计数，而算筹体系早在商朝就有出现。

我们首先看商朝的人口，根据殷商卜辞中的甲骨文可以知道，商朝当时征兵是以千为单位，计量土地也是在井田制度的基础上，以亩搭配尺作为单位，在运算过程中并不涉及到万以上的单位。

可考文献：

王登人五千征土方（《殷虚书契后编》上．31．5）

不过，此时大城市，也就是邑，人数已经到达十万规模了。（此处可根据商朝的井田制推算出大致人口），而到周礼中，征兵人数也没有过万，也就是说，万这个单位，商周已经固定下来。

前面说过，中国的计数逻辑是「有了更高的数位就起个新名字」，不过五经算数有记载「按黄帝为法，数有十等。及其用也，乃有三焉。十等者，谓“亿、兆、京、垓、秭、壤、沟、涧、正、载”也。三等者，谓“上、中、下”也。其下数者，十十变之。若言十万曰亿，十亿曰兆，十兆曰京也。中数者，万万变之。若言万万曰亿，万万亿曰兆，万万兆曰京也。上数者，数穷则变。若言万万曰亿，亿亿曰兆、兆兆曰京也。」

这种说法到底对不对呢？

我们可以看到，到周朝的时候，最大的计数单位都是到「亿」为止，而「兆」当时只有占卜的意义，中国的大数系统发展起来，应该是春秋战国时期的故事啦，有关黄帝创立大数系统，应该是传说。

亿丧贝。——《易·震》

大卜掌三兆之法,一曰玉兆,二曰瓦兆,三曰原兆——――《周礼·大卜》

《诗经》“丰年”篇有“万亿及秭”之说 ，“亿”“秭”就是两个大数名。毛苌注进一步解释 ：“数万至万日亿 ，数亿至万 日秭 。”就是说 ：“亿”等于一万万 ，跟今天最常用的大数“亿”一样 ；“秭”等于一万亿 ，应该是 由亿逐次 (十 )进位而得 。

因此，至公元 3世纪，事实上已存在有十进和万进两种大数记数法 。南北朝时期 ，我国的大数记法有 了进一步的发展 ，出现了以亿 、兆、京、垓 、秭、壤 、沟、涧、正 、载十个字为基础的大数名词系统。

殷人最重要的就是打仗，祭祀，这两件事都不需要动用万以上的数字，既然用不到，就没有这个意识，以后万进制和亿进制的大数系统也就是在商朝的基础上添加罢了，因为到这么大的数字，运算依旧要依靠算筹，那么从万开始分节，运算完毕只要把单位加上万即可，方便省事。

中国的计数历史从商朝算起，不过大数系统发展比较混乱，由于终究要依靠商朝流传的算筹进行运算，最终留下来的是四位分节的形式。

四、我们有了位值计数法！

当海那边的西方友人被阿拉伯数字的方便惊叹时，却发现了一个问题：阿拉伯数字好用是好用，可是有一个问题：太长啦！

比如：100000000000000，到底是多少一眼根本看不清啊！

由于不像中国，一直有一套独立的数字命名系统，所以西方的数学家只好从他们的老祖宗那里找办法，直到13世纪的法国，数学界才根据拉丁文mile延伸出million（mile one）,billion (bi-million)等词语，以表示更大的数值。

而对于大数字，为了方便阅读，则是借鉴了古希腊「下标分节」的计数法，只不过古希腊没有零的概念，所以直接加占位符，现在中间的三位用零占位。

归根结底，之所以西方习惯用三位分节法而不用四节分位法表示数字，根本原因在于：

古希腊人的字母表不够用了。

其实古希腊人并且也使用四位分节法，而且有专门表示万的词语，不过罗马人罗马人把它们丢掉了...丢...掉...了....，以后读不对英文数字的时候，请撸起袖子，亮出你的罗马表...

有同学问怎么做到快速转换，我有一个方法，大家不妨一试：

以下是手写的转换过程...

大概说一下怎么操作：

1.用阿拉伯数字计数

2.当原语开始读到第一个计数单位时，找到离目标语言最近的分节点，并标号（最好标出单位）

3.之后听到的数字不计单位只计数，按照目标语言的分节方式分节

4.在分节点加上目标语言的计数单位

比如五千零四十三亿，听到四十三亿，反映到英文中十亿是billion，于是先记下5043，再在十亿对应的四后面分节，504'3

five hundred and four billion 听到billion，反映到中文中下一位就是亿，于是记下504，留一个空位，再分节 504   '

重点在于第一步，找到目标语言的最近分节点，然后就很简单啦~

-------- End --------
图解Pandas图文00-内容框架介绍图文01-数据结构介绍图文02-创建数据对象图文03-操作Excel文件图文04-常见的数据访问图文05-常见的数据运算图文06-常见的数学计算图文07-常见的数据统计图文08-常见的数据筛选图文09-常见的缺失值处理图文10-数据合并操作