Matlab 基于Music算法的时序信号频率估计：解锁电力系统奥秘-优快云博客

Matlab 基于Music算法的时序信号频率估计可用于其他频率估计方法对比可用于电力系统中谐波，突变检测

在信号处理的广袤领域中，频率估计是一项关键任务，尤其在电力系统等诸多应用场景里，精准的频率估计意义重大。今天咱们就来唠唠基于Music算法的时序信号频率估计，这可是个在Matlab中施展身手的好方法，还能和其他频率估计方法一较高下，在电力系统谐波与突变检测方面大显神通。

Music算法原理小探

Music算法，全称为Multiple Signal Classification，它主要是利用信号子空间和噪声子空间的正交性来实现频率估计。假设有一个由多个正弦信号组成的时序信号，其数学模型可表示为：

\[ x(n) = \sum{i = 1}^{p} ai e^{j2\pi f_i n} + w(n) \]

这里\( p \)是信号源的个数，\( ai \)是第\( i \)个信号的幅度，\( fi \)是对应的频率，\( w(n) \)就是噪声啦。通过对信号的协方差矩阵进行特征分解，就能把信号子空间和噪声子空间区分开。然后利用这两个子空间的正交特性，构造出Music谱，谱峰对应的频率就是我们要找的信号频率。

Matlab代码实战

% 参数设置
fs = 1000; % 采样频率
t = 0:1/fs:1 - 1/fs; % 时间向量
f1 = 50; f2 = 120; % 两个正弦信号频率
x = 2*cos(2*pi*f1*t) + 3*cos(2*pi*f2*t); % 合成信号
N = length(x); % 信号长度

% 计算协方差矩阵
Rxx = xcorr(x)/N;
Rx = toeplitz(Rxx(1:N));

% 特征分解
[V,D] = eig(Rx);
eigenvalues = diag(D);
[eigenvalues_sorted,index] = sort(eigenvalues,'descend');
V = V(:,index);

% 信号和噪声子空间划分
p = 2; % 信号源个数
Es = V(:,1:p); % 信号子空间
En = V(:,(p + 1):end); % 噪声子空间

% Music谱计算
f = 0:0.01:fs/2;
Pmusic = zeros(size(f));
for i = 1:length(f)
    a = exp(-j*2*pi*f(i)*(0:N - 1)');
    Pmusic(i) = 1/(a'*En*En'*a);
end

% 绘图
figure;
plot(f,10*log10(Pmusic/max(Pmusic)));
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title('MUSIC Spectrum');
grid on;

代码分析

参数设置与信号合成：首先定义了采样频率\( fs \)、时间向量\( t \)，以及两个正弦信号的频率\( f1 \)和\( f2 \)，并合成了一个混合信号\( x \)。这就像是搭建一个小的信号“舞台”，为后续操作做准备。
协方差矩阵计算：通过\( xcorr \)函数计算信号的自相关函数，并归一化得到协方差矩阵\( Rx \)。协方差矩阵包含了信号的很多关键信息，就像一个宝藏盒，等着我们进一步挖掘。
特征分解：对协方差矩阵\( Rx \)进行特征分解，得到特征向量矩阵\( V \)和特征值矩阵\( D \)。然后将特征值按从大到小排序，并相应地调整特征向量的顺序。特征分解是Music算法的关键步骤，就像是把宝藏盒里的东西分类摆放好，便于后续挑选。
子空间划分：根据已知的信号源个数\( p \)，将特征向量划分为信号子空间\( Es \)和噪声子空间\( En \)。这一步明确了信号和噪声的“领地”，为后续计算Music谱奠定基础。
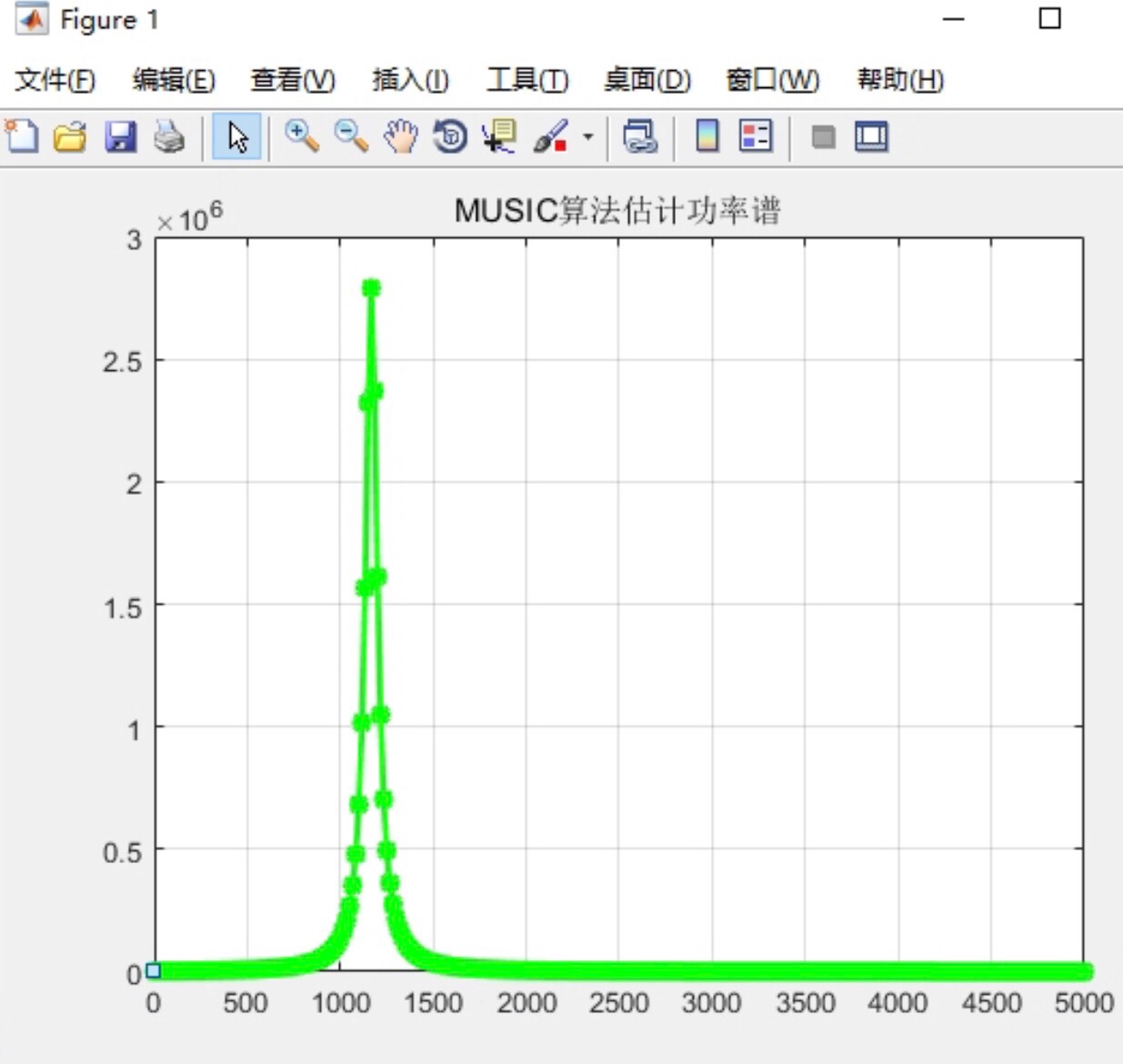
Music谱计算与绘图：在设定的频率范围内，对每个频率点计算Music谱值\( Pmusic \)。这里利用了噪声子空间与信号导向矢量的正交关系。最后绘制出Music谱，从图中就能直观地看到谱峰对应的频率，也就是我们估计出的信号频率。

在电力系统中的应用

谐波检测

在电力系统中，谐波会对设备造成损害，影响电能质量。基于Music算法的频率估计可以精确检测出谐波的频率。比如在复杂的电力信号中，可能存在多个不同频率的谐波成分，Music算法能像敏锐的“猎手”一样，准确找出这些谐波频率，帮助工程师及时采取措施进行谐波治理。

突变检测

当电力系统发生故障或其他突变情况时，信号的频率可能会瞬间改变。Music算法凭借其对频率变化的敏感捕捉能力，能够快速检测到这种突变。一旦检测到突变，系统可以迅速做出响应，采取保护措施，保障电力系统的稳定运行。

与其他频率估计方法对比

和传统的周期图法相比，Music算法在低信噪比情况下表现更为出色。周期图法虽然简单直接，但容易受到噪声干扰，估计精度不高。而Music算法利用子空间特性，能有效抑制噪声影响，提供更准确的频率估计。和Capon算法相比，Music算法在多信号源情况下，频率分辨能力更强，能够更清晰地分辨出不同频率的信号。

总之，基于Music算法的时序信号频率估计在Matlab中是一个强大的工具，无论是在理论研究还是实际应用，尤其是电力系统领域，都有着巨大的潜力。希望通过这篇博文，能让大家对它有更深入的了解和认识，在自己的项目中充分发挥它的优势。