列车-钢弹簧浮置板-轨道耦合垂向时域程序 根据《车辆-轨道耦合动力学》编写 Matlab代码 ...

列车-钢弹簧浮置板-轨道耦合垂向时域程序 根据《车辆-轨道耦合动力学》编写 Matlab代码 注：仅售代码，如需，需要有偿询问。

深夜的实验室键盘声此起彼伏，显示器上跳动的曲线让我突然想起三年前调不通浮置板模型的抓狂经历。钢弹簧浮置板这玩意就像给轨道铺了层席梦思床垫，但要让数学方程和代码真正"睡"在这床垫上可不容易。今天咱们就扒开这个耦合模型的代码骨架，看看它怎么在时域里蹦迪。

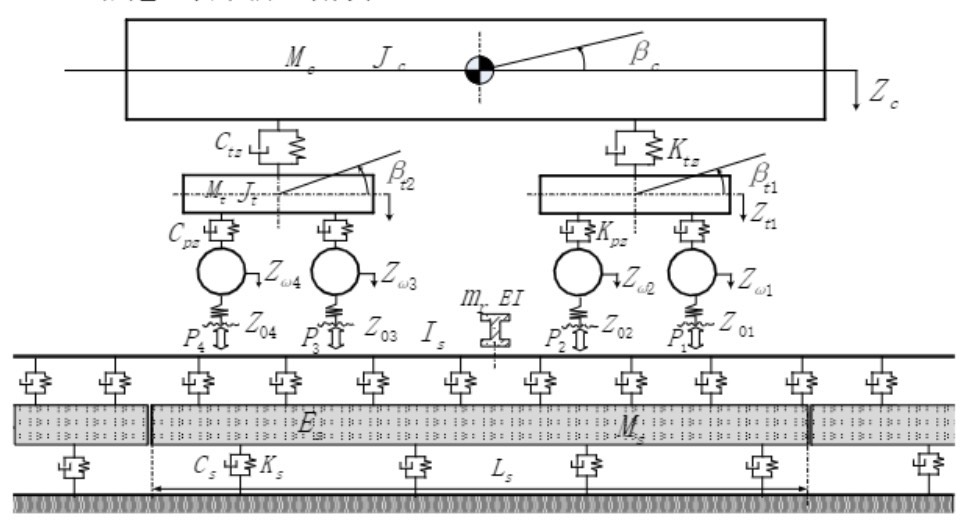
先看模型的三板斧：车辆用多刚体建模，轨道用Euler梁，中间夹着非线性钢弹簧阻尼元件。Matlab代码里最带劲的是这个状态变量拼接：

state = [Z_vehicle; dZ_vehicle; Y_rail; dY_rail; F_spring];

这里把车辆位移速度、轨道位移速度、弹簧力打包成375维的超级向量——别数了，光车轮子就挂了32个自由度，轨道节点更是直接飙到200+。

微分方程核心在计算轮轨力这块，伪代码长这样：

function dstate = dynamics(t, state)
    % 解包状态变量
    [vehicle_pos, vehicle_vel, rail_pos, rail_vel, spring_force] = unpack(state);
    
    % 轮轨接触计算
    wheel_gap = vehicle_pos - rail_pos(contact_nodes);
    normal_force = max(0, 1e8 * wheel_gap);  % 非线性接触刚度
    
    % 钢弹簧迟滞特性
    spring_rate = 5e6 + 3e4 * tanh(spring_force/1e4);  //伪代码，实际用微分方程描述
    
    % 组装微分方程组
    d_vehicle = M_vehicle \ (normal_force - C_vehicle*vehicle_vel);
    d_rail = K_rail * rail_pos + damping_term;
    d_spring = hysteresis_model(spring_rate, rail_vel);
    
    dstate = [vehicle_vel; d_vehicle; rail_vel; d_rail; d_spring];
end

特别注意第7行的tanh函数，这里用光滑函数模拟了钢弹簧刚度随载荷变化的特性，比论文里生硬的折线模型更带感。

求解器用ode45可能会被刚度矩阵虐哭，实测换成ode15s后运算速度从乌龟爬进化到兔子跳。记得设置最大步长不超过Δt=0.001s，否则高频振动会直接糊成马赛克。

最后来点可视化魔法：

subplot(3,1,1);
plot(t_hist, F_wheel);  % 轮轨力跳探戈
title('轮轨力时程曲线 - 这振幅够开夜店了');

subplot(3,1,2);
surf(node_position, t_hist, rail_deform);  % 轨道变形曲面
shading interp;  % 让波纹像水一样流动

subplot(3,1,3);
hysteresis_loop = plot(spring_deform(1:end-1), spring_force_diff);  % 滞回曲线
set(hysteresis_loop, 'Color', [0.8 0.2 0.6]);  % 基佬紫的力学美

跑完程序盯着这三张图，你会明白为啥地铁经过时楼板会哆嗦——那些扭成麻花的滞回曲线，分明是钢弹簧在疯狂diss振动能量。

想要魔改模型？试试把第13行的线性阻尼换成磁流变阻尼器模型，保证微分方程立马表演暴走。不过记得备好咖啡，刚度矩阵的迭代校正绝对能让你的CPU闻到焦香。