向量可以平移,向量模长与方向确定也不唯一
向量使矢量,既有大小又有方向
数量积:
a⃗⋅b⃗=∣a⃗∣∗∣b⃗∣∗cosθa⃗⋅b⃗=x1y1+x2y2+⋯+xnyn\vec a \cdot \vec b = |\vec a|*|\vec b|*cos\theta \\ \vec a \cdot \vec b=x_1y_1 + x_2y_2 + \cdots + x_ny_n a⋅b=∣a∣∗∣b∣∗cosθa⋅b=x1y1+x2y2+⋯+xnyn
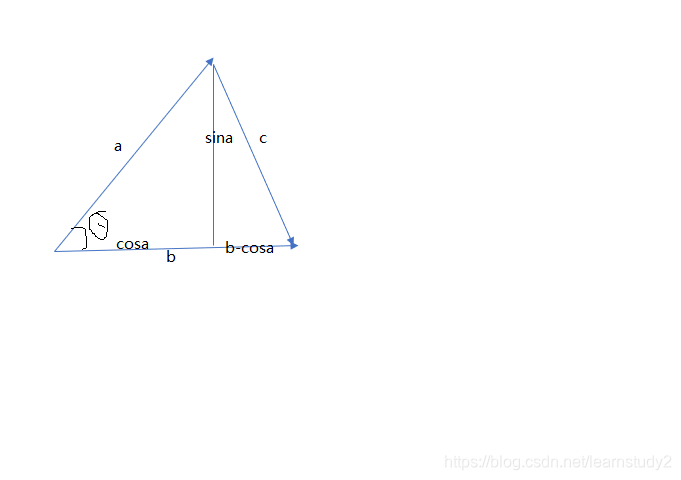
∣c⃗∣2=(∣a⃗∣sinθ)2+(∣b⃗∣−∣a⃗∣cosθ)2∣c⃗∣2=∣a⃗∣2sin2θ+∣b⃗∣2−2∣b⃗∣∣a⃗∣cosθ+∣a⃗∣2cos2θ∣c⃗∣2=∣a⃗∣2(sin2θ+cos2θ)+∣b⃗∣2−2∣b⃗∣∣a⃗∣cosθsin2θ+cos2θ=1∣c⃗∣2=∣a⃗∣2+∣b⃗∣2−2∣b⃗∣∣a⃗∣cosθ
|\vec c|^2 = (|\vec a|sin\theta)^2 + (|\vec b|-|\vec a|cos\theta)^2 \\
|\vec c|^2 = |\vec a|^2sin^2\theta + |\vec b|^2 -2|\vec b||\vec a|cos\theta + |\vec a|^2cos^2\theta \\
|\vec c|^2 = |\vec a|^2(sin^2\theta + cos^2\theta) + |\vec b|^2 -2|\vec b||\vec a|cos\theta \\
sin^2\theta + cos^2\theta = 1 \\
|\vec c|^2 = |\vec a|^2 + |\vec b|^2 - 2|\vec b||\vec a|cos\theta \\
∣c∣2=(∣a∣sinθ)2+(∣b∣−∣a∣cosθ)2∣c∣2=∣a∣2sin2θ+∣b∣2−2∣b∣∣a∣cosθ+∣a∣2cos2θ∣c∣2=∣a∣2(sin2θ+cos2θ)+∣b∣2−2∣b∣∣a∣cosθsin2θ+cos2θ=1∣c∣2=∣a∣2+∣b∣2−2∣b∣∣a∣cosθ
坐标表示:c⃗=a⃗−b⃗a⃗−b⃗=(x1−x2,y1−y2)∣c⃗∣2=(x1−x2)2+(y1−y2)2∣a⃗∣2=x12+y12∣b⃗∣2=x22+y22
\vec c = \vec a - \vec b \\
\vec a - \vec b = (x_1-x_2,y_1-y_2) \\
|\vec c|^2 = (x_1-x_2)^2 + (y_1-y_2)^2 \\
|\vec a|^2 = x_1^2 + y_1^2 \\
|\vec b|^2 = x_2^2 + y_2^2 \\
c=a−ba−b=(x1−x2,y1−y2)∣c∣2=(x1−x2)2+(y1−y2)2∣a∣2=x12+y12∣b∣2=x22+y22∣c⃗∣2=∣a⃗∣2+∣b⃗∣2−2∣b⃗∣∣a⃗∣cosθ(x1−x2)2+(y1−y2)2=x12+y12+x22+y22−2∣b⃗∣∣a⃗∣cosθx12−2x1x2+x22+y12−2y1y2+y22=x12+y12+x22+y22−2∣b⃗∣∣a⃗∣cosθx12−2x1x2+x22+y12−2y1y2+y22=x12+y12+x22+y22−2∣b⃗∣∣a⃗∣cosθ−2x1x2−2y1y2+=−2∣b⃗∣∣a⃗∣cosθ2x1x2+2y1y2=2∣b⃗∣∣a⃗∣cosθx1x2+y1y2=∣b⃗∣∣a⃗∣cosθ∣b⃗∣∣a⃗∣cosθ=x1x2+y1y2
|\vec c|^2 = |\vec a|^2 + |\vec b|^2 - 2|\vec b||\vec a|cos\theta \\
(x_1-x_2)^2 + (y_1-y_2)^2 = x_1^2 + y_1^2 + x_2^2 + y_2^2 - 2|\vec b||\vec a|cos\theta \\
x_1^2 - 2x_1x_2 + x_2^2 + y_1^2 - 2y_1y_2 + y_2^2 = x_1^2 + y_1^2 + x_2^2 + y_2^2 - 2|\vec b||\vec a|cos\theta \\
\bcancel x_1^2 - 2x_1x_2 + \bcancel x_2^2 + \bcancel y_1^2 - 2y_1y_2 + \bcancel y_2^2 =\bcancel x_1^2 +\bcancel y_1^2 +\bcancel x_2^2 +\bcancel y_2^2 - 2|\vec b||\vec a|cos\theta \\ - 2x_1x_2 - 2y_1y_2 + = - 2|\vec b||\vec a|cos\theta \\
2x_1x_2 + 2y_1y_2 = 2|\vec b||\vec a|cos\theta \\
x_1x_2 + y_1y_2 = |\vec b||\vec a|cos\theta \\
|\vec b||\vec a|cos\theta = x_1x_2 + y_1y_2
∣c∣2=∣a∣2+∣b∣2−2∣b∣∣a∣cosθ(x1−x2)2+(y1−y2)2=x12+y12+x22+y22−2∣b∣∣a∣cosθx12−2x1x2+x22+y12−2y1y2+y22=x12+y12+x22+y22−2∣b∣∣a∣cosθx12−2x1x2+x22+y12−2y1y2+y22=x12+y12+x22+y22−2∣b∣∣a∣cosθ−2x1x2−2y1y2+=−2∣b∣∣a∣cosθ2x1x2+2y1y2=2∣b∣∣a∣cosθx1x2+y1y2=∣b∣∣a∣cosθ∣b∣∣a∣cosθ=x1x2+y1y2
a⃗⋅b⃗=∣a⃗∣∗∣b⃗∣∗cosθ∣b⃗∣∣a⃗∣cosθ=x1x2+y1y2a⃗⋅b⃗=x1x2+y1y2 \vec a \cdot \vec b = |\vec a|*|\vec b|*cos\theta \\ |\vec b||\vec a|cos\theta = x_1x_2 + y_1y_2 \\ \vec a \cdot \vec b =x_1x_2 + y_1y_2 a⋅b=∣a∣∗∣b∣∗cosθ∣b∣∣a∣cosθ=x1x2+y1y2a⋅b=x1x2+y1y2
向量积
∣a⃗×b⃗∣=∣a⃗∣∗∣b⃗∣∗sinθ|\vec a \times \vec b| = |\vec a|*|\vec b|*sin\theta ∣a×b∣=∣a∣∗∣b∣∗sinθ
矩阵
矩阵,即描述线性代数中线性关系的参数,即矩阵是一个线性变换,可以将一些变量转换为另一些向量
矩阵是向量的集合




 本文深入探讨了向量的基本属性,包括其平移特性、模长与方向的确定性,以及向量作为矢量的性质。详细解析了向量的数量积与向量积公式,展示了如何通过坐标表示进行向量运算。同时,文章引入了矩阵的概念,阐述了矩阵在线性代数中的作用,即通过线性变换将一组变量转化为另一组向量。
本文深入探讨了向量的基本属性,包括其平移特性、模长与方向的确定性,以及向量作为矢量的性质。详细解析了向量的数量积与向量积公式,展示了如何通过坐标表示进行向量运算。同时,文章引入了矩阵的概念,阐述了矩阵在线性代数中的作用,即通过线性变换将一组变量转化为另一组向量。
















 2338
2338

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








