1位全加法器单位延时

最新推荐文章于 2023-12-18 10:35:33 发布

原创最新推荐文章于 2023-12-18 10:35:33 发布 · 562 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#程序人生

该实验详细介绍了使用Verilog HDL设计和仿真1位全加法器的过程，通过单位延时展示信号动作的时间顺序。实验涉及Add_full_unit_delay和Add_half_unit_delay两个模块，以及相应的测试代码。在Modelsim软件中完成编译和仿真，观察并理解信号的变化。

一，实验内容
Verilog HDL高级数字设计（第二版）P80页例题4.8实验1位全加法器单位延时的仿真
在这里插入图片描述

二，实验目的
能够采用单位延时能够显示信号动作的时间顺序

三，实验代码
module Add_full_unit_delay(output c_out,sum,input a,b,c_in);
wire w1,w2,w3;
Add_half_unit_delay M1(w2,w1,a,b);
Add_half_unit_delay M2(w3,sum,w1,c_in);
or #1 M3(c_out,w2,w3);
endmodule
module Add_half_unit_delay (output c_out,sum,input a,b);
xor #1 M1(sum,a,b);
and #1 M2(c_out,a,b);
endmodule

module Add_half_unit_delay (output c_out,sum,input a,b);
xor #1 M1(sum,a,b);
and #1 M2(c_out,a,b);
endmodule

测试代码
module tb_Add_full_unit_delay();
reg a, b, c_in;
wire sum, c_out;

Add_full_unit_delay fulladd(.c_out(c_out),.sum(sum),.a(a),.b(b),.c_in(c_in));

initial
begin
a=1’b0;b=1’b0;c_in=1’b0;
#5 a=1’b0;b=1’b0;c_in=1’b0;
#5 a=1’b0;b=1’b1;c_in=1’b0;
#5 a=1’b1;b=1’b1;c_in=1’b0;
#5 a=1’b1;b=1’b0;c_in=1’b0;
#5 a=1’b0;b=1’b0;c_in=1’b1;
#5 a=1’b0;b=1’b1;c_in=1’b1;
#5 a=1’b1;b=1’b1;c_in=1’b1;
#5 a=1’b1;b=1’b0;c_in=1’b1;
#20 $stop;
end

endmodule

四，实验过程
1.打开modelsim软件
2.选择文件file,新建new,工程project，如图
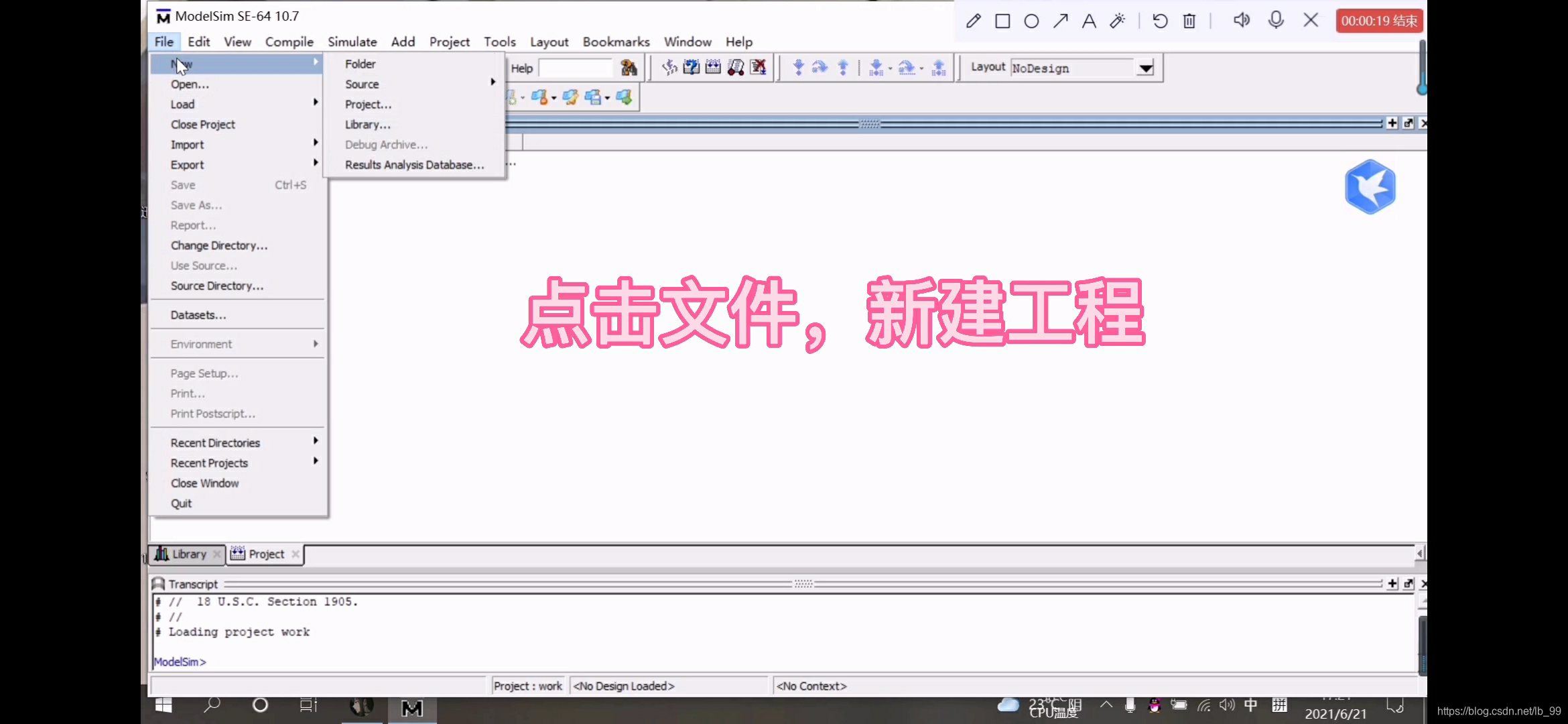
在这里插入图片描述

3.接着会弹出这个对话框，命名为“work”,点击“OK”，如图
在这里插入图片描述

4.选择创造一个新文件（Create New File）把文件名输入到对话框中“Add_full_unit_delay”,选择仿真途径为Verilog，点击“OK”，关闭对话框，如图
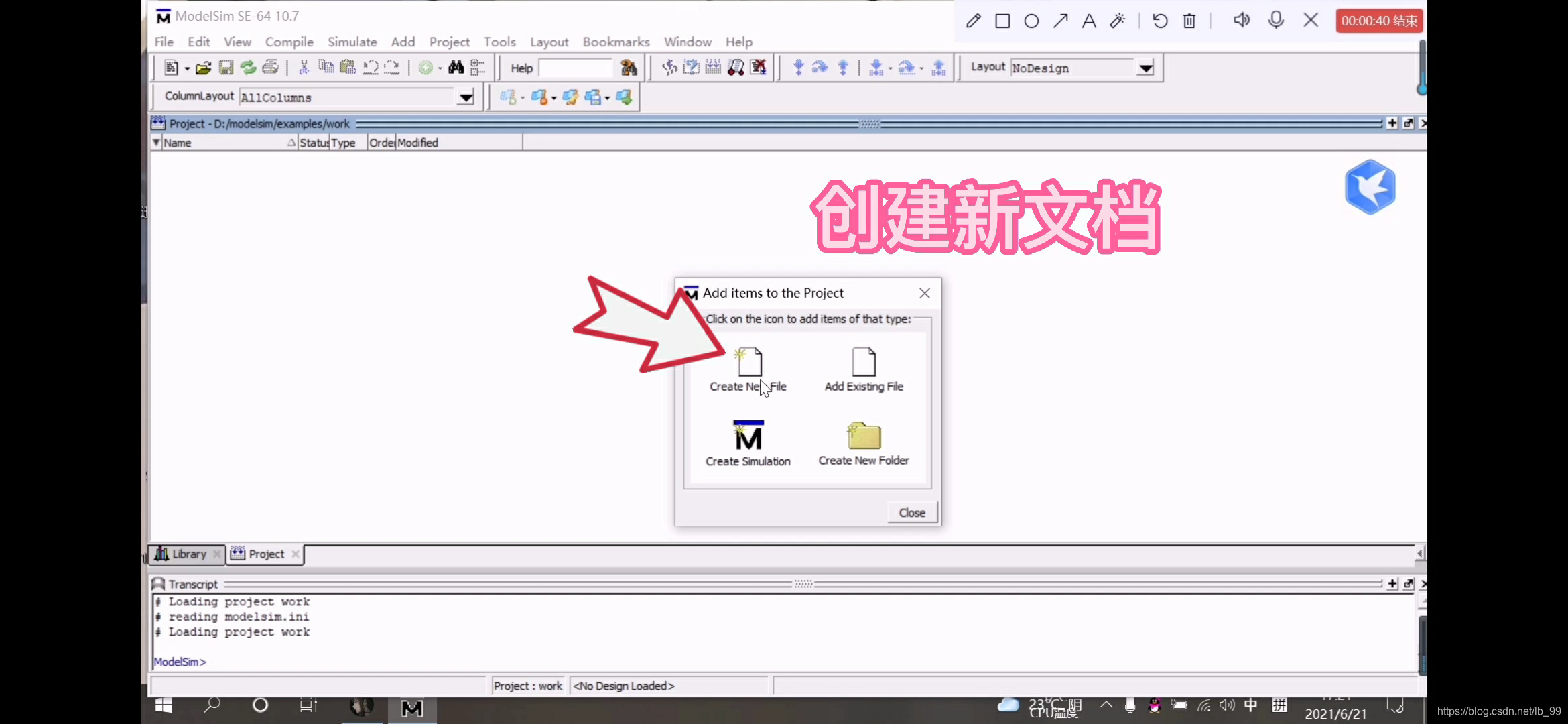
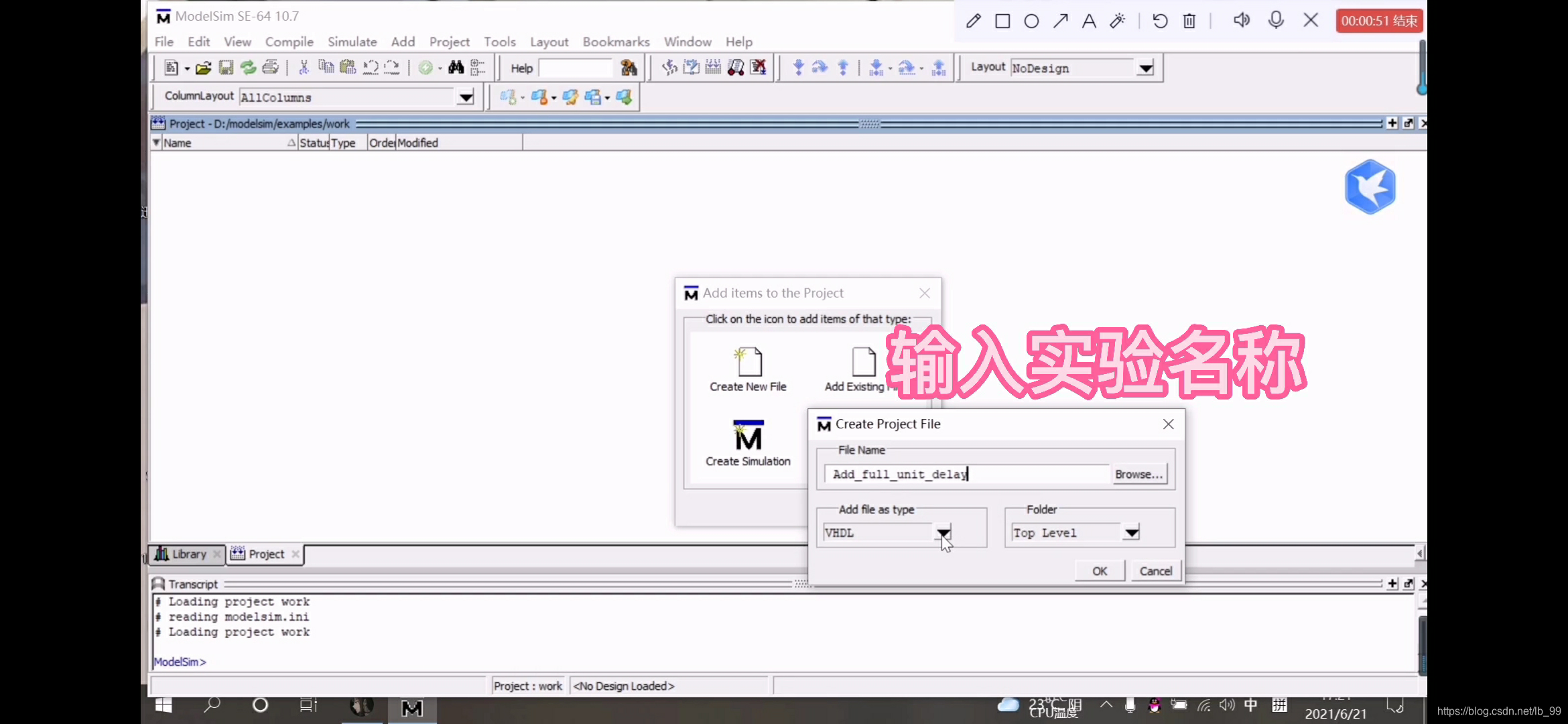
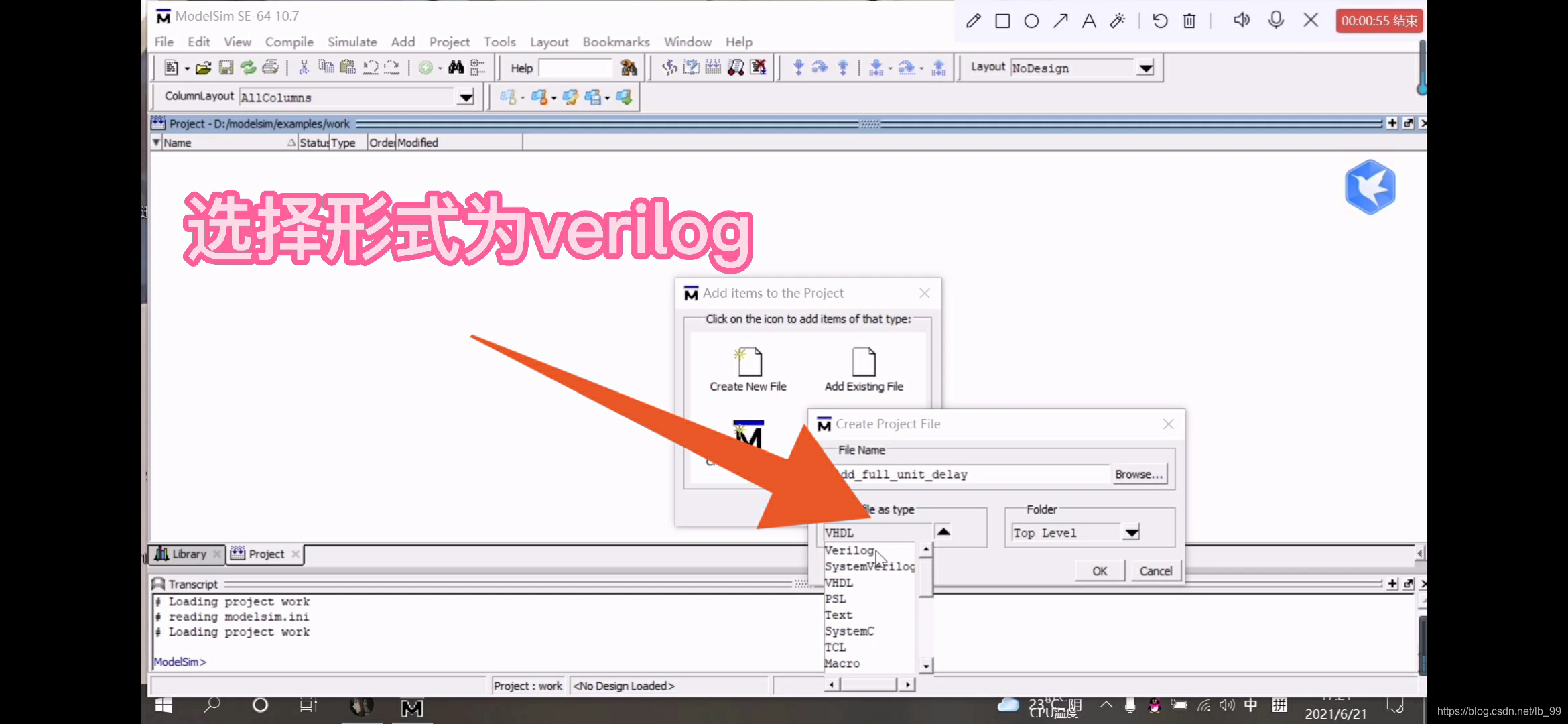
在这里插入图片描述

5.双击文件，输入代码，剩余的两个文件进行一样的操作，如图
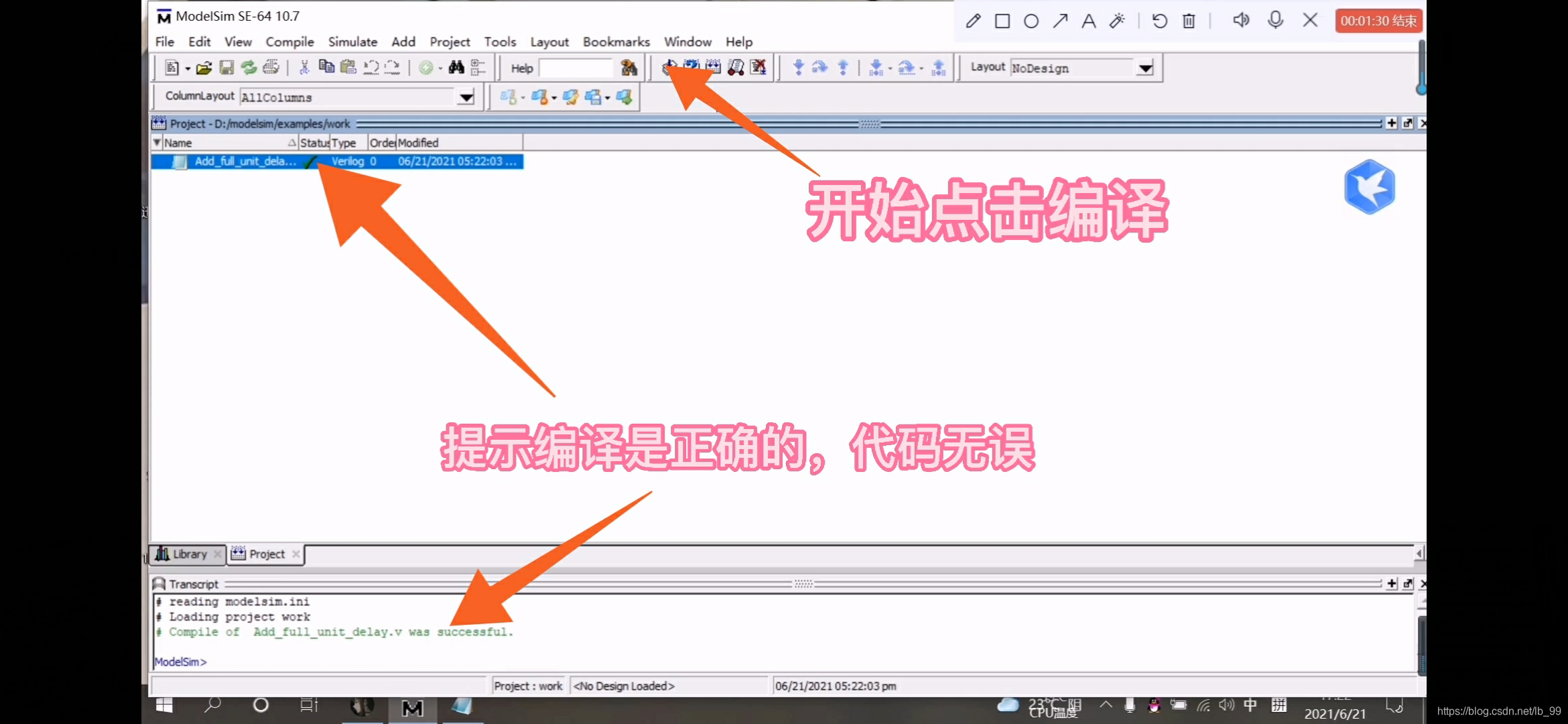
在这里插入图片描述

6.保存代码后，开始进行编译，看代码是否错误，点击菜单栏中的编译按钮“compile”,如图
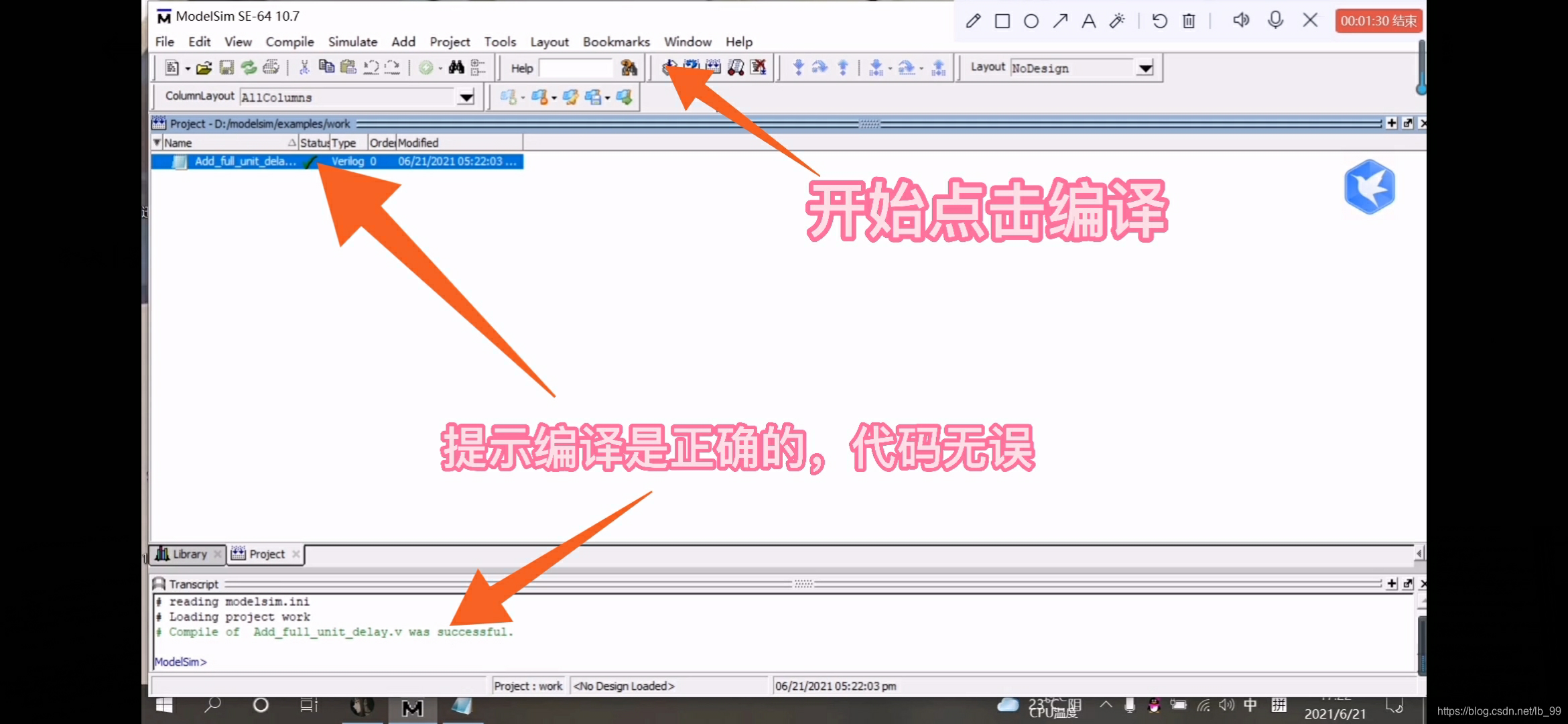
在这里插入图片描述

7.编译后，如果代码正确，左下角就会出现绿色的提示；反之，就会是红色的警告，接着就开始仿真，点击菜单栏中的仿真按钮“simulate”,如图
在这里插入图片描述

8.点击仿真后，会出现如下对话框，找到创建的文件work,选择要编译的文件Add_full_unit_delay,点击OK，如图
在这里插入图片描述

9.编译成功后，选择测试文件，点击右键，选择添加波形Add Wave，如图
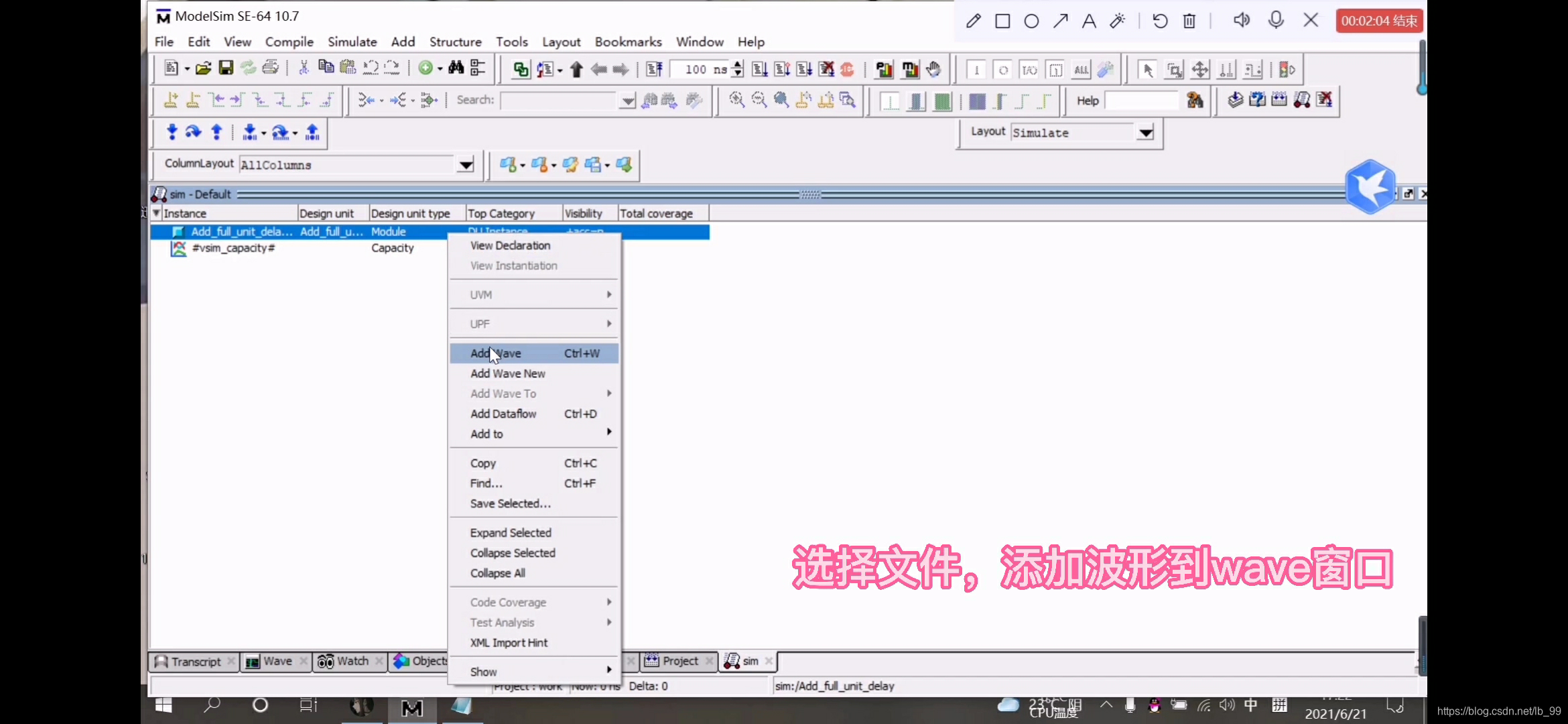
在这里插入图片描述

10.点击Run-ALL，点击OK，如图
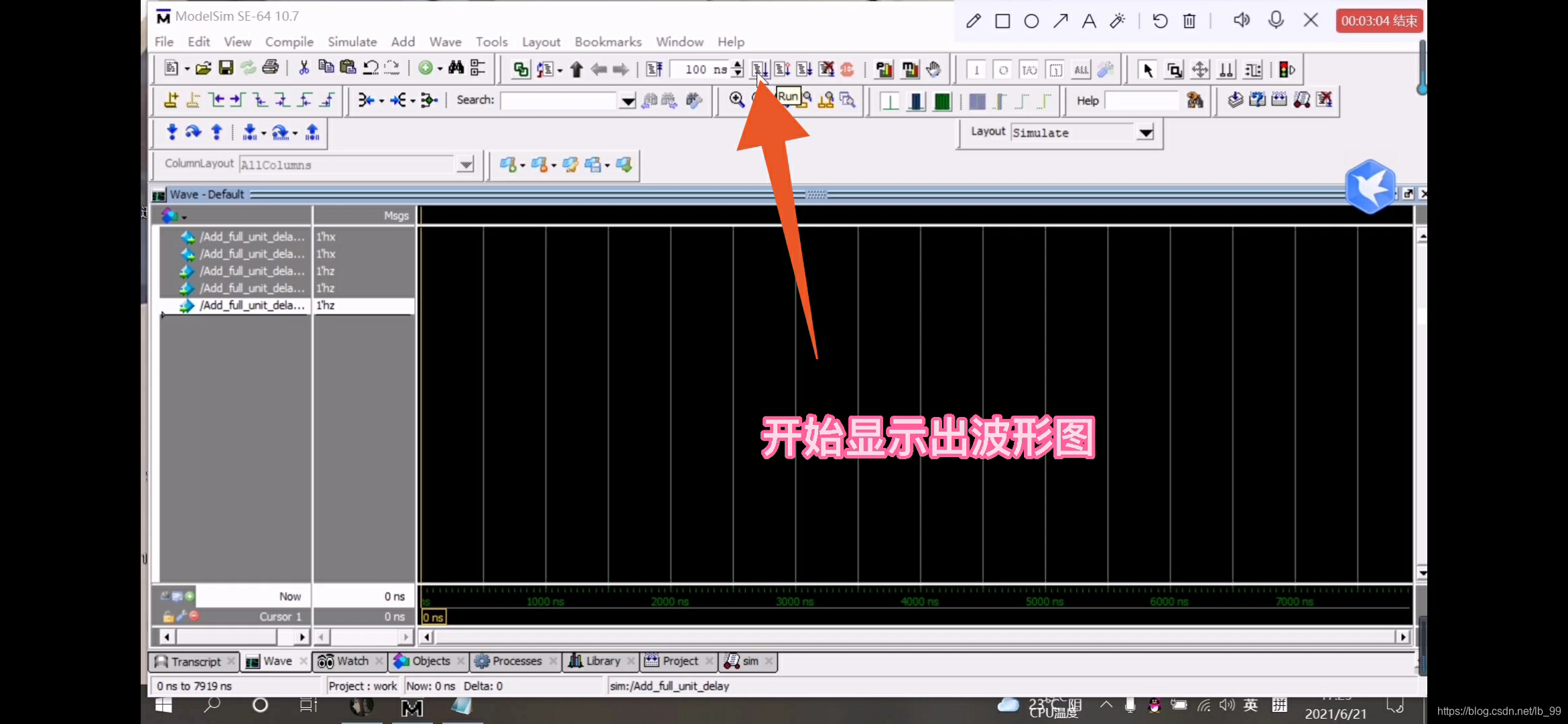
在这里插入图片描述

11.实验截屏

五，实验视频
链接：https://www.bilibili.com/video/BV1eb4y1C7Kr?share_source=copy_web

欢迎前往哔哩哔哩观看视频讲解