Coursera-Machine Learning-ex4

Some Points:

Implement Steps:

1.Pick a neural network  architecture.

• number of input units = dimension of features
• number of output units = number of classes
• number of hidden layer = 1(Default), if you have more than 1 hidden layer, it recommended that every hidden layer have the same number of units
• number of hidden units per layer = .. Usually the more the better

2. Randomly initialize the weights so that they are not competely identical. Formally says "break symmetry"

3. Implement a for-loop for t = 1: m and place the steps 3.1 - 3.3 below inside the for-loop. With the t-th iteration performing the calculation on the t-th trainng example (x(t), y(t)).

• 3.1 Implement forward propagation to get vector a(unit) and vector z(unit) for each layer.

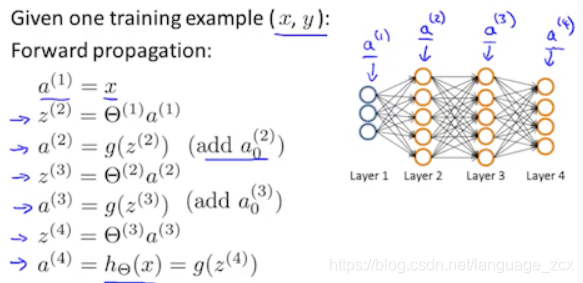
• 3.2 Implement cost function for the t-th example.

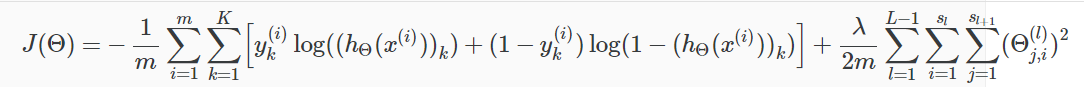
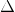• 3.3 Implement back propagation to get vector (unit) and matrix (weight).

4. Get the averages of  cost function and matrix 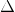,  add regurlarization portion.Attention the index begin at 1,  ignoring the bias units.

5.Use gradient checking to confirm that your backprpa works well.

6. Use  gradient descent or other advanced optimization algorithms e.g. fmincg to get the mininum cost-point.

7. In my eyes, decrease the value of 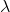 may weaken the effect of regularization, which will improve the accuracy of training set detection and is harmful to the prediction of new data.

The Results:

• nnCostFunction.m

function [J grad] = nnCostFunction(nn_params, ...
                                   input_layer_size, ...
                                   hidden_layer_size, ...
                                   num_labels, ...
                                   X, y, lambda)
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
                 hidden_layer_size, (input_layer_size + 1));

Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
                 num_labels, (hidden_layer_size + 1));

% Setup some useful variables
m = size(X, 1);
         
% You need to return the following variables correctly 
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));

X = [ones(m, 1), X]; 					% 5000*401
a2 = sigmoid(X * Theta1');				% 5000*25
a2 = [ones(size(a2,1),1), a2];			% 5000*26
h = sigmoid(a2 * Theta2'); 				% 5000*10

%for i=1:num_labels
%	pos = log(h(:, i));					% 5000*1
%	neg = log(1-h(:, i));				% 5000*1
%	y_temp = y==i;
%	J = J + (-1 / m) * (y_temp' * pos + (1 - y_temp)' * neg);
%end

for i=1:m
	pos = log(h(i, :));					%1*10
	neg = log(1-(h(i, :)));				%1*10
	y_temp = zeros(num_labels, 1);		%10*1
	y_temp(y(i,1), 1) = 1;				%10*1
	J = J + (pos * y_temp + neg * (1 - y_temp));
end
J =  (-1 / m) * J;
% -------------------------------------------------------------
y_temp = [];
for i=1:num_labels
	y_temp = [y_temp, y==i];										% 5000*10
end
for i=1:m
	delta3 = (h(i, :) - y_temp(i, :))';								% 10*1
	delta2 = Theta2' * delta3 .* a2(i, :)' .* (1- a2(i, :))'; 		% 26*1
	Theta2_grad = Theta2_grad + delta3 * a2(i, :);					% 10*26
	Theta1_grad = Theta1_grad + delta2(2:end, 1) * X(i, :);			% 25*401
end
Theta2_grad = Theta2_grad / m;										% 10*26
Theta1_grad = Theta1_grad / m;										% 25*401
% =========================================================================
sum1 = sum(sum(Theta1(:,2:end) .^ 2));
sum2 = sum(sum(Theta2(:,2:end) .^ 2));
J = J + (lambda / (2 * m)) * (sum1 + sum2);
Theta2_grad = Theta2_grad + lambda / m * [zeros(size(Theta2,1),1), Theta2(:, 2:end)];		% 10*26
Theta1_grad = Theta1_grad + lambda / m * [zeros(size(Theta1,1),1), Theta1(:, 2:end)];		% 25*401

% Unroll gradients
grad = [Theta1_grad(:) ; Theta2_grad(:)];
end

• sigmoidGradient.m

function g = sigmoidGradient(z)

g = zeros(size(z));

g = sigmoid(z) .* (1 - sigmoid(z));

end