匿名属性基代理重加密

云计算中用于访问控制的匿名属性基代理重加密

摘要

作为一种公钥密码原语，基于属性的加密（ABE）在实现云计算中的细粒度访问控制方面具有广阔前景。然而，在ABE投入实际应用之前，必须解决两个具有挑战性的问题，即用户属性隐私保护和访问策略更新。本文首次通过形式化匿名密文策略属性基代理重加密（匿名CP‐ABPRE）的概念并给出具体构造来应对上述挑战。我们提出了一种称为匹配后重加密的新技术，在重加密阶段之前额外引入了一个匹配阶段。该技术利用代理重加密密钥和密文的特殊组件，匿名地检查代理是否能够执行代理重加密。理论分析和仿真结果表明，我们的匿名 CP‐ABPRE方案是安全高效的。版权所有 © 2016 John Wiley & Sons, Ltd。

关键词
云计算；访问控制；基于属性的代理重加密；匿名性；访问策略更新

1. 引言

随着云计算技术的出现，用户的数据在云计算平台上应得到妥善控制和保护。然而，传统的访问控制机制并不适用于云计算。一方面，在传统方案中，服务提供商被数据拥有者完全信任，访问策略由服务提供商定义并执行；另一方面，云用户通常希望与他们指定的用户共享数据，并自行制定访问策略。

作为一种公钥密码学原语，基于属性的加密（ABE）在实现基于云的访问控制系统[1–3]方面具有广阔前景，用户可在其中享有不同且灵活的访问权限。

ABE方案有两种类型，即密钥策略ABE（KP‐ABE）构造和密文策略ABE（CP‐ABE）方案[2]。本文关注后者。

特别是，在CP‐ABE系统中，数据所有者对明文消息 M进行加密，通过实施与属性全集相对应的访问策略，用户只有在其属性满足指定访问策略的情况下才能解密给定的密文。此外，CP‐ABE 不再依赖云存储服务器来抵御某些未授权用户的合谋攻击。CP‐ABE 的上述特性非常适用于在不可信存储上实现细粒度访问控制。另一方面，在军事环境和商业领域中，有必要保护访问策略，因为访问策略本身可能包含敏感信息。同时，访问权限委托在许多实际应用场景中也是不可或缺的。然而，典型的 CP‐ABE 技术无法实现对用户属性隐私的保护或访问策略的更新。

为应对上述挑战，已对匿名ABE进行了研究[4–11]。特别是，文献[11]中引入了一种称为匹配后解密的新技术，以提高解密效率。尽管匿名CP‐ABE能够隐藏访问策略，但其无法支持访问策略更新。另一方面，密文策略基于属性的代理重加密（CP‐ABPRE）[12,13]成功支持访问策略更新，从而允许用户在云计算环境中委托访问权限。然而，CP‐ABPRE无法保护用户属性隐私。据作者所知，目前似乎尚无可用的匿名 CP‐ABPRE方案能够同时保护用户属性隐私并支持访问策略更新。

1.1. 我们的贡献

本研究的贡献可总结如下：
（1）为了在云计算中实现支持访问策略更新的隐私保护访问控制，我们形式化了匿名CP‐ABPRE的概念及其安全模型，并提出了首个匿名CP‐ABPRE方案。需要注意的是，匿名CP‐ABPRE无法通过现有技术（如CP‐ABE和代理重加密（PRE））的简单组合来实现。主要原因是，用户属性隐私保护要求访问策略不在密文中泄露，这导致代理重加密中的属性匹配检测无法实现，从而无法完成访问策略更新。

（2）一种称为匹配后重加密的新型技术被引入到匿名密文策略基于属性的代理重加密中，在代理重加密阶段之前增加了匹配阶段。该技术通过在代理重加密密钥和密文中计算特殊组件，用于检查代理是否能够执行代理重加密。此外，采用匹配后解密技术以提高解密效率。它能够高效地确定属性私钥是否与隐藏的访问策略匹配，而无需进行解密。在所提出的具体构造中，匹配后重加密和匹配后解密这两种新技术能够同时保护用户属性隐私并支持访问策略更新。

(3) 在标准模型中，所提出的匿名CP‐ABPRE方案被证明是安全的。即使是合法的解密者也无法获取密文中的潜在访问策略的任何信息，而只能知道其能够恢复相应的明文。分析和仿真结果表明，该方案是实用的。

1.2. 相关工作

我们总结了典型ABE、匿名ABE以及基于属性的PRE领域的相关工作。

典型ABE

自从属性基加密 [1]被引入以实现访问控制系统以来，已出现了大量关于属性基加密构造 [2,3,14–18]的研究。KP‐ABE和CP‐ABE作为属性基加密的两种变体，由Goyal 等 [2]提出。在KP‐ABE系统中，用户可以从可信属性权威处获取一个与访问策略相对应的私钥。每个密文都与某些属性相关联，而访问策略用于判断某个私钥是否能够解密该密文。在CP‐ABE中，属性权威向用户提供与描述性属性集合相关联的私钥，而密文则对应一个访问策略。首个KP‐ABE方案由[2]构造，其访问策略是单调的。为了提高表达能力，Ostrovsky 等 [14]首次提出了一种支持非单调公式的KP‐ABE系统。然而，相较于KP‐ABE，CP‐ABE更适用于安全的基于云的数据共享环境，因为它赋予了数据拥有者制定策略的能力[19]。首个CP‐ABE方案由 Bethencourt 等 [3]构造，但其存在安全性缺陷，因为其安全性证明仅在通用群模型中成立。为了增强 CP‐ABE的安全性，Cheung 等 [15]构造了一个采用与门策略的CP‐ABE方案，并在标准模型中证明了其安全性。随后，Goyal 等 [16]提出了一个新的 CP‐ABE方案，该方案在标准模型中具备良好的表达能力和安全性。然而，由于效率较低，该方案缺乏实用性。最近，Hohenberger 等 [17]提出了一个具有快速解密特性的属性基加密构造。Garg 等 [18]首次基于多线性映射提出了面向通用电路的属性基加密构造，该构造同时实现了KP‐ABE和CP‐ABE两种形式。Zhang 等[20]提出了一种计算开销小且生成固定大小密文的CP‐ABE方案，该方案能高效支持包含多个属性值和通配符的与门访问策略。尽管上述CP‐ABE方案具有多种吸引人的特性，但仍存在一个弱点：访问策略必须随密文显式传输，因为接收者需要知道如何组合私钥组件以实现成功解密。

匿名ABE

为了保护用户属性隐私，匿名ABE已被研究 [4–11]。在匿名CP‐ABE中，解密者从属性权威处获取其属性私钥。如果私钥不匹配密文所指定的访问策略，则解密者无法恢复明文数据。特别是，他无法猜测该密文指定了何种访问策略。Kapadia 等 [4]构造了一种CP‐ABE方案，可实现对属性正负值的 AND门密文策略隐藏，但无法抵抗合谋攻击。基于隐向量加密原语，Boneh 等 [5]提出了一种谓词加密方案，可通过具有相反语义的谓词来构造匿名CP‐ABE方案。此外，Katz 等 [6]提出了一种内积加密方案，可实现隐藏的CP‐ABE变体。随后，更高效的匿名 CP‐ABE方案被构造出来 [7]。Li 等 [8]提出了一种用于实现可追溯性的匿名CP‐ABE系统。为实现完全安全性，Lai 等 [9,10]提出了基于合数阶群的新假设，提出了两种匿名的CP‐ABE方案。然而，在这些匿名CP‐ABE方案中，用户必须进行解密并判断其属性列表是否与隐藏的访问策略匹配。此类测试需要重复执行，直到成功解密或所有可能的测试均已尝试完毕。因此，这种直接解密方法将面临严重的效率缺陷。为解决该问题，Zhang et al. [11] 构造了一种新的匿名CP‐ABE方案，引入了一种称为匹配后解密的新技术，显著提高了解密效率。需要注意的是，尽管上述匿名CP‐ABE方案保护了用户属性隐私，但未能支持访问策略更新。

基于属性的代理重加密（ABPRE）

在实用的访问控制系统中，CP‐ABPRE 可用于实现访问权限委托，因为它支持访问策略更新。在 CP‐ABPRE 中，代理由用户预先指定。代理可以接收一个代理重加密密钥，该密钥用于将与某个访问策略相关联的密文转换为具有新策略的另一个密文。Blaze et al. [21]首次提出了代理重加密的概念。此后，许多研究工作致力于具有优良特性的代理重加密方案 [22–25]。然而，传统的代理重加密方案并不适用于基于云的环境。在基于云的数据共享中，Liang et al. [12]提出了一种 CP‐ABPRE 方案以实现访问权限委托，该方案被证明是选择性密文策略和选择明文安全的。随后，Luo et al. [13]提出了一种新的 CP‐ABPRE 方案。Kawai et al. [26]提出了一个匿名内积代理重加密方案和一个密文策略函数型代理重加密方案。然而，这两个方案都采用了一次性强不可伪造签名，且后者未能在密文中隐藏密文策略。最近，Liu etal. [27,28]通过在访问策略中引入时间因素，提出了基于时间的ABPRE概念。尽管现有的 CP‐ABPRE 方案支持访问策略更新，但无法保护用户属性隐私。

1.3. 组织结构

本文的其余部分组织如下。在第2节中，我们回顾了一些预备知识，主要包括密码学背景。在第3节中，我们展示了系统模型和设计目标。在第4节中，我们给出了形式化的安全模型。在第5节中，我们描述了匿名 CP‐ABPRE的构造及其安全结果和性能比较。最后，在第6节中得出结论。

2. 预备知识

我们回顾了一些密码学背景知识，然后详细介绍了访问策略。

2.1. 密码学背景

2.1.1. 双线性对

假设G和GT是两个具有某个大素数阶p的循环乘法群，我们分别用1G和1GT表示G和GT的单位元。设 g ∈R G为一个生成元。如果映射e: G × G → GT满足以下性质，则称其为双线性配对：
(1) 双线性的：对于任意 a,b ∈ Zp，e(g^a,g^b) = e(g,g)^{ab}。
(2) 非退化的：存在某些 g1,g2 ∈ G，使得 e(g1,g2) ≠ 1。
(3) 可计算的：对于所有 g1,g2 ∈ G，e(g1,g2) 可以高效地计算。

2.1.2. 复杂性假设

判定性双线性的Diffie–Hellman (DBDH) 假设 ：设 a,b,c,z ∈R Zp，且 g ∈R G 为生成元。若不存在概率多项式时间（PPT）算法能够以不可忽略的优势区分元组 [g, g^a, g^b, g^c, e(g,g)^{abc}] 与 [g, g^a, g^b, g^c, g^z]，则称 DBDH假设 在群 G 中成立。

判定线性（D‐Linear）假设 ：设 g ∈R G 是一个生成元，且 a1,a2,a3,a4,z ∈R Zp。如果不存在概率多项式时间（PPT）算法能够以不可忽略的优势区分元组 [g, g^{a1}, g^{a2}, g^{a1a3}, g^{a2a4}, g^{a3+a4}] 与 [g, g^{a1}, g^{a2}, g^{a1a3}, g^{a2a4}, g^z]，则称 D‐线性假设 在 G 中成立。

计算双线性Diffie‐Hellman（CBDH）假设 ：假设 g ∈R G 是一个生成元，且 a,b,c ∈R Zp。我们说CBDH假设在G中成立，如果给定[g, g^a, g^b, g^c]，没有任何PPT算法能够以不可忽略的优势计算e(g,g)^{abc}。

2.2. 访问策略

在CP‐ABE中，访问策略是一种密文策略。直观上，访问策略是作用于描述性属性的规则W，给定一个属性列表 L时，其返回值为“真”或“假”。仅当W在L上返回 “真”时，L才满足W。通常使用符号L ⊨ W表示L满足 W，而L ⊭ W表示L不匹配W。在我们的构造中，我们考虑由支持带通配符的多值属性的与门组成的访问策略。

作为[15]的一种推广，我们构造中的访问策略与[7]中的相同。对于给定的访问策略W = [W1, W2, …, Wn] 和属性列表L = [L1, L2, …, Ln]，如果对所有 1 ≤ i ≤ n均有Li = Wi 或方程Wi = *成立，则称L满足W（即L ⊨ W），否则 L ⊭ W。注意，访问策略中的通配符*起到与“无关值”（don’t care）相同的作用。

3. 系统模型和设计目标

我们首先在本节中介绍系统模型，然后描述我们的设计目标。

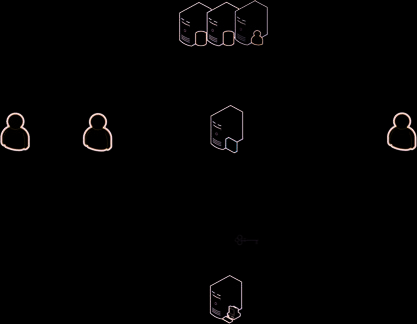
3.1. 系统模型

如图1所示，支持访问策略更新的云计算中匿名属性基访问控制的系统模型包含六个实体：属性权威(AA)、云服务提供商(CSP)、数据拥有者(DO)、原始用户：原始密文的解密者(OU)、代理服务器(PS)和被委托用户：重加密密文的解密者(DU)。由于AA和CSP与典型ABE中的相同，本文仅描述DO、OU、PS和DU这四个实体。

• DO 是拥有数据 M 并希望将其安全地存储在由 CSP 提供的云存储服务器上以进行共享的实体。DO 负责制定基于属性的访问策略 W，使得属性列表 L 满足 L ⊨ W，并通过在 W 下对 M 进行加密，匿名地实施该策略，从而得到原始密文 CT_W。在匿名属性基访问控制中，为了保护用户属性隐私，W 不能在 CT_W 中被泄露。

• 原始用户OU 是一个拥有属性列表L并希望访问存储在云服务提供商CSP上的加密数据CT_W的实体。如果L ⊨ W，其中W是数据拥有者DO指定并隐藏在 CT_W中的底层访问策略，则原始用户OU将成功解密 CT_W。为了提高基于属性的匿名访问控制中解密的效率，采用了一种称为“匹配后解密”的新技术，该技术在解密阶段之前额外引入了一个匹配阶段。具体而言，原始用户OU从云服务提供商CSP下载 CT_W后，应在完全解密之前先检查其属性私钥是否与W匹配。只有当属性匹配成功时，原始用户OU 才执行完全解密。

• PS 是由OU预先指定的实体。PS可以从OU获取代理重加密密钥 R_{K_L→W’}，并通过重加密CT_W生成 CT_{W’}，以实现访问策略从W到W’的更新。为了实现代理重加密，引入了一种称为匹配后重加密的新技术，该技术在重加密阶段之前额外引入了一个匹配阶段。具体而言，在对来自CSP的CT_W进行重加密之前，PS应先确定 R_{K_L→W’} 是否能够重加密CT_W。换句话说，只有当属性匹配成功时，PS才会执行完整的代理重加密操作。

• DU 是希望访问存储在CSP中的重加密数据CT_{W’}的实体。如果DU拥有的属性列表与OU指定的、隐藏在CT_{W’}中的新访问策略W’相匹配，则他将成功解密CT_{W’}。类似地，DU可采用匹配后解密技术来提高解密效率。

3.2. 设计目标

• 数据机密性 。如果用户属性列表与对应密文指定的访问策略不匹配，数据拥有者将尽力防止未授权用户访问明文。此外，云服务提供商和代理服务器不得访问加密数据的明文。

• 抗共谋 。某些用户可能会结合他们的属性私钥来解密任何单独用户都无法解密的密文。在实际应用中，访问控制系统，抗共谋的属性意味着这些共谋者无法恢复明文。

• 属性隐私保护 。在支持访问策略更新的基于属性的访问控制中，访问策略可能是敏感的，需要加以保护。一方面，代理服务器应在不知道访问策略的情况下完成代理重加密；另一方面，即使用户的属性列表与密文策略匹配，该用户也不应获知数据拥有者指定的访问策略中的任何信息，除了其能够访问相应明文这一事实之外。

• 主密钥安全 。即使代理服务器与数据用户共谋，他们也无法获取原始用户的原始解密密钥。

此外，还应考虑性能相关问题。在匿名CP‐ABPRE中，应在完整的代理重加密和解密之前进行高效的属性匹配检测。

4. 形式化安全模型

在给出形式化安全模型之前，我们首先阐述匿名 CP‐ABPRE的定义。一个匿名CP‐ABPRE方案由以下六个算法组成：

• Setup(1^λ) → (PK, MK) ：该算法由AA运行。以安全参数 λ作为输入，输出系统公钥PK和主密钥MK。注意，PK为所有用户所知，而SK需保密。

• KeyGen(PK, MK, L) → SK_L ：该密钥生成算法由 AA运行。输入为PK、MK以及属性列表L，输出与 L相关的属性私钥SK_L。

• Encrypt(PK, M, W) → CT_W ：该加密算法由DO运行。DO指定一个访问策略W。输入为PK、消息M和W，生成密文CT_W作为 M关于W的加密结果。为了实现访问策略的匿名性，W不能在CT_W中被暴露。

• RKGen(PK, SK_L, W’) → R_{K_L→W’} ：该算法由OU或DU运行以获取代理重加密密钥。输入为PK、与L相关的属性私钥SK_L以及访问策略W’，输出R_{K_L→W’}作为代理重加密密钥。

• Reencrypt(PK, R_{K_L→W’}, CT_W) → CT_{W’}或? ：该代理重加密算法由PS运行。其包含两个阶段，即属性匹配检测和重加密阶段。输入为PK、R_{K_L→W’}和密文CT_W，PS在不知道W的情况下执行以下操作：
  1. 匹配阶段 ：如果L ⊭ W，则以极大概率返回？以终止重新加密。否则，通过启动重加密阶段结束匹配阶段。
  2. 重加密阶段 ：它生成一个对应于 W′ 的代理重加密密文 CT_{W′}，其中明文与 CT_W 中的明文相同。

• Decrypt(PK, CT_W, SK_L) → M或? ：解密算法由原始用户 OU或数据用户DU运行。该过程包含两个阶段，即属性匹配检测和解密阶段。输入为公钥PK、在访问策略 W下关于明文消息M的密文CT_W，以及与属性集L相关的私钥SK_L，拥有私钥SK_L的用户（OU或DU）可在不知道访问策略W的情况下对密文CT_W进行测试并解密，具体步骤如下：
  1. 匹配阶段 ：如果L ⊭ W，则以压倒性概率返回？以终止解密。否则，匹配阶段通过启动解密阶段结束。
  2. 解密阶段 ：它返回M。

随后，为了实现第3.2节中的安全目标，我们对攻击者的能力进行建模，并定义相应的安全概念。数据机密性、抗共谋和属性隐私保护的设计目标体现在选择性密文策略和选择明文攻击下的不可区分性 (IND‐sCP‐CPA) [2,3,15]模型中。主密钥安全目标则体现在选择性主密钥安全(sMKS)模型中。这两个模型均为攻击者与挑战者之间的交互式游戏。

4.1 IND‐sCP‐CPA游戏

初始化 ：A向挑战者提交两个挑战密文策略 W*0 和W*1。

设置 ：挑战者指定一个较大的安全参数 λ，并运行Setup算法以生成主密钥SK和相应的公钥PK。挑战者将SK保密，并将PK公开。

阶段1 ：攻击者A以多项式时间查询以下预言机：
- 密钥生成预言机 OKeyGen ：A提交一个属性列表L，若满足（L ⊭ W*0 ∧ L ⊭ W*1）或（L ⊨ W*0 ∧ L ⊨ W*1），则挑战者将SK_L返回给 A；否则输出?。
- 重加密密钥生成预言机 ORKGen ：攻击者 A提交L和W，若满足（L ⊭ W*0 ∧ L ⊭ W*1）或（L ⊨ W*0 ∧ L ⊨ W*1），则挑战者返回 A 重加密密钥R_{K_L→W}；否则输出?。
- 重加密预言机 OReEnc ：A提交L、W0以及一个在访问策略 W下的匿名密文CT_W，若满足（(L ⊭ W*0 ∧ L ⊭ W*1) 或 (L ⊨ W*0 ∧ L ⊨ W*1)）且L ⊨ W，则挑战者返回 ACT_{W0}；否则输出?。

挑战 ：在阶段1结束后，A输出两个等长的消息 M0和M1。要求如果任何满足L0=L1的私钥在L上且满足L ⊨ W*0 ∧ L ⊨ W*1已被查询，则M0=M1。挑战者随机选择一个比特 β ∈ {0, 1}，计算CT_{Wβ} = Encrypt(PK, M_β, W* β)，并将CT {Wβ} 发送给 A，其中W*_β是隐藏的。

第二阶段 ：它与阶段1类似。

猜测 ：A输出一个比特 β’ ∈ {0, 1} 作为对 β 的猜测，如果 β’ = β，则攻击者A赢得上述游戏。

在IND‐sCP‐CPA游戏中，我们定义A的优势为
Adv_{CP-ABPRE}^{IND-sCP-CPA}(A) = |Pr[β’= β] – 1/2|。

备注 1 . 在该模型中，挑战阶段要求 M0= M1，如果攻击者获得了同时匹配 W*0 和 W*1 的私钥 SK_L。否则，攻击者可以直接解密挑战密文以获得比特值 β。因此，显然可知，若无此类限制，匿名CP‐ABPRE的安全模型将毫无意义。

4.2. sMKS 游戏

初始化 ：A向挑战者提交属性列表L*。

设置 ：与 IND‐sCP‐CPA 游戏中的设置相同。

查询 ：A在多项式时间内查询以下预言机：
- 密钥生成预言机 OKeyGen ：A提交一个属性列表L，如果L ≠ L*，挑战者将SK_L返回给 A；否则，输出?。
- 重加密密钥生成预言机 ORKGen ：A提交L和W，挑战者为 A生成一个代理重加密密钥 R_{K_L→W}。
- 重加密预言机 OReEnc ：攻击者 A提交一个属性列表L、访问策略W0以及在访问策略 W下的密文CT_W，挑战者将CT_{W0}作为重加密密文返回给 A。注意，访问策略W不会在CT_W中公开，以实现匿名性。

输出 ：A输出一个属性私钥 SK_{L*}，当且仅当该私钥 SK_{L*}对于 L* 是有效时，输出成功。

在 sMKS 游戏中，我们定义 A 的优势为 Adv_{CP-ABPRE}^{sMKS}(A) = Pr[A成功]。

定义 1 . 如果不存在概率多项式时间攻击者能够以不可忽略的优势攻破上述匿名CP-ABPRE方案的 IND-sCP-CPA（或sMKS）安全游戏，则称该匿名 CP-ABPRE方案是IND-sCP-CPA（或sMKS）安全的。

5. 匿名CP‐ABPRE方案

5.1. 提出的构造

Setup(1^λ) ：选择两个具有大素数阶 p 的循环乘法群 G 和 GT。令 e: G × G → GT 是一个双线性配对。选择 g 作为 G 的生成元，E: G → GT 为 G 与 GT 之间的编码 [12,13]。假设全局属性集为 U={ω₁, ω₂, …, ωₙ}。每个属性具有多个值，第i个属性 ωᵢ 的多值集合记为 Sᵢ = {vᵢ,₁, vᵢ,₂, …, vᵢ,ₙᵢ}。AA 选择 g₂, g₃ ∈R G 和 y ∈R Zₚ。对于每个属性 ωᵢ（其中 1 ≤ i ≤ n），AA 还选择 {Tᵢ,ₜ ∈R G}₁≤ₜ≤ₙᵢ 和 {aᵢ,ₜ, bᵢ,ₜ ∈R Zₚ}₁≤ₜ≤ₙᵢ。然后，AA 计算 g₁ = gʸ, Y = e(g₁, g₂) 以及 {{Aᵢ,ₜ = Tᵢ,ₜ^{aᵢ,ₜ}, Bᵢ,ₜ = Tᵢ,ₜ^{bᵢ,ₜ}}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ。系统公钥为 PK = ⟨g, g₁, g₂, g₃, Y, {{Tᵢ,ₜ, Aᵢ,ₜ, Bᵢ,ₜ}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ⟩，主密钥为 MK = ⟨y, {{aᵢ,ₜ, bᵢ,ₜ}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ⟩。

KeyGen(PK, MK, L) ：在接收到属性列表 L = [L₁, L₂, …, Lₙ] 后，攻击者A选择 r₀, Nd ∈R Zₚ，以及 {rᵢ, řᵢ, δᵢ ∈R Zₚ}₁≤ᵢ≤ₙ，设置 r = Σᵢ₌₁ⁿ rᵢ，ř = Σᵢ₌₁ⁿ řᵢ，并计算 D₀ = g⁻ʳ², D̃₀ = g⁻ř², ND₀ = g³ᴺᵈ, D ₀ = gʳ⁰。对于 i 从 1 到 n，假设索引满足 Lᵢ = vᵢ,ₖᵢ，攻击者A计算 [D ,ᵢ, Dᵢ,₀, Dᵢ,₁, Dᵢ,₂] = [g²^{řᵢ} Tᵢ,ₖᵢ^{r₀}, g²^{rᵢ} Bᵢ,ₖᵢ^{-δᵢ aᵢ,ₖᵢ}, g^{-δᵢ aᵢ,ₖᵢ}, g^{-δᵢ bᵢ,ₖᵢ}]。然后，SK_L = ⟨D₀, D̃₀, ND₀, D ₀, {D ,ᵢ, Dᵢ,₀, Dᵢ,₁, Dᵢ,₂}₁≤ᵢ≤ₙ⟩。

Encrypt(PK, M, W) ：在访问策略 W = [W₁, W₂, …, Wₙ] 下对 M ∈ GT 进行加密，DO 选择 s, s’, s’’ ∈R Zₚ，并计算 QC = M·Yˢ, C₀ = gˢ, CRE = g³ˢ, C = Yˢ’ 和 C₀’ = 1_G。对于 1 ≤ i ≤ n 且 1 ≤ t ≤ nᵢ，DO 计算 [Cᵢ,ₜ, , Cᵢ,ₜ,₁, Cᵢ,ₜ,₂] 为 [Tᵢ,ₜ^{s’}, Bᵢ,ₜ^{s-s’‘}, Aᵢ,ₜ^{s’‘}] 如果 vᵢ,ₜ ∈ Wᵢ。否则，[Cᵢ,ₜ, , Cᵢ,ₜ,₁, Cᵢ,ₜ,₂] 是 G 中的随机元素。最终，关于 W 的 M 的密文为 CT_W = ⟨C , C₀’, QC, C₀, CRE, {{Cᵢ,ₜ,*, Cᵢ,ₜ,₁, Cᵢ,ₜ,₂}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ⟩。

RKGen(PK, SK_L, W’) : 设 SK_L = ⟨D₀, D̃₀, ND₀, D ₀, {D ,ᵢ, Dᵢ,₀, Dᵢ,₁, Dᵢ,₂}₁≤ᵢ≤ₙ⟩ 且 W’ 为一个访问策略。为了获得与 W’ 相关联的代理重加密密钥，它选择 d ∈R Zₚ 并计算 gᵈ, D̃₀’ = D̃₀·(ND₀)ⁿ, ND₀’ = ND₀·g³ᵈ, D ‘ᵢ = D ,ᵢ·g³ᵈ, D’ᵢ,₀ = Dᵢ,₀·g³ᵈ。同时，它设置 D’₀ = D₀, D ‘₀ = D ₀, D’ᵢ,₁ = Dᵢ,₁, D’ᵢ,₂ = Dᵢ,₂，并计算 C = Encrypt(PK, E(gᵈ), W’)。然后，R_{K_L→W’} = ⟨L, D’₀, D̃’₀, ND’₀, D ‘₀, {D ‘ᵢ, D’ᵢ,₀, D’ᵢ,₁, D’ᵢ,₂}₁≤ᵢ≤ₙ, C⟩ 是对应于 W’ 的代理重加密密钥。

Reencrypt(PK, R_{K_L→W’}, CT_W) ：在接收到针对访问策略 W’ 的 R_{K_L→W’} 以及在访问策略 W 下的 CT_W 后，代理服务器在不知道访问策略 W 的情况下执行以下操作：
1. 匹配阶段 ：代理服务器计算 C ’ = e(C₀’, ND’₀ⁿ)，并检查以下等式(1)是否成立。具体而言，当且仅当等式(1)成立时，L ⊨ W。
$$
C \cdot C ’ = \frac{e(C₀, D̃’₀) \prod_{i=1}^n e(D ‘ᵢ, Cᵢ,ₖᵢ, )}{e(\prod_{i=1}^n Cᵢ,ₖᵢ, , D ‘₀)}
$$
其中假设索引满足 Lᵢ = vᵢ,ₖᵢ。如果 L ⊭ W，则返回？。否则，启动重加密阶段。
2. 重加密阶段 *：对于 1 ≤ i ≤ n，假设索引满足 Lᵢ = vᵢ,ₜ，代理服务器 PS 计算
$$
Eᵢ = \frac{e(C₀, D’ᵢ,₀)}{e(Cᵢ,ₜ,₁, D’ᵢ,₁) \cdot e(Cᵢ,ₜ,₂, D’ᵢ,₂)} = e(g, g₂)^{s rᵢ} \cdot e(g, g₃)^{s d}
$$
随后，它计算
$$
C = e(C₀, D’₀) \cdot \prod_{i=1}^n Eᵢ = e(g, g₂)^{y s} \cdot e(g, g₃)^{n s d}
$$
并输出一个代理重加密密文 CT_{W’} = ⟨QC, CRE, C, C⟩。根据后续的解密算法可知，数据用户 DU 仅需 gᵈ 即可解密该代理重加密密文。因此，我们可以得到一个两次代理重加密密文 CT_{W’‘} = ⟨QC, CRE, C, C’⟩，其中 C’ 是基于算法 Reencrypt，以密文 C 和另一个代理重加密密钥 R_{K_{L’}→W’‘} 作为输入生成的。具体而言，C’ = Reencrypt(PK, R_{K_{L’}→W’‘}, C)。类似地，可生成多次代理重加密密文。

Decrypt(PK, CT_W, SK_L) ：具有私钥 SK_L 的用户对密文 CT_W 进行测试并解密，过程如下：
- 如果 CT_W 是原始密文，用户执行以下操作：
1. 匹配阶段 ：用户根据以下等式(2)检查是否满足 L ⊨ W。假设索引满足 Lᵢ = vᵢ,ₖᵢ，当且仅当等式(2)成立时，L ⊨ W 成立
$$
C = \frac{e(C₀’, D̃₀) \prod_{i=1}^n e(D ,ᵢ, Cᵢ,ₖᵢ, )}{e(\prod_{i=1}^n Cᵢ,ₖᵢ, , D ,₀)}
$$
如果 L ⊭ W，则返回？。否则，它将启动解密阶段。
2. 解密阶段 ：假设索引满足 Lᵢ = vᵢ,ₖᵢ，用户计算
$$
M = \frac{QC}{\prod_{i=1}^n e(Cᵢ,ₖᵢ,₁, Dᵢ,₁) \cdot e(Cᵢ,ₖᵢ,₂, Dᵢ,₂) \cdot e(C₀, D₀) \cdot \prod_{i=1}^n e(C₀, Dᵢ,₀)}
$$
- 否则，如果 CT_W 是一个一次性代理重加密密文，由 ⟨QC, CRE, C, C⟩ 组成，则用户执行以下操作：
1. 匹配阶段 ：用户根据等式(2)中的方法，检查 L ⊨ W 是否符合 C。如果 L ⊭ W，算法返回？；否则，进入解密阶段。
2. 解密阶段 *：
– 执行对 E(gᵈ) 的原始密文 C 使用私钥 SK_L 的解密，并将其解码为 gᵈ。
– 计算
$$
\frac{QC}{e(CRE, gᵈ)ⁿ / C} = M
$$
- 否则，如果 CT_W 是一个多时态代理重加密密文，则解密过程类似于前述阶段。假设 CT_W 是一个 N+1 次代理重加密密文，由 ⟨QC, CRE, C, C’⟩ 组成，其中 C’ 是 N 次对 E(gᵈ) 的代理重加密密文，则用户执行以下操作：
– 执行对 N 次代理重加密密文 C’ 的解密。如果算法不返回？，用户恢复 E(gᵈ)，解码为 gᵈ 并继续。
– 计算
$$
\frac{QC}{e(CRE, gᵈ)ⁿ / C} = M
$$

5.2. 安全性结果

定理1 . 该匿名CP-ABPRE方案在DBDH假设和D-线性假设下，于IND-sCP-CPA模型中是安全的，且无需随机预言。因此，该方案实现了数据机密性、抗共谋和属性隐私保护的安全目标。

证明 。我们证明所提出的匿名CP‐ABPRE方案在标准模型下基于DBDH和D‐线性假设是IND‐sCP‐CPA安全的。具体而言，如果存在一个多项式时间攻击者A，能够在IND‐sCP‐CPA模型下以优势 ε_IND 攻击该方案，则可得 ε_IND 是可忽略的，且 ε_IND ≤ ε_DBHD + nε_DL，其中 ε_DBHD 和 ε_DL 分别表示DBDH挑战和D‐线性挑战的区分器的优势，n是系统的属性集合的大小。

假设A在游戏开始时提交了挑战密文策略 W _0 = [W _0,₁, W _0,₂, …, W _0,ₙ] 和 W _1 = [W _1,₁, W _1,₂, …, W _1,ₙ]。基于IND‐sCP‐CPA安全模型，为了证明 A在原始安全游戏G中无法获得不可忽略的优势，采用了一系列混合游戏。首先，将G略微修改为另一个游戏 G₀。游戏G和G₀的定义相同，仅在挑战密文的生成上有所不同。具体而言，在G₀中，如果攻击者未获得与满足条件[L ⊨ W _0 ∧ L ⊨ W _1]的属性列表L相关的属性私钥SK_L，则无论何种情况，挑战密文分量 C 均为GT中的随机元素，而其他挑战密文组件以正常方式生成。另一方面，如果A获得了满足[L ⊨ W _0 ∧ L ⊨ W _1]的私钥 SK_L，则所有密文组件均被正确生成。在这种情况下，我们有G = G₀。随后，我们通过修改密文组件 {{Cᵢ,ₜ,*, Cᵢ,ₜ,₁, Cᵢ,ₜ,₂}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ 来调整游戏G₀，并依次定义以下游戏。

如果 vᵢ,ₜ 满足 (vᵢ,ₜ ∉ W _0,ᵢ ∧ vᵢ,ₜ ∉ W _1,ᵢ) 或 (vᵢ,ₜ ∈ W _0,ᵢ ∧ vᵢ,ₜ ∈ W _1,ᵢ)，则在所有游戏中，{Cᵢ,ₜ, , Cᵢ,ₜ,₁, Cᵢ,ₜ,₂} 的生成方式与真实游戏相同。当存在 vᵢ,ₜ 满足 (vᵢ,ₜ ∉ W _0,ᵢ ∧ vᵢ,ₜ ∈ W _1,ᵢ) 或 (vᵢ,ₜ ∈ W _0,ᵢ ∧ vᵢ,ₜ ∉ W _1,ᵢ) 时，在新的修改游戏 G_l 中，无论随机硬币如何，均将来自G的随机元素赋给 {Cᵢ,ₜ, , Cᵢ,ₜ,₁, Cᵢ,ₜ,₂}，尽管它们在 G_{l–1} 中是正常生成的。该过程重复进行，直到不存在满足 (vᵢ,ₜ ∉ W _0,ᵢ ∧ vᵢ,ₜ ∈ W _1,ᵢ) 或 (vᵢ,ₜ ∈ W _0,ᵢ ∧ vᵢ,ₜ ∉ W _1,ᵢ) 的组件 vᵢ,ₜ 为止。在最后一个游戏中，A的优势为零，因为挑战密文与随机硬币无关。根据上述方法，我们将 G_{l–1} 中的良构组件在 G_l 中替换为来自G的随机元素，从而将D‐线性挑战嵌入到密文中，并且可以借助 G_{l–1} 和 G_l 的区分器来生成对D‐线性挑战的区分器。

假设上述游戏依次构成 {G, G₀, G₁, …, G_{l_max}}，其中 G 是原始攻击游戏，G_{l_max} 是最后一个游戏。令 E 表示在原始游戏 G 中发生 β’= β 的事件，E_l 表示在 G_l 中发生 β’= β 的事件，其中 0 ≤ l ≤ l_max。那么，ε_IND = |Pr[E] – 1/2| = |Pr[E] – Pr[E_{l_max}]|。根据三角不等式可得
$$
ε_IND ≤ |Pr[E] – Pr[E₀]| + \sum_{l=1}^{l_max} |Pr[E_{l–1}] – Pr[E_l]|
$$
下文中，我们分别通过证明引理2和引理3得出： |Pr[E]– Pr[E₀]| ≤ ε_DBHD 以及 |Pr[E_{l–1}]– Pr[E_l]| ≤ ε_DL 对于 1 ≤ l ≤ l_max 成立。因此显然 ε_IND ≤ ε_DBHD + nε_DL 是可忽略的，从而在DBDH和D‐线性假设下，所提出的匿名CP‐ABPRE构造是 IND‐sCP‐CPA安全的。

引理2 。在DBDH假设下，攻击者A在G中的优势与在G₀中的优势之差在 |Pr[E] – Pr[E₀]| ≤ ε_DBHD 中是可忽略的。

证明 。假设 A在G和G₀中的优势之间存在差值 ε₀。我们将构建一个模拟器 S₀，使得其以优势ε₀参与DBDH游戏。假设DBDH挑战者给出挑战 [g, gᵃ, gᵇ, gᶜ, Z]，其中分量 Z以相等概率为 e(g,g)ᵃᵇᶜ 或群GT中的一个随机元素，模拟过程如下：

初始化 ：S₀运行 A并从 A接收两个挑战密文策略 W _0 = [W _0,₁, W _0,₂, …, W _0,ₙ] 和 W _1 = [W _1,₁, W _1,₂, …, W _1,ₙ]。然后 S₀抛掷一枚随机硬币 β ∈ {0,1}。为了向 A生成公钥PK，模拟器 S₀计算 g₁ = gᵃ、g₂ = gᵇ，并设置 Y = e(g₁,g₂) = e(g,g)ᵃᵇ，这意味着 y = a。此外，S₀选择 μ ∈R Zₚ 并计算 g₃ = g^μ。对于 1 ≤ i ≤ n，选择 {ηᵢ,ₜ, aᵢ,ₜ, bᵢ,ₜ ∈R Zₚ}₁≤ₜ≤ₙᵢ，并生成 {Tᵢ,ₜ, Aᵢ,ₜ, Bᵢ,ₜ}₁≤ₜ≤ₙᵢ 如下：
- 如果 vᵢ,ₜ ∈ W _β,ᵢ，则 S₀ 设置 Tᵢ,ₜ = g^{ηᵢ,ₜ}，并且 Aᵢ,ₜ = Tᵢ,ₜ^{aᵢ,ₜ}，Bᵢ,ₜ = Tᵢ,ₜ^{bᵢ,ₜ};
- 如果 vᵢ,ₜ ∉ W _β,ᵢ，则 S₀ 设置 Tᵢ,ₜ = g^{ηᵢ,ₜ b}，并且 Aᵢ,ₜ = Tᵢ,ₜ^{aᵢ,ₜ}，Bᵢ,ₜ = Tᵢ,ₜ^{bᵢ,ₜ}。

然后 PK = ⟨g, g₁, g₂, g₃, Y, {{Tᵢ,ₜ, Aᵢ,ₜ, Bᵢ,ₜ}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ⟩ 并 S₀发送公钥 PK。

阶段1 ：以下查询由 A 发起。
- 密钥生成查询 OKeyGen(L) ：假设 A 提交 L = [L₁, L₂, …, Lₙ] 以获取相应的私钥。仅考虑 L ⊭ W _0 ∧ L ⊭ W _1 的情况。原因是根据我们的安全模型定义，当 L ⊨ W _0 ∧ L ⊨ W _1 时，消息 M₀ 等于 M₁。因此，G 与 G₀ 相同，攻击者 A 在 G 和 G₀ 中的优势没有差异。相应地，S₀ 直接中止并进行随机猜测。

在 L ⊭ W _0 ∧ L ⊭ W _1 的情况下，必然存在一个整数 j ∈ {1, 2, …, n}，使得 Lⱼ = vⱼ,ₖⱼ 且 Lⱼ ∉ W*_β,ⱼ。对于 1 ≤ i ≤ n，S₀选择 r’ᵢ, ř’ᵢ ∈ Zₚ，然后设置 rⱼ = a + r’ⱼ, řⱼ = a + ř’ⱼ，并对每个 i ≠ j，设置 rᵢ = r’ᵢ, řᵢ = ř’ᵢ。最后，S₀计算 r = Σᵢ₌₁ⁿ rᵢ = a + Σᵢ₌₁ⁿ r’=ᵢ, ř = Σᵢ₌₁ⁿ řᵢ = a + Σᵢ₌₁ⁿ ř’=ᵢ。分量 [D₀, D̃₀] 可以被计算为
$$
D₀ = \prod_{i=1}^n g^{-r’ i}_2 = g^{-\sum {i=1}^n r’ i}_2 = g^{a-r}_2 = g^{y-r}_2
$$
$$
D̃₀ = \prod {i=1}^n g^{-ř’ i}_2 = g^{-\sum {i=1}^n ř’_i}_2 = g^{a-ř}_2 = g^{y-ř}_2
$$
S₀还选择 d ∈R Zₚ并计算 ND₀ = g³ᵈ。

此外，S₀可以如下计算分量 [D ,ᵢ, Dᵢ,₀, Dᵢ,₁, Dᵢ,₂]：
- 对于 j，S₀计算
$$
D ,ⱼ = g²^{řⱼ} Tⱼ,ₖⱼ^{r₀} = g^{ř’ⱼ+a+r₀ ηⱼ,ₖⱼ}_2 = g^{ř’ⱼ+ζ}_2
$$
$$
Dⱼ,₀ = g²^{rⱼ} Bⱼ,ₖⱼ^{-aⱼ,ₖⱼ} = g^{r’ⱼ+ζ}_2
$$
$$
Dⱼ,₂ = g^{-δⱼ bⱼ,ₖⱼ} = (g^{bⱼ,ₖⱼ})^{-δⱼ}
$$
其中 ζ, η ∈R Zₚ由 S₀ 选择。它设置 r₀ = (ζ–a)/ηⱼ,ₖⱼ 以及 δⱼ = –a/(aⱼ,ₖⱼ bⱼ,ₖⱼ ηⱼ,ₖⱼ)，因此 g^{δⱼ} = g^{a/(aⱼ,ₖⱼ bⱼ,ₖⱼ ηⱼ,ₖⱼ)} g^{-1/(aⱼ,ₖⱼ bⱼ,ₖⱼ ηⱼ,ₖⱼ)}，这在 Dⱼ,₁ 和 Dⱼ,₂ 的计算中使用。
- 此外，S₀设置 D ,₀ = gʳ⁰ = g^{(ζ–a)/ηⱼ,ₖⱼ} = g^{ζ/ηⱼ,ₖⱼ} g^{-1/ηⱼ,ₖⱼ}。
- 对于 i ≠ j 的情况，S₀ 选择 δᵢ ∈ Zₚ 并计算
$$
D ,ᵢ = g²^{řᵢ} Tᵢ,ₖᵢ^{r₀} = g^{ř’ᵢ}_2 (g^{r₀})^{ηᵢ,ₖᵢ}
$$
$$
Dᵢ,₀ = g²^{rᵢ} Bᵢ,ₖᵢ^{-δᵢ} = g^{r’ᵢ}_2 g^{aᵢ,ₖᵢ bᵢ,ₖᵢ δᵢ ηᵢ,ₖᵢ} (g^{bᵢ,ₖᵢ})^{-δᵢ}
$$

最终生成的私钥为 SK_L = ⟨D₀, D̃₀, ND₀, D ,₀, {D ,ᵢ, Dᵢ,₀, Dᵢ,₁, Dᵢ,₂}₁≤ᵢ≤ₙ⟩。

• 重加密密钥生成查询 ORKGen(L, W) ：A提交 L = [L₁, L₂, …, Lₙ] 和一个密文策略 W = [W₁, W₂, …, Wₙ] 作为重加密密钥查询。出于与私钥查询ORKGen(·)相同的原因，我们仅考虑 L ⊭ W _0 ∧ L ⊭ W _1 的情况。在此情况下，S₀向 OKeyGen预言机提交L并获得 SK_L = ⟨D₀, D̃₀, ND₀, D ,₀, {D ,ᵢ, Dᵢ,₀, Dᵢ,₁, Dᵢ,₂}₁≤ᵢ≤ₙ⟩。为了获得对应于W的重加密密钥，S₀选择 d ∈R Zₚ 并计算 gᵈ, D̃’₀ = D̃₀(ND₀)ⁿ, ND’₀ = ND₀g³ᵈ, D ‘ᵢ = D ,ᵢg³ᵈ, D’ᵢ,₀ = Dᵢ,₀g³ᵈ。同时，设置 D’₀ = D₀, D ‘₀ = D ,₀, D’ᵢ,₁ = Dᵢ,₁, D’ᵢ,₂ = Dᵢ,₂，并计算 C 为 E(gᵈ) 关于 W 的相应密文，即 C = Encrypt(PK, E(gᵈ), W)。最后，对应于 W 的重加密密钥 R_{K_L→W} 为 ⟨L, D’₀, D̃’₀, ND’₀, D ‘₀, {D ‘ᵢ, D’ᵢ,₀, D’ᵢ,₁, D’ᵢ,₂}₁≤ᵢ≤ₙ, C⟩。

• Reencrypt query OReEnc(L, W’, CT_W) ：出于与查询 OKeyGen(·) 相同的原因，仅考虑 L ⊭ W _0 ∧ L ⊭ W _1。在这种情况下，S₀将 (L, W’) 提交给重加密密钥查询 ORKGen(·) 并获得重加密密钥 R_{K_L→W’}。然后，S₀根据相应算法继续执行。

挑战 ：攻击者A提交两个挑战消息M₀和M₁。模拟器 S₀设置 QC = M_β Z 且 C₀ = gᶜ，这意味着 s = c，并计算 CRE = g³ˢ = (g³)ˢ = (gᶜ)³。此外，选择 s’, s’’ ∈R Zₚ，{δᵢ ∈R G|1 ≤ i ≤ n}，使得 Πᵢ₌₁ⁿ δᵢ = 1，并设置 C = Yˢ’ 和 C₀’ = gˢ’。然后对于 1 ≤ i ≤ n 且 1 ≤ t ≤ nᵢ，模拟器 S₀根据访问策略 W _β 计算 [Cᵢ,ₜ, , Cᵢ,ₜ,₁, Cᵢ,ₜ,₂] 如下：
- 如果 vᵢ,ₜ ∈ W _β,ᵢ，则 Cᵢ,ₜ, = δᵢ Tᵢ,ₜ^{s’} = δᵢ g^{ηᵢ,ₜ s’}, Cᵢ,ₜ,₁ = Bᵢ,ₜ^{s–s’‘} = Tᵢ,ₜ^{bᵢ,ₜ(s–s’‘)} = g^{ηᵢ,ₜ bᵢ,ₜ(s–s’‘)} 和 Cᵢ,ₜ,₂ = Aᵢ,ₜ^{s’‘} = Tᵢ,ₜ^{aᵢ,ₜ s’‘} = g^{ηᵢ,ₜ aᵢ,ₜ s’‘};
- 如果 vᵢ,ₜ ∉ W _β,ᵢ，则 [Cᵢ,ₜ,*, Cᵢ,ₜ,₁, Cᵢ,ₜ,₂] 是 G 中的随机元素。

显然，S₀正确地生成了关于 W _β 的挑战密文 M_β，即 CT_{W _β} = ⟨C , C₀’, QC, C₀, CRE, {{Cᵢ,ₜ, , Cᵢ,ₜ,₁, Cᵢ,ₜ,₂}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ⟩。

第二阶段 ：模拟器 S₀按照阶段1的步骤进行。

猜测 ：对于 β，攻击者 A输出一个猜测 β’。然后，当 β’= β成立时，S₀输出1，否则输出0。根据我们的假设，在G和G₀中，A正确猜测 β的概率之间存在差值 ε₀。注意，当 Z= e(g, g)ᵃᵇᶜ 时，A处于G中；而当 Z是GT中的随机元素时，A处于G₀中。因此，S₀在DBDH游戏中具有优势 ε₀。根据DBDH假设，ε₀ ≤ ε_DBHD 成立。因此，攻击者A在G与在G₀中的优势之差在 λ 上是可忽略的。具体而言，我们有 |Pr[E]– Pr[E₀]| = ε₀ ≤ ε_DBHD。

引理3 。在D-线性假设下，攻击者A在 G_{l–1} 与 G_l 中的优势之差对于 1 ≤ l ≤ l_max 而言在 λ 中可忽略。具体而言， |Pr[E_{l–1}] – Pr[E_l]| ≤ ε_DL 对于 1 ≤ l ≤ l_max 成立。

证明 。假设攻击者A在 G_{l–1} 和 G_l 中的优势之间存在不可忽略的差异 ε_l。接下来，我们将构建一个模拟器 S_l，其能够在D‐线性游戏中获得优势 ε_l。假设D‐线性挑战者给出一个挑战 [g, g^{z₁}, g^{z₂}, Z, g^{z₂ z₄}, g^{z₃+z₄}]，其中 Z 以相同概率为 g^{z₁ z₃} 或群G中的一个随机元素，S_l 构造如下的模拟。

如定理1所述，在游戏 G_{l–1} 中，密文组件 {C_{i_l,t_l, }, C_{i_l,t_l,1}, C_{i_l,t_l,2}} 与 k_{i_l} = t_l 的计算方式与实际方案中的相同，而在游戏 G_l 中，对于任意随机硬币 β，这些组件为来自群G的随机元素。不失一般性，假设 (v_{i_l,t_l} ∉ W _0,i_l ∧ v_{i_l,t_l} ∈ W*_1,i_l)。模拟过程如下：

Init : S_l 运行 A 并收到来自 A 的两个挑战密文策略 W _0 = [W _0,₁, W _0,₂, …, W _0,ₙ] 和 W _1 = [W _1,₁, W _1,₂, …, W _1,ₙ]。随后，S_l 随机抛硬币 β ∈ {0,1}。如果 β = 0, S_l 直接终止并使用一个随机猜测。原因是，如果 β = 0 其中（v_{i_l,t_l} ∉ W _0,i_l ∧ v_{i_l,t_l} ∈ W _1,i_l），根据游戏的定义，我们有 G_{l–1} = G_l。因此，G_{l–1} 中的挑战密文与 G_l 中的挑战密文相同；因此，A在 G_{l–1} 中的优势与在 G_l 中的优势相同。据此，以下假设 β = 1。

设置 ：为了为A生成公钥PK，模拟器 S_l 设置 g₁ = g^{z₁}，这意味着 y = z₁。然后，S_l 选择 μ₂, μ₃ ∈R Zₚ 并计算 g₂ = g^{μ₂}，g₃ = g^{μ₃} 以及 Y = e(g₁, g₂)。对于每个属性 i（其中 1 ≤ i ≤ n），S_l 选择 {ηᵢ,ₜ ∈R Zₚ}₁≤ₜ≤ₙᵢ，并生成 {Tᵢ,ₜ}₁≤ₜ≤ₙᵢ 如下：如果 vᵢ,ₜ ∈ W*_β,ᵢ，则 Tᵢ,ₜ = g^{ηᵢ,ₜ}；否则，Tᵢ,ₜ = (g^{z₁})^{ηᵢ,ₜ}。此外，对于 1 ≤ i ≤ n，S_l 选择 {aᵢ,ₜ, bᵢ,ₜ ∈R Zₚ}₁≤ₜ≤ₙᵢ，并生成 {Aᵢ,ₜ, Bᵢ,ₜ}₁≤ₜ≤ₙᵢ 如下：
- 在 a_{i_l,t_l}, b_{i_l,t_l}, S_l 的情况下，设置 a_{i_l,t_l} = z₁, b_{i_l,t_l} = z₂，并在不知道 z₁ 和 z₂ 的情况下计算 A_{i_l,t_l} 和 B_{i_l,t_l}，方法如下：
$$
A_{i_l,t_l} = T_{i_l,t_l}^{a_{i_l,t_l}} = (g^{η_{i_l,t_l}})^{a_{i_l,t_l}} = (g^{z₁})^{η_{i_l,t_l}},
$$
$$
B_{i_l,t_l} = T_{i_l,t_l}^{b_{i_l,t_l}} = (g^{η_{i_l,t_l}})^{b_{i_l,t_l}} = (g^{z₂})^{η_{i_l,t_l}}.
$$
- 在其他情况下，S_l 以直接方式计算 Aᵢ,ₜ = Tᵢ,ₜ^{aᵢ,ₜ} 和 Bᵢ,ₜ = Tᵢ,ₜ^{bᵢ,ₜ}。

然后 PK = ⟨g, g₁, g₂, g₃, Y, {{Tᵢ,ₜ, Aᵢ,ₜ, Bᵢ,ₜ}₁≤ₜ≤ₙᵢ}₁≤ᵢ≤ₙ⟩ 并将 PK 发送给 A。

阶段1 ：A进行如下查询。
- 密钥生成查询 OKeyGen(L) ：假设 A向该查询提交 L = [L₁, L₂, …, Lₙ]。为了计算私钥 SK_L = ⟨D₀, D̃₀, ND₀, D ,₀, {D ,ᵢ, Dᵢ,₀, Dᵢ,₁, Dᵢ,₂}₁≤ᵢ≤ₙ⟩，S_l 考虑以下两种情况：
- 情况1 . L_{i_l} ≠ v_{i_l,t_l}：S_l 选择 r₀, Nd ∈R Zₚ 和 {rᵢ, řᵢ, δᵢ ∈R Zₚ}₁≤ᵢ≤ₙ，设置 r = Σᵢ₌₁ⁿ rᵢ，ř = Σᵢ₌₁ⁿ řᵢ，并计算秘密分量 [D₀, D̃₀, D*,₀] 如下：
$$
D₀ = g^{y–r}_2 = (g₂)^{z₁} g₂^{–r} = (g^{z₁})₂ g₂^{–r},
$$
$$
D̃₀ = g^{y–ř}_2 = (g₂)^{z₁} g₂^{–ř} = (g^{z₁})₂ g₂^{–ř},
$$
$$
ND₀ = g³^{Nd},
$$