数值分析求条件数

原创已于 2024-06-14 23:18:53 修改 · 3.1k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#数值分析 #条件数 #python

于 2019-11-06 16:40:29 首次发布

求条件数Cond（A）

本网所有内容文字、图片和音视频资料，版权均属个人所有，仅供个人呢学习参考，任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他方式复制发布/发表。举例说明：
eg4-4:求系数矩阵A的条件数。
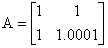
在这里插入图片描述

解：

求A的逆矩阵
分别对A的逆阵和A求行范数。
公式如下：
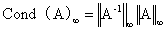
带入即可。

数值分析介绍

数值分析是数学的一个分支，主要研究使用数值计算方法解决数学问题的领域。以下是关于数值分析的详细解释：

定义与目的：
数值分析是研究用计算机求解数学计算问题的数值计算方法及其理论的学科。
数值分析的目的在于设计及分析一些计算的方式，可针对一些问题得到近似但够精确的结果。
应用领域：
数值分析在现代科学和工程领域中有着广泛的应用，包括但不限于：
工程领域：结构力学、电力系统、流体力学等。
金融领域：股票价格预测、风险评估、期权定价等。
自然科学领域：物理、化学、生物等。
主要方法：
直接法：利用固定次数的步骤求出问题的解，如高斯消去法、QR算法、单纯形法等。
迭代法：通过从一个初始估计出发寻找一系列近似解来解决问题的数学过程，如牛顿法、二分法、雅可比法等。迭代法通常用于求解大型矩阵代数问题。
数值分析算法：
方程组求解：高斯消元法、LU分解法等。
矩阵运算：矩阵乘法、矩阵求逆、特征值和特征向量计算等。
函数积分：数值积分方法（如梯形法则、辛普森法则）和自适应积分等。
离散化：
在数值分析中，经常需要将连续模型的问题转换为一个离散形式的问题，以便使用数值方法求解。这个过程称为离散化。
工具与软件：
MATLAB：用于数据分析、无线通信、图像处理等领域。
SPSS：统计产品与服务解决方案软件。
Excel：电子表格和数据处理软件，提供数据处理和分析功能。
R：统计计算和图形化软件环境，具有强大的数据分析能力。
Tableau：功能强大的数据可视化工具，提供丰富的可视化选项。
Python（NumPy、SciPy）：提供高性能的数值计算功能，以及各种优化和拟合函数。
SAS：专门用于统计分析和数据挖掘的商业软件。
数值分析的重要性：
数值分析为科学和工程领域提供了强大的计算工具，使得复杂问题的求解成为可能。
数值分析方法的准确性和效率直接影响到科学研究和工程设计的成果。
综上所述，数值分析是一个广泛应用于各个领域的数学分支，它通过研究和应用数值计算方法，为科学和工程领域提供了强大的计算支持。

条件数Cond（A）

条件数Cond(A)是一个数学概念，特别是在数值分析和线性代数中，它用于衡量矩阵A的“病态”程度，即矩阵在运算中的稳定性和误差敏感性。以下是关于条件数Cond(A)的详细解释：

定义：
条件数Cond(A)定义为矩阵A的范数与A的逆矩阵的范数的乘积。数学上，这可以表示为Cond(A) = ||A|| * ||A-1||，其中||A||表示矩阵A的某种范数，A-1表示A的逆矩阵。
范数的选择：
条件数Cond(A)的计算依赖于所使用的矩阵范数。常见的范数有1-范数、2-范数（也称为谱范数或欧几里得范数）和无穷大范数（也称为行和范数）。在MATLAB中，可以使用不同的参数来计算不同范数下的条件数，如cond(A,1)计算1-范数下的条件数，cond(A,2)或cond(A)计算2-范数下的条件数，cond(A,inf)计算无穷大范数下的条件数。
意义：
条件数Cond(A)的值反映了线性方程组Ax=b的解对b中的误差或不确定度的敏感性。当Cond(A)接近于1时，矩阵A被认为是“良态”的，即解的误差受到较小的影响；而当Cond(A)的值很大时，矩阵A被认为是“病态”的，解的误差会被放大，这可能导致数值计算的不稳定。
4.计算示例：
假设有一个矩阵A，其元素为[17,0,1,0,15; 23,5,7,14,16; 4,0,13,0,22; 10,12,19,21,3; 11,18,25,2,19]。在MATLAB中，使用命令cond(A,1)、cond(A,2)和cond(A,inf)可以分别计算出该矩阵在1-范数、2-范数和无穷大范数下的条件数。
实际应用：
在实际应用中，条件数Cond(A)被广泛用于评估算法的可靠性、选择最优算法和数据结构，以及在处理线性方程组、矩阵求逆、最小二乘问题、特征值和特征向量计算等数值计算问题中判断问题的难易程度和选择适当的求解方法。
综上所述，条件数Cond(A)是一个重要的数学工具，它可以帮助我们了解矩阵的稳定性和误差传播的程度，从而在实际应用中做出更准确的判断和决策。

数值分析求条件数，代码实现

条件数（Condition Number）在数值分析中是衡量矩阵病态性（ill-conditioning）的一个量度。它通常定义为矩阵的范数与其逆矩阵的范数的乘积，或者在某些情况下，是矩阵的谱范数与1范数的比值。这里，我将展示如何使用Python和NumPy库来计算矩阵的条件数。

以下是一个简单的例子，它计算了给定矩阵的条件数，这里我们使用谱范数（即矩阵的最大特征值）和1范数（即矩阵的列和范数）来计算条件数：

import numpy as np  
from scipy.linalg import norm, cond  
  
def compute_condition_number(A):  
    # 计算谱范数（最大奇异值）  
    spectral_norm = norm(A, ord='spec')  
      
    # 计算1范数（列和范数）  
    one_norm = norm(A, ord=1)  
      
    # 计算条件数  
    condition_number = spectral_norm * norm(np.linalg.inv(A), ord=1)  
      
    return condition_number  
  
# 示例矩阵  
A = np.array([[1, 2], [3, 4]])  
  
# 计算条件数  
condition_num = compute_condition_number(A)  
print("Condition number of A:", condition_num)  

# 另外，你也可以直接使用SciPy的cond函数来计算条件数  
# 注意：cond函数默认使用2范数（即谱范数）和无穷范数（即行和范数）的乘积来计算条件数  
condition_num_scipy = cond(A)  
print("Condition number of A (using SciPy):", condition_num_scipy)

但是，请注意，上面的compute_condition_number函数中的计算可能不是最优的，因为它需要显式地计算矩阵的逆。在实际应用中，我们通常会使用SciPy的cond函数，因为它使用了更高效的算法来计算条件数。

另外，条件数的计算可能会因为矩阵接近奇异（即不可逆）而失败。在这种情况下，计算逆矩阵的操作可能会抛出异常或产生不准确的结果。因此，在使用条件数之前，最好先检查矩阵是否可逆。

应用场景

条件数Cond(A)在多个应用场景中发挥着重要作用，特别是在数值分析和计算机科学领域。以下是关于条件数Cond(A)应用场景的清晰归纳：

评估矩阵的可逆性和解的稳定性：
条件数Cond(A)提供了一种衡量矩阵A的可逆性和解的稳定性的指标。当条件数较大时，输入中的微小变动可能会导致解的显著变化，系统的输出相对不稳定。相反，当条件数较小时，输入的微小变动对解的影响较小，系统的输出相对稳定。
评估数值算法的稳定性和可靠性：
条件数Cond(A)可用于评估数值算法的稳定性和可靠性，帮助选择合适的算法来解决线性系统、最小二乘问题等。较大的条件数可能提示问题输入的敏感性较高，可能需要通过增加数值精度、优化算法或者改变问题的表述方式来提高结果的准确性和稳定性。
评估矩阵的逆的稳定性：
对于矩阵A的逆A-1，条件数为cond(A) * cond(A-1)，即逆矩阵的条件数与原矩阵的条件数相乘。这一特性在求解线性系统的数值解时非常重要，较大的条件数可能导致误差放大，使得解的准确性下降。
线性方程组Ax=b的求解：
在求解线性方程组Ax=b时，条件数Cond(A)能够反映解x对b中微小变化的敏感性。如果A的条件数大，b的微小改变就能引起解x较大的改变，数值稳定性差；如果A的条件数小，b有微小的改变，x的改变也很微小，数值稳定性好。
数值优化问题：
在数值优化问题中，条件数Cond(A)可以用于评估目标函数的Hessian矩阵的性质，进而判断优化问题的难易程度和选择适当的优化算法。
图像处理：
在图像处理中，条件数Cond(A)可以用于评估图像变换矩阵（如旋转、缩放、仿射变换等）的稳定性，以确保图像变换后不会引入过多的噪声或失真。
控制系统：
在控制系统设计中，条件数Cond(A)可以用于评估系统矩阵A的稳定性，从而判断控制系统的稳定性和性能。
总结来说，条件数Cond(A)在多个领域中都发挥着重要作用，它不仅可以用于评估矩阵的可逆性和解的稳定性，还可以用于评估数值算法的稳定性和可靠性、评估矩阵的逆的稳定性、线性方程组的求解、数值优化问题、图像处理以及控制系统设计等多个方面。通过计算和分析条件数，我们可以更好地理解和处理与矩阵相关的问题，提高数值计算的准确性和稳定性。