在数学领域,希尔伯特空间又叫完备的内积空间,是有限维欧几里得空间的一个推广,使之不局限于实的情形和有限的维数,但又不失完备性(而不像一般的欧几里得空间那样破坏了完备性)。与欧几里得空间相仿,希尔伯特空间也是一个内积空间,其上有距离和角的概念(及由此引伸而来的正交性与垂直性的概念)。
定义
在一个复数向量空间 上的给定的内积
上的给定的内积 可以按照如下的方式导出一个范数(norm)
可以按照如下的方式导出一个范数(norm)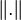 :
:
此空间称为是一个希尔伯特空间,如果其对于这个范数来说是完备的。这里的完备性是指,任何一个柯西列都收敛到此空间中的某个元素,即它们与某个元素的范数差的极限为 。任何一个希尔伯特空间都是巴拿赫空间,但是反之未必。
。任何一个希尔伯特空间都是巴拿赫空间,但是反之未必。
任何有限维内积空间(如欧几里得空间及其上的点积)都是希尔伯特空间。
内积可以帮助人们从“几何的”观点来研究希尔伯特空间,并使用有限维空间中的几何语言来描述希尔伯特空间。在所有的无穷维拓扑向量空间中,希尔伯特空间性质最好,也最接近有限维空间的情形。
傅立叶分析的一个重要目的是将一个给定的函数表示成一族给定的基底函数的和(可能是无穷和)。这个问题可以在希尔伯特空间中更抽象地描述为:任何一个希尔伯特空间都有一族标准正交基,而且每个希尔伯特空间中的元素都可以唯一地表示为这族基底中的元素或其倍数的和。
希尔伯特空间的一个中间概念是标准正交基,即其上的一族函数 满足:
满足:
有时也使用标准正交列或标准正交集指代。
标准正交基的一些实例:
- 集合(
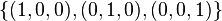 )
)





 本文详细介绍了希尔伯特空间的概念、定义、性质以及在数学领域内的应用,包括如何通过内积导出范数,希尔伯特空间与巴拿赫空间的区别,以及希尔伯特空间在傅立叶分析、标准正交基等方面的重要性。
本文详细介绍了希尔伯特空间的概念、定义、性质以及在数学领域内的应用,包括如何通过内积导出范数,希尔伯特空间与巴拿赫空间的区别,以及希尔伯特空间在傅立叶分析、标准正交基等方面的重要性。

 ,
, ,
,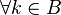 。
。 是这族基中的不同元素,那么
是这族基中的不同元素,那么 。
。















 1192
1192

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








