多输入变量的回归问题
一、向量化和多元线性回归
1. 基础概念
单变量线性回归:只有单个输入特征的线性回归模型
f
w
,
b
(
x
)
=
w
x
+
b
即:
f
(
x
)
f_{w,b}(x) = wx + b \quad \text{即:} f(x)
fw,b(x)=wx+b即:f(x)
多元线性回归:多元线性回归是一种统计模型,用于预测一个连续的目标变量(如房价),基于多个输入特征(如面积、房间数、地段等)之间的线性关系。
注:不要混淆“多元线性回归”和“multivariate regression”——后者是指多个输出变量,而这里是单输出、多输入。
f w ⃗ , b ( x ⃗ ) = w 1 x 1 + w 2 x 2 + … + w n x n + b = ∑ j = 1 n w j x j + b = w ⃗ ⋅ x ⃗ + b \begin{aligned} f_{\vec{w}, b}(\vec{x}) &= w_1 x_1 + w_2 x_2 + \ldots + w_n x_n + b \\ &= \sum_{j=1}^{n} w_j x_j + b \\ &= \vec{w} \cdot \vec{x} + b \end{aligned} fw,b(x)=w1x1+w2x2+…+wnxn+b=j=1∑nwjxj+b=w⋅x+b
- 常用术语解释
- w ⃗ = [ w 1 , w 2 , … , w n ] T \vec{w} = [w_1, w_2, \ldots, w_n]^T w=[w1,w2,…,wn]T: 参数向量,每个 w j w_j wj 表示对应特征对目标值的影响程度(权重)。
- x ⃗ = [ x 1 , x 2 , … , x n ] T \vec{x} = [x_1, x_2, \ldots, x_n]^T x=[x1,x2,…,xn]T: 输入特征向量,表示单个样本的多个属性。
- b b b: 偏置项(截距),可理解为“基础价格”或“默认值”。
- w ⃗ ⋅ x ⃗ \vec{w} \cdot \vec{x} w⋅x: 向量点积,即各特征与其权重的加权和。
- f w ⃗ , b ( x ⃗ ) f_{\vec{w}, b}(\vec{x}) fw,b(x): 模型输出,即对目标值的预测结果。
1.1 多维特征
是指将单个特征扩展到多个特征,每个样本由多个不同属性(特征)共同描述
- 如图为 将“房价预测”中的输入特征数量增加为4个:输入特征:房屋面积、卧室数量、房屋层数、房屋年龄
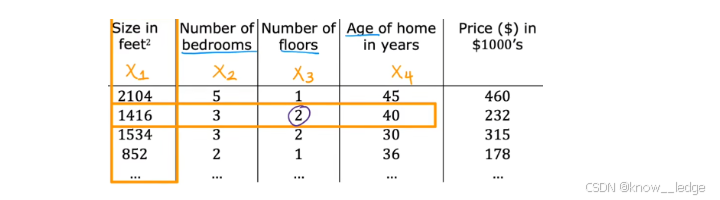
- 其线性模型表达式为:
f w ⃗ , b ( x ⃗ ) = w 1 x 1 + w 2 x 2 + … + w 4 x 4 + b \begin{aligned} f_{\vec{w}, b}(\vec{x}) &= w_1 x_1 + w_2 x_2 + \ldots + w_4 x_4 + b \\ \end{aligned} fw,b(x)=w1x1+w2x2+…+w4x4+b
- 这4个 w w w 数值可组成一个4维参数向量: w ⃗ = [ w 1 , w 2 , w 3 , w 4 ] T \vec{w} = [w_1, w_2,w_3, w_4]^T w=[w1,w2,w3,w4]T
- 这4个 x x x 数值可组成一个4维特征向量: x ⃗ = [ x 1 , x 2 , x 3 , x 4 ] T \vec{x} = [x_1, x_2, x_3, x_4]^T x=[x1,x2,x3,x4]T
图上圈出的 2 为第 3 个特征 x x x 的第 2 个样本值
1.2 向量化
向量化:是指将原本需要逐项线性计算的多个标量运算,转换为向量或矩阵形式进行并行处理的技术,其核心目的是:
- 避免显式使用 for 循环;
- 利用底层高度优化的线性代数库(如 NumPy、BLAS)实现高效并行计算;
- 使代码更简洁、可读性更强,并天然支持批量数据处理,机器学习中尽量使用向量化代码。

如图左一所示,在多元线性回归中,模型预测公式为:
f
w
⃗
,
b
(
x
⃗
)
=
w
1
x
1
+
w
2
x
2
+
…
+
w
n
x
n
+
b
\begin{aligned} f_{\vec{w}, b}(\vec{x}) &= w_1 x_1 + w_2 x_2 + \ldots + w_n x_n + b \\ \end{aligned}
fw,b(x)=w1x1+w2x2+…+wnxn+b
虽然数学上清晰,但若用传统编程方式实现,需写一个循环来累加每一项乘积:
# 非向量化实现(低效)
f = 0
for j in range(n):
f = f + w[j] * x[j]
f = f + b
而通过向量化,我们可以直接使用向量点积numpy.dot( )一步完成:
# 向量化实现(高效)
f = np.dot(w, x) + b
# 或写作:f = w @ x + b
- 这里的 np.dot(w, x) 计算的是 w ⃗ ⋅ x ⃗ \vec{w} \cdot \vec{x} w⋅x;
- 它不仅代码更短,更重要的是计算速度大幅提升,尤其在特征维度 n 较大时。
注:Optional Lab介绍了一些NumPy的语法。
2. 用于多元线性回归的梯度下降法
2.1 梯度下降法
了解基本概念之后,我们使用向量重写出梯度下降法的“向量”形式,进而迭代计算出模型参数:
线性回归模型: f w ⃗ , b ( x ⃗ ) = w ⃗ ⋅ x ⃗ + b 代价函数: min w ⃗ , b J ( w ⃗ , b ) = 1 2 m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 梯度下降: { w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) = w j − α m ∑ i = 1 m [ ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) ⋅ x j ( i ) ] b = b − α ∂ ∂ b J ( w ⃗ , b ) = b − α m ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) \begin{aligned} \text{线性回归模型:}\quad & f_{\vec{w}, b}(\vec{x}) = \vec{w} \cdot \vec{x} + b \\ \text{代价函数:}\quad & \min_{\vec{w}, b} J(\vec{w}, b) = \frac{1}{2m} \sum_{i=1}^{m} \left( f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)} \right)^2 \\ \text{梯度下降:}\quad & \left\{ \begin{aligned} w_j &= w_j - \alpha \frac{\partial}{\partial w_j} J(\vec{w}, b) \\ &= w_j - \frac{\alpha}{m} \sum_{i=1}^{m} \left[ (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \right] \\ \\ b &= b - \alpha \frac{\partial}{\partial b} J(\vec{w}, b) \\ &= b - \frac{\alpha}{m} \sum_{i=1}^{m} (f_{\vec{w}, b}(\vec{x}^{(i)}) - y^{(i)}) \end{aligned} \right. \end{aligned} 线性回归模型:代价函数:梯度下降:fw,b(x)=w⋅x+bw,bminJ(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2⎩ ⎨ ⎧wjb=wj−α∂wj∂J(w,b)=wj−mαi=1∑m[(fw,b(x(i))−y(i))⋅xj(i)]=b−α∂b∂J(w,b)=b−mαi=1∑m(fw,b(x(i))−y(i))
- 符号说明
代价函数:
- m m m:训练样本的总数。
- x ⃗ \vec{x} x:表示单个样本的所有特征,是一个一维向量(即特征向量)。
- f w ⃗ , b ( x ⃗ ( i ) ) f_{\vec{w}, b}(\vec{x}^{(i)}) fw,b(x(i)): 是模型对第 i i i 个样本的预测值,是一个标量。 y ( i ) y^{(i)} y(i):是第 i i i 个样本的真实标签,也是一个标量。
梯度下降:
- x j {x}_j xj:表示第 j j j 个特征, j j j 的取值范围为 j = 1 , … , n j = 1, \ldots, n j=1,…,n。
- x ⃗ ( i ) \vec{x}^{(i)} x(i):第 i i i 个训练样本的输入特征(一维向量), i i i 的取值范围为 i = 1 , … , m i = 1, \ldots, m i=1,…,m。
- x j ( i ) x_j^{(i)} xj(i):第 i i i 个训练样本的第 j j j 个特征,是单个数值。
注:若无特殊说明,所有的一维向量默认为列向量。
2.2 正规方程法
除了梯度下降法,还有一类求解模型参数的方法——正规方程法。该方法利用线性代数的知识,直接令代价函数的梯度 ∂ ∂ w ⃗ J ( w ⃗ , b ) = 0 ⃗ \frac{\partial}{\partial \vec{w}} J(\vec{w}, b) = \vec{0} ∂w∂J(w,b)=0,从而一步求出代价函数极小点对应的参数值:
w ⃗ = ( X ⃗ T X ⃗ ) − 1 X ⃗ T Y ⃗ \vec{w} = (\vec{X}^T \vec{X})^{-1} \vec{X}^T \vec{Y} w=(XTX)−1XTY
- X ⃗ \vec{X} X:全部的输入特征值,是一个二维矩阵(或称“数据矩阵”),每一行表示一个样本,每一列表示所有样本的单个特征。
- Y ⃗ \vec{Y} Y:全部的训练样本的目标值,是一维向量。
但是这种方法有两个主要缺点:
- 适用面小:仅适用于线性拟合,无法用于其他非线性模型。
- 计算规模不能太大:当特征数量很大时,矩阵的逆运算非常耗时,计算复杂度为 O ( n 3 ) O(n^3) O(n3)。
正规方程法通常已包含在机器学习函数库中,我们无需关心具体实现过程。对于大多数机器学习算法来说,梯度下降法仍然是推荐的参数优化方法。
二、使梯度下降法更快收敛的技巧
1. 特征缩放
- 特征缩放 可以使 梯度下降法 更快收敛
梯度下降法: { w j = w j − α ∂ ∂ w j J ( w ⃗ , b ) b = b − α ∂ ∂ b J ( w ⃗ , b ) \begin{aligned} \text{梯度下降法:}\quad & \left\{ \begin{aligned} w_j &= w_j - \alpha \frac{\partial}{\partial w_j} J(\vec{w}, b) \\ b &= b - \alpha \frac{\partial}{\partial b} J(\vec{w}, b) \\ \end{aligned} \right. \end{aligned} 梯度下降法:⎩ ⎨ ⎧wjb=wj−α∂wj∂J(w,b)=b−α∂b∂J(w,b)
- 原因:不同特征的取值范围差异很大,但所有特征对应的参数学习率 α \alpha α 是相同的。导致取值范围较小的特征参数“跟不上”大范围特征的变化,从而影响模型训练效率。
举例:房价预测

我们简化问题为两个输入特征:
price = w 1 x 1 + w 2 x 2 + b \text{price} = w_1 x_1 + w_2 x_2 + b price=w1x1+w2x2+b
其中:
- x 1 x_1 x1:房屋面积(单位:平方英尺),取值范围 300 ∼ 2000 300 \sim 2000 300∼2000
- x 2 x_2 x2:卧室数量,取值范围 0 ∼ 5 0 \sim 5 0∼5
示例数据:
- x 1 = 2000 x_1 = 2000 x1=2000, x 2 = 5 x_2 = 5 x2=5
- 真实价格:price = 500 k 500k 500k
现在考虑两种参数选择方案:
| 参数组合 | 预测结果 | 是否合理 |
|---|---|---|
| w 1 = 50 , w 2 = 0.1 , b = 50 w_1 = 50, w_2 = 0.1, b = 50 w1=50,w2=0.1,b=50 | price = 50 * 2000 + 0.1 * 5 + 50 = 100050.5 k 100050.5k 100050.5k | 完全不符 |
| w 1 = 0.1 , w 2 = 50 , b = 50 w_1 = 0.1, w_2 = 50, b = 50 w1=0.1,w2=50,b=50 | price = 0.1 * 2000 + 50 * 5 + 50 = 500 k 500k 500k | 正确匹配 |
结论:
虽然 x 1 x_1 x1 的取值范围更大,但它的权重 w 1 w_1 w1 应该更小;而 x 2 x_2 x2 的取值范围小,其权重 w 2 w_2 w2 应该更大。
否则,梯度下降会因尺度不一致而难以收敛。
1.1 特征归一化
为了使不同特征在相同尺度上竞争,我们对特征进行归一化处理,使得它们的取值范围大致相同,从而让梯度下降法更快收敛、更稳定。
- 如下图便给出了进行特征缩放前后的对比(散点图 vs 等高线图,以上方的房价预测为例):
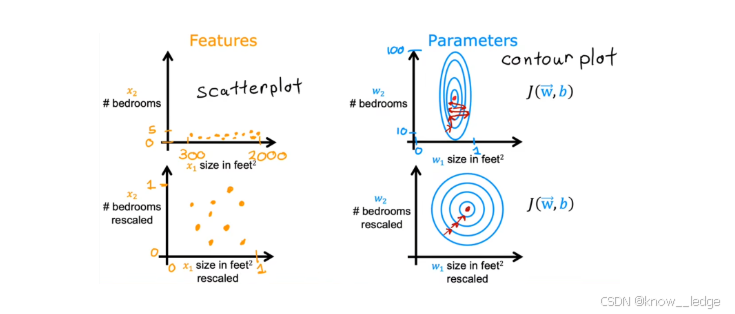
左两图是训练样本散点图;右两图是代价函数等高图。上两图对应特征缩放前;下两图对应特征缩放后。
- 缩放前的问题:
— 散点图呈“条形”分布,因为房屋面积( x 1 x_1 x1)范围大(300 ~ 2000),而卧室数量( x 2 x_2 x2)范围小(0 ~ 5)
— 代价函数等高线呈极窄的椭圆形,这是由于:对于范围较大的特征 x 1 x_1 x1,其对应参数 w 1 w_1 w1 的微小变化会导致代价函数剧烈波动,而 w 2 w_2 w2 的变化影响较小。在固定学习率下,梯度下降每走一步会在 w 1 w_1 w1 方向“跳得远”,在 w 2 w_2 w2 方向“动得少”,导致“反复横跳”;严重拖慢收敛速度,甚至无法收敛。- 缩放后的优势:
散点图分布较为均匀,并且等高图呈圆形。梯度下降法可以径直朝最小值迭代,减少迭代次数、更快的得到结果。
1.2 常用特征缩放(特征归一化)方法
- 为了实现特征值范围相近,常用以下三种方法:
1)除以最大值
将每个特征除以其最大值,使得所有特征值落在 [ 0 , 1 ] [0, 1] [0,1] 区间内。
x j ′ = x j max ( x j ) x_j' = \frac{x_j}{\max(x_j)} xj′=max(xj)xj
例如:
- x 1 x_1 x1(面积)范围:300 ~ 2000 → 缩放后:0.15 ~ 1
- x 2 x_2 x2(卧室数)范围:0 ~ 5 → 缩放后:0 ~ 1
优点:简单直观
缺点:对异常值敏感(如某个房子面积为 10000,则其他都接近 0)
2)均值归一化
将特征减去平均值,并除以范围,使值大致分布在 [ − 1 , 1 ] [-1, 1] [−1,1]。
x j ′ = x j − μ j max ( x j ) − min ( x j ) x_j' = \frac{x_j - \mu_j}{\max(x_j) - \min(x_j)} xj′=max(xj)−min(xj)xj−μj
假设:
- μ 1 = 600 \mu_1 = 600 μ1=600, max ( x 1 ) = 2000 \max(x_1) = 2000 max(x1)=2000, min ( x 1 ) = 300 \min(x_1) = 300 min(x1)=300 → x 1 ′ x_1' x1′ 范围: − 0.18 ∼ 0.82 -0.18 \sim 0.82 −0.18∼0.82
- μ 2 = 2.3 \mu_2 = 2.3 μ2=2.3, max ( x 2 ) = 5 \max(x_2) = 5 max(x2)=5, min ( x 2 ) = 0 \min(x_2) = 0 min(x2)=0 → x 2 ′ x_2' x2′ 范围: − 0.46 ∼ 0.54 -0.46 \sim 0.54 −0.46∼0.54
优点:中心对称,避免偏移
缺点:仍受极值影响
3)Z-score 归一化(推荐)
使用标准正态分布思想,将特征转换为平均值为 0、标准差为 1 的分布。
x j ′ = x j − μ j σ j x_j' = \frac{x_j - \mu_j}{\sigma_j} xj′=σjxj−μj
其中:
- 平均值: μ j = 1 m ∑ i = 0 m − 1 x j ( i ) \mu_j = \frac{1}{m} \sum_{i=0}^{m-1} x_j^{(i)} μj=m1∑i=0m−1xj(i)
- 方差: σ j 2 = 1 m ∑ i = 0 m − 1 ( x j ( i ) − μ j ) 2 \sigma_j^2 = \frac{1}{m} \sum_{i=0}^{m-1} (x_j^{(i)} - \mu_j)^2 σj2=m1∑i=0m−1(xj(i)−μj)2
- 标准差: σ j = σ j 2 \sigma_j = \sqrt{\sigma_j^2} σj=σj2
例如:
- x 1 x_1 x1: μ 1 = 600 \mu_1 = 600 μ1=600, σ 1 = 450 \sigma_1 = 450 σ1=450 → x 1 ′ x_1' x1′ 范围: − 0.67 ∼ 3.1 -0.67 \sim 3.1 −0.67∼3.1
- x 2 x_2 x2: μ 2 = 2.3 \mu_2 = 2.3 μ2=2.3, σ 2 = 1.4 \sigma_2 = 1.4 σ2=1.4 → x 2 ′ x_2' x2′ 范围: − 1.6 ∼ 1.9 -1.6 \sim 1.9 −1.6∼1.9
为什么推荐?
自然界大多数数据服从正态分布,Z-score 可使其标准化,提升模型稳定性。
- 如图为 Z-score 归一化的实际效果(归一化前后特征分布对比):
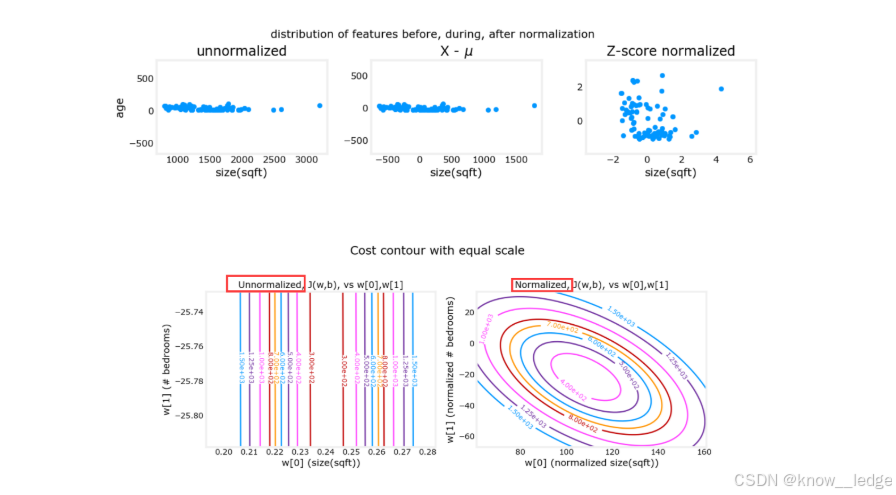
上面三个图的横纵坐标分别为两个特征:房屋面积 和 房屋年龄。
- 左图:未归一化 → 数据集中在左侧;
- 中图:减去均值 → 分布居中;
- 右图:Z-score 归一化 → 分布均匀且符合正态趋势。
下面两个图的横纵坐标同样为两个特征:房屋面积 和 卧室数量。
- 左图:未归一化 → 等高线呈细长椭圆;
- 右图:归一化后 → 等高线趋近圆形,梯度下降路径更直接。
结论:Z-score 归一化能有效改善数据分布和优化路径。
- 最后要说明一点,特征缩放后,只要所有特征值的范围在一个数量级就都可以接受,但若数量级明显不对等就需要 重新缩放。
2. 判断梯度下降是否收敛
2.1 收敛判断
学习曲线:是判断梯度下降算法是否收敛的重要工具。
它以迭代次数为横轴,代价函数值 J ( w ⃗ , b ) J(\vec{w}, b) J(w,b) 为纵轴,直观展示模型训练过程中的优化路径。
- 以下为正常收敛的学习曲线示意图(代价函数随迭代次数的变化趋势)
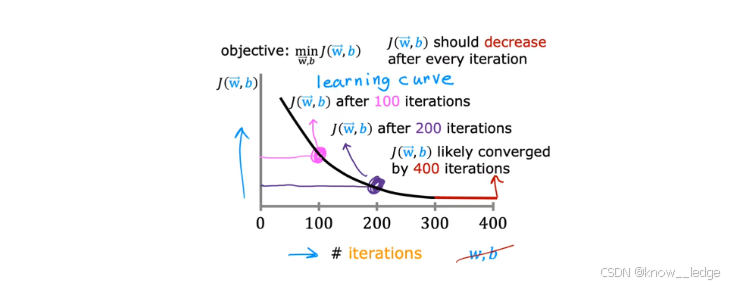
- 注意:
- 每次迭代后, J ( w ⃗ , b ) J(\vec{w}, b) J(w,b) 应该逐渐减小;
- 若某次迭代后代价函数反而上升,则说明算法未收敛;
- 当曲线趋于平坦(如红色段),表示已接近最小值,可认为算法收敛。
收敛判断标准
| 情况 | 表现 | 说明 |
|---|---|---|
| 正常情况 | 每次迭代后 J ( w ⃗ , b ) J(\vec{w}, b) J(w,b) 都下降 | 算法正在向最优解靠近 |
| 未收敛 | 某次迭代后 J ( w ⃗ , b ) J(\vec{w}, b) J(w,b) 变大 | 可能是学习率 α \alpha α 过大,导致“震荡” |
| 已收敛 | 曲线趋于平缓,几乎不再下降 | 可停止训练 |
自动收敛测试:
若连续两次迭代中,代价函数减少量满足:
∣ J ( t + 1 ) − J ( t ) ∣ ≤ ϵ = 1 0 − 3 \left| J^{(t+1)} - J^{(t)} \right| \leq \epsilon = 10^{-3} J(t+1)−J(t) ≤ϵ=10−3
则可认为已收敛。但 ϵ \epsilon ϵ 的选取依赖经验,因此仍建议结合学习曲线可视化进行判断。
提示:不同问题收敛速度差异很大——有些只需几十次迭代,有些需要上万次。无法提前预知时,使用学习曲线是最可靠的方法。
2.2 如何设置学习率
学习率 α \alpha α 是控制参数更新步长的关键超参数:
- α \alpha α 太小 → 收敛太慢;
- α \alpha α 太大 → 参数“跳过”最优解,甚至发散。
- 以下为不同学习率下的代价函数变化趋势图
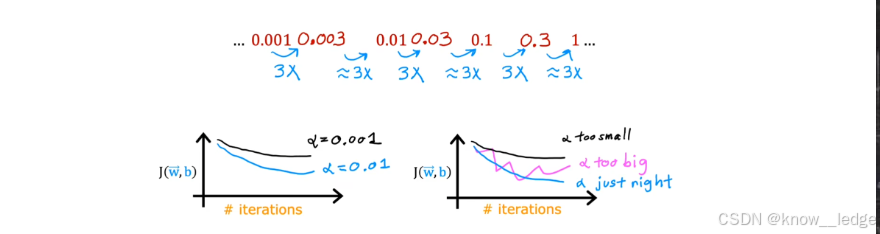
左图: α = 0.001 \alpha = 0.001 α=0.001 → 收敛极慢;
左图: α = 0.01 \alpha = 0.01 α=0.01 → 平稳下降;
右图: α = 0.3 \alpha = 0.3 α=0.3 → 起伏剧烈,可能不收敛。
正确的学习率选择策略
- 从较小值开始:例如 α = 0.001 \alpha = 0.001 α=0.001;
- 逐步增大:每次乘以 3 倍(如 0.001 → 0.003 → 0.01 → 0.03 → 0.1 → 0.3);
- 观察学习曲线:
- 若曲线平稳下降 → 继续增大;
- 若出现剧烈波动或上升 → 上一次的 α \alpha α 就是合适的最大值;
- 最终选择:略小于导致发散的那个值。
实践建议
- 验证代码逻辑正常:当 α \alpha α 极小时,代价函数应持续减小(即使很慢);
- 若代价函数起伏不定,可能是:
- 代码有 bug(如梯度方向写反);
- 学习率过大。
推荐做法:先用小 α \alpha α 快速验证逻辑正确性,再逐步调优。
三、特征工程
“特征工程”听起来陌生,实则是一套挑选、组合、变换原始特征的方法论。
其目标是通过领域知识或直觉设计出更符合现实规律的新特征,从而简化模型、提升预测精度。
注意:虽然
scikit-learn等广泛使用的开源机器学习库提供了强大功能,但理解原理比盲目调用函数更重要!
1. 选择合适的特征
最简单的特征工程就是创造更有意义的新特征。
示例:房屋占地面积
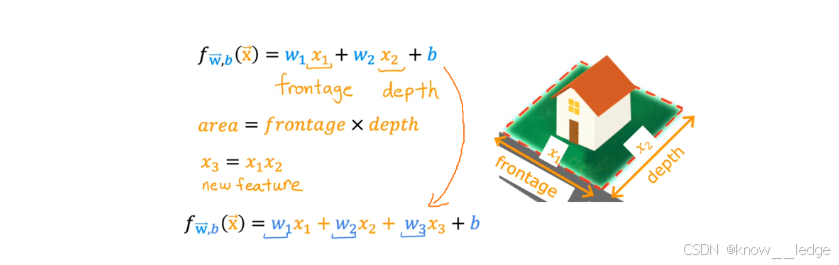
假设原始特征为:
- x 1 x_1 x1:frontage(地块长度)
- x 2 x_2 x2:depth(地块宽度)
虽然这两个特征有用,但占地面积(area)才是决定房价的核心因素。
于是构造新特征:
x
3
=
x
1
×
x
2
=
frontage
×
depth
x_3 = x_1 \times x_2 = \text{frontage} \times \text{depth}
x3=x1×x2=frontage×depth
模型变为:
f
w
⃗
,
b
(
x
⃗
)
=
w
1
x
1
+
w
2
x
2
+
w
3
x
3
+
b
f_{\vec{w}, b}(\vec{x}) = w_1 x_1 + w_2 x_2 + w_3 x_3 + b
fw,b(x)=w1x1+w2x2+w3x3+b
效果:新特征更贴近人类直觉,模型更容易拟合真实关系。
2. 多项式回归
另一种特征工程是对某个特征进行幂次变换,实现非线性拟合,即“多项式回归”。
- 以下图为多项式拟合 —— 二次、三次、开根号拟合(不同形式的非线性拟合效果对比)
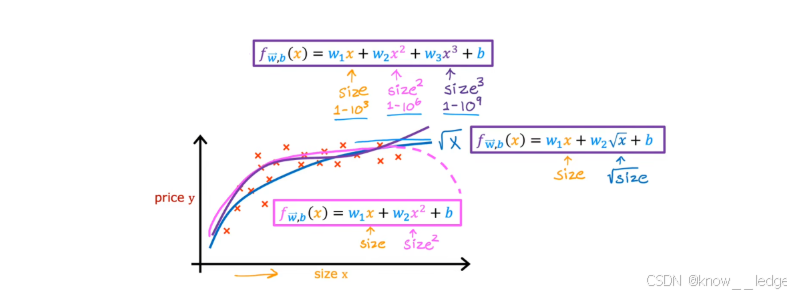
不同拟合方式分析:
| 拟合方式 | 优点 | 缺点 |
|---|---|---|
| 二次函数: f ( x ) = w 1 x + w 2 x 2 + b f(x) = w_1 x + w_2 x^2 + b f(x)=w1x+w2x2+b | 前半段拟合好 | 后期房价随面积下降,违背常识 |
| 三次函数: f ( x ) = w 1 x + w 2 x 2 + w 3 x 3 + b f(x) = w_1 x + w_2 x^2 + w_3 x^3 + b f(x)=w1x+w2x2+w3x3+b | 符合直觉 | 后期增长过快,可能过拟合 |
| 开根号拟合: f ( x ) = w 1 x + w 2 x + b f(x) = w_1 x + w_2 \sqrt{x} + b f(x)=w1x+w2x+b | 房价随面积缓慢上升,符合常识 | 需要合理设计特征形式 |
关键点:
- 幂次越高,特征缩放越重要(否则微小参数变化会导致代价函数剧烈波动);
- 特征工程需结合业务理解,不能仅靠数据驱动;
- 在后续课程中,我们将学习如何系统地挑选和设计特征,本节旨在让你理解“特征工程”的核心思想
- 总结
| 方法 | 目标 | 应用场景 |
|---|---|---|
| 特征选择 | 找到最有意义的原始特征 | 数据维度高时 |
| 特征组合 | 创造新特征(如面积 = 长 × 宽) | 有明确物理意义时 |
| 多项式回归 | 引入非线性关系 | 数据呈曲线趋势时 |
建议:在实际项目中,多尝试不同特征组合,结合学习曲线和验证集表现综合判断。





















 1515
1515

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








