吴恩达(机器学习)
注:前期需掌握知识点
python,数学基础
numpy,pandas,tensorflow 工具(可以边学边查)
python:掌握基础语法,numpy,pandas(b站莫烦老师的课)
tensorflow(DT算法工程师前钰)
数学掌握:
线性代数:向量、特征向量与特征值、范数、矩阵、运算。
高数:导数/微分/积分、概率论、梯度、泰勒展开公式。
一、机器学习:监督学习、无监督学习
1. 监督学习
给算法 “ 带答案的练习题 ”(输入 x + 正确输出 y),让它学会从 x 预测 y
- 输入 x 可以是一个或多个特征(比如面积 + 位置 + 房龄)
| 监督学习分为 | 解释 | 常用于 |
|---|---|---|
| 回归 | 从无限多个可能(连续数值)中预测一个数字 | 房价、温度、销售额 |
| 分类 | 从有限个类别(离散标签)中预测输入的类别 | “猫/狗”、“垃圾邮件/正常邮件” |
2. 无监督学习
数据仅包含输入x,没有输出标签y,算法需要在这些数据中找到某种结构、模式或者有趣的东西
| 无监督学习分为 | 解释 | 常用于 |
|---|---|---|
| 聚类 | 处理无标签数据并尝试自动将他们分组到簇里 | Google新闻,DNA,社群 |
| 异常检测 | 检测异常事件 | 金融系统欺诈检测 |
| 降维 | 将大量数据集压缩为小得多的数据集,同时尽可能少的丢失信息 |
二、Jupyter Notebook下载与使用
- 常用集成开发环境:IDE
| IDE | 特点及优势 |
|---|---|
| Jupyter Notebook | 基于网页端的开发模式,实时返回运行结果(适合学习) |
| Pycharm | 专为 Python 语言开发的IDE,提供了强大的代码编辑、调试、分析和重构功能 |
| VS code | 轻量级,有庞大的插件库(适用于各种类型的项目开发) |
| Vim | 经典的文本编辑器,高度定制性和键盘操作能力(Mac,Linux) |
1. 下载安装Jupyter Notebook
- 进入 Anaconda官网 进行下载
根据你的操作系统选择你要下载的 Anaconda
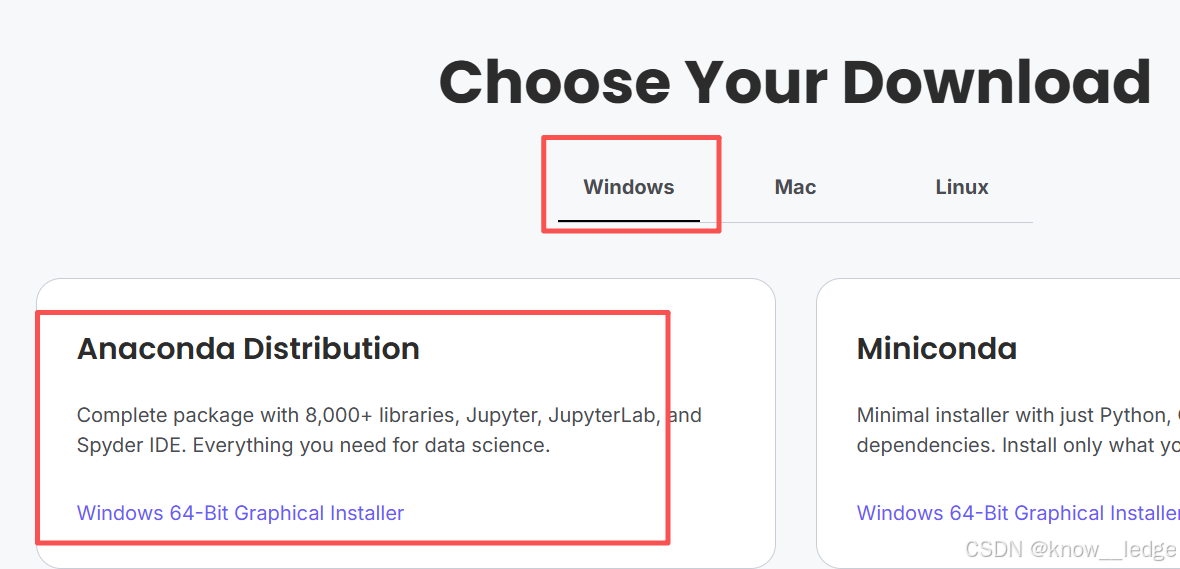
- 安装以及建议勾选
| 设置 | 建议勾选 |
|---|---|
| “Add Anaconda to my PATH” | 勾上(方便在命令行使用) |
| “Register Anaconda as my default Python” | 勾上(避免冲突) |
- 安装好后可直接搜索到 Jupyter Notebook (Anaconda自带)
- 选择浏览器打开
快速翻译英文练习题
- 建议两者搭配使用:
方法一:使用 Edge 可翻译英文内容,但从本地打开需手动设置
在Jupyter侧边栏右击鼠标,选择翻译为中文
方法二:使用有道翻译的截图功能
Ctrl + Alt + D

VS Code + Jupyter 插件
在 VS Code 插件库里直接安装 Jupyter 插件 (不支持翻译成中文)

2. Jupyter Notebook 使用方法速查表
| 类别 | 操作 / 功能 | 说明 |
|---|---|---|
| 界面导航 | 地址栏:http://localhost:8888 | 默认访问地址 |
| 创建新笔记本 | 点击右上角 New → Python 3 | 创建一个新的 .ipynb 文件 |
| 单元格类型 | Code(代码) | 默认类型,用于编写和运行 Python 代码 |
| Markdown | 用于写说明文字、公式、标题等(支持 LaTeX 和 HTML) | |
切换方式:快捷键 Esc 进入命令模式 | 按 M(Markdown) / Y(Code) | |
| 运行代码 | 快捷键:Shift + Enter | 运行当前单元格并跳到下一个 |
快捷键:Ctrl + Enter | 运行当前单元格但不跳转 | |
| 保存 | 自动保存 | 默认每 120 秒自动保存一次 |
| 常用快捷键 | Esc | 进入命令模式(可操作单元格) |
Enter | 进入编辑模式(可编辑单元格内容) | |
A | 在当前单元格上方插入新单元格 | |
B | 在当前单元格下方插入新单元格 | |
D + D(按两次 D) | 删除当前单元格 | |
Z | 撤销删除 | |
L | 显示/隐藏代码行号 | |
| 导出文件 | File → Save and Export Notebook As | 可导出为: • .py(纯 Python 脚本)• .html(网页)• .pdf(需 LaTeX)• .md(Markdown) |
| 关闭 Notebook | 关闭浏览器标签 | 不会终止内核! |
终端按 Ctrl + C 两次 | 安全退出 Jupyter 服务 | |
| 魔法命令 | %matplotlib inline | matplotlib绘制的图形直接显示在 Notebook 单元格的输出区域中 |
%load filename.py | 加载外部 Python 文件到单元格 | |
%timeit | 测试代码执行时间 (%%timeit 测试多行) | |
| 数学公式 | $...$ | 行内公式,公式嵌在文字中间,不换行 |
$$...$$ | 独立居中公式,公式单独成行,居中显示 |
Jupyter Notebook 文件导入方法速查表
| 类别 | 操作 / 功能 | 说明 |
|---|---|---|
| 文本文件 ( .txt, .log 等) | python with open(‘file.txt’, ‘r’, encoding=‘utf-8’) as f: content = f.read() | 读取整个文本内容(适合小文件) |
| CSV 文件 ( .csv) | python import pandas as pd df = pd.read_csv(‘data.csv’) | 自动解析表格,推荐方式 |
| JSON 文件 ( .json) | python import json with open(‘config.json’, ‘r’) as f: data = json.load(f) | 转为 Python dict/list |
| Excel 文件 ( .xlsx, .xls) | python df = pd.read_excel(‘report.xlsx’, sheet_name=‘Sheet1’) | 需安装 openpyxl(.xlsx)或 xlrd(旧版 .xls) |
| 快捷操作 | 将文件拖入 Jupyter 浏览器窗口 | 自动上传到 notebook 所在目录,可直接用文件名读取 |
三、线性回归模型
1. 线性回归模型
- 基本概念及常用术语
- 数据集:用于训练模型的数据集
- x x x:输入变量,也就是“特征值” ; y y y:输出变量,也就是“目标值”
- m m m:表示训练样本的数量
- ( x , y ) (x,y) (x,y):单个训练样本; ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i)):第 i i i 个训练样本,上标加括号是为了和求幂次区别开来
- y ^ \hat{y} y^:表示对 y y y 的估计或预测
-
【学习算法】根据输入的 数据集 得到一个函数模型【 f f f】,便可通过 f f f 来对输入 x x x 进行预测输出 y ^ \hat{y} y^
-
【线性回归模型】就是假设 函数模型 f f f 为一条直线,该模型可写为:
f w , b ( x ) = w x + b 即: f ( x ) f_{w,b}(x) = wx + b \quad \text{即:} f(x) fw,b(x)=wx+b即:f(x) -
举例:房价预测
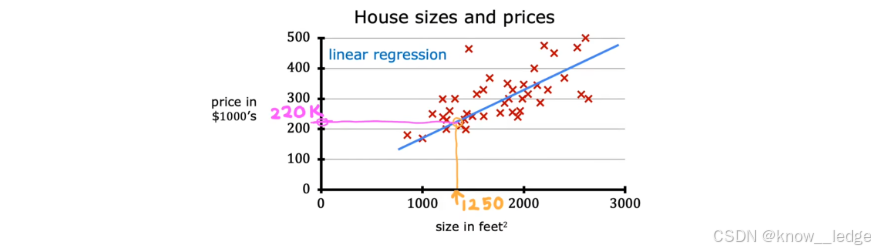
2. 代价函数
-
代价函数用于 衡量模型的好坏,帮助我们找到与训练数据最拟合的线
-
最简单、最常用的代价函数是 “ 平均误差代价函数 ” ,写法如下:
J ( w , b ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 J(w,b) = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 \\ \quad\quad\quad\quad\quad= \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 J(w,b)=2m1i=1∑m(y^(i)−y(i))2=2m1i=1∑m(fw,b(x(i))−y(i))2
- w 、 b w、b w、b:模型的参数(斜率,截距); i i i:训练样本的标号
- m m m:表示训练样本的数量
- y ( i ) y^{(i)} y(i):第 i i i 的样本的真实目标值; y ^ ( i ) \hat{y}^{(i)} y^(i):表示对 y ( i ) y^{(i)} y(i) 的预测目标值
- 除以 2 m 2 m 2m:按照惯例,机器学习中的平均代价函数会除以 2 m 2 m 2m 而非 m m m,这是为了使后续的计算更加简洁
为了方便理解 - - 最小化代价函数如何找到与训练数据最拟合的线,我们将该模型简化为二维模型:设置
f
w
,
b
(
x
)
=
w
x
+
b
f_{w,b}(x) = wx + b
fw,b(x)=wx+b 参数
b
=
0
b = 0
b=0,并假设训练数据只有三个点:
J
(
w
)
=
1
2
m
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
2
=
1
2
m
∑
i
=
1
m
(
f
w
(
x
(
i
)
)
−
y
(
i
)
)
2
J(w) = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 \\ \quad\quad\quad\quad\quad= \frac{1}{2m} \sum_{i=1}^{m} (f_{w}(x^{(i)}) - y^{(i)})^2
J(w)=2m1i=1∑m(y^(i)−y(i))2=2m1i=1∑m(fw(x(i))−y(i))2
- 显然在 w = 1 w = 1 w=1 处代价最小,直线也最拟合:
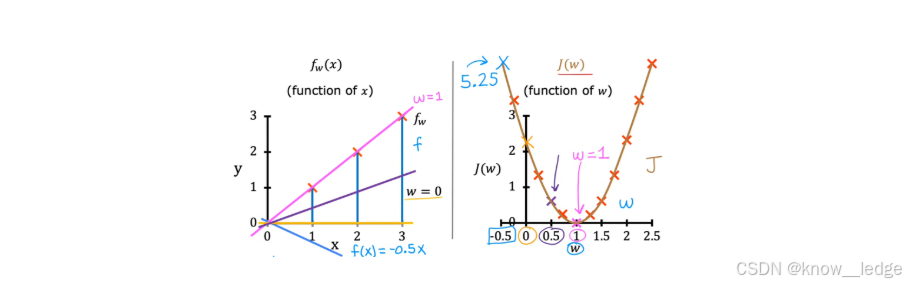
现在同时将 w w w 和 b b b 考虑在内,并引入更多的训练数据,便可以得到下面的代价函数三维示意图:
-
显然在中心点的位置,代价最小:
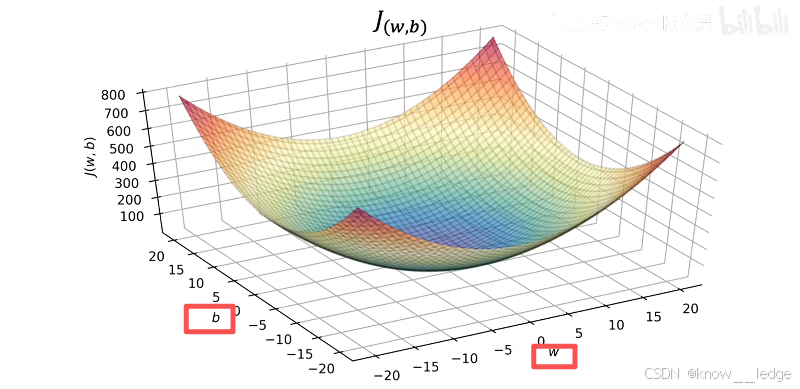
-
为了更好的将代价函数可视化,同时使用 “等高线图” 和 “3D图” 来展示不同的 w 、 b w、b w、b 所对应的不同代价 J ( w , b ) J(w,b) J(w,b)
-
越靠近等高线中心点的位置,代价越小:
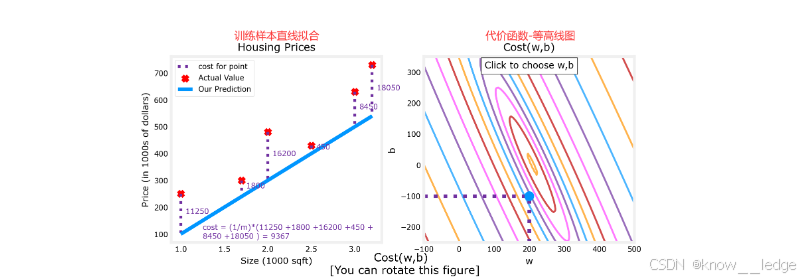
上述这种方法显然是不划算的,要画出这么细节的3d图需要大量计算 J ( w , b ) J(w,b) J(w,b)。使用梯度下降有效降低计算量
四、梯度下降法
用于线性回归的梯度下降
- 梯度下降是一种用于求解参数 w 、 b w、b w、b 值的算法,其目的是寻找某函数 (比如代价函数) 的最小值。
- 梯度下降,写法如下:
{ w = w − α ∂ ∂ w J ( w , b ) = w − α m ∑ i = 1 m [ ( f w , b ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ] b = b − α ∂ ∂ b J ( w , b ) = b − α m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) \left\{ \begin{aligned} w &= w - \alpha \frac{\partial}{\partial w} J(w, b) = w - \frac{\alpha}{m} \sum_{i=1}^{m} \left[ (f_{w,b}(x^{(i)}) - y^{(i)}) \cdot x^{(i)} \right] \\ b &= b - \alpha \frac{\partial}{\partial b} J(w, b) = b - \frac{\alpha}{m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)}) \end{aligned} \right. ⎩ ⎨ ⎧wb=w−α∂w∂J(w,b)=w−mαi=1∑m[(fw,b(x(i))−y(i))⋅x(i)]=b−α∂b∂J(w,b)=b−mαi=1∑m(fw,b(x(i))−y(i))
- w 、 b w、b w、b:模型的参数(斜率,截距); i i i:训练样本的标号
- α \alpha α:学习率,用于控制步长。通常为介于0~1之间的一个小的正数,如0.01
- ∂ ∂ w J ( w , b ) \frac{\partial}{\partial w} J(w, b) ∂w∂J(w,b):代价函数对 w w w 的偏导数
- ∂ ∂ b J ( w , b ) \frac{\partial}{\partial b} J(w, b) ∂b∂J(w,b):代价函数对 b b b 的偏导数
- 负梯度:负梯度就是 “下坡最快” ,往代价函数 J ( w , b ) J(w, b) J(w,b) 最小的方向走
- 直到 w w w 和 b b b 的负梯度都为 0 0 0 (或者 0 0 0的邻域内) ,即可认为找到了代价函数 J ( w , b ) J(w, b) J(w,b) 的最低点
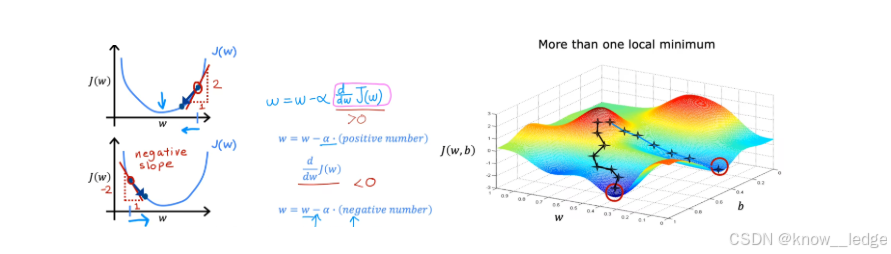
- 此图直观的展示了梯度下降的过程:
- 左侧图设置 J ( w , b ) J(w, b) J(w,b) 参数 b = 0 b = 0 b=0,当 w w w 在最低点的右侧, α ∂ ∂ b J ( w , b ) > 0 \alpha \frac{\partial}{\partial b} J(w, b)>0 α∂b∂J(w,b)>0,新的 w w w 将往左侧移动;同理,当 w w w 在最低点的左侧, α ∂ ∂ b J ( w , b ) < 0 \alpha \frac{\partial}{\partial b} J(w, b)<0 α∂b∂J(w,b)<0,新的 w w w 将往右侧移动。
- 右侧图进一步同时考虑了参数 b b b 和 w w w ,沿着 “负梯度” 快速下降,最终到达最低点。这个迭代的过程就是 “梯度下降”。

- 从 “等高线图” 的角度来看,梯度下降法的迭代过程可能如下图红色箭头所示,从起始点不断收敛到最小值,并且注意到这个过程也是越来越慢的。
注:w 和 b 的初始值
- w 和 b 的初始值是人为设定的,不是从数据中学来的
- 在线性回归中,最常用、最推荐的做法是:
w = 0
b = 0
| 项目 | 初始值怎么设定? | 为什么这样设? |
|---|---|---|
| w w w(权重) | 通常设为 0(或很小的随机数) | 线性回归的代价函数是凸函数,从任意起点都能收敛到全局最优解 |
| b b b(偏置) | 通常也设为 0 | 简单、对称、无需先验知识;同样因凸性保证收敛 |
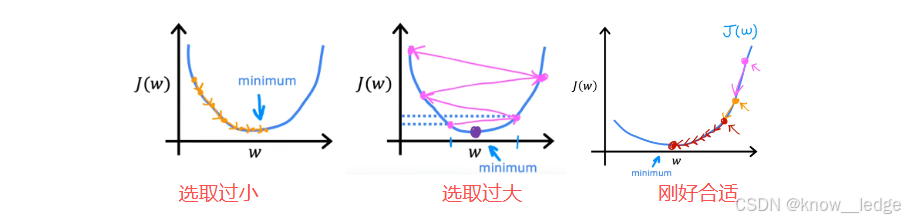
1)学习率 α \alpha α
- α \alpha α要选取的合适,不能太大也不能太小。
- 以求达到效果:越接近代价函数极小值,梯度越小,步长越来越小,最终实现收敛到最小值
2)多个极值点
- 代价函数尽量要选择凸函数,即:把平方误差项作为代价函数
- 平方误差项的代价函数,都是“凸函数”或“凸面”。
- 若代价函数非凸时,可能就会存在不止一个极值。不同的起始点,就会导致不同的收敛速度或极值。
3)批量梯度下降
由于在使用梯度下降法求解问题的过程中,每次迭代都会使用到所有的训练集数据计算代价函数及其梯度,所以这个梯度下降的过程称为 “ 批量梯度下降 ” 。
在其他数据更为复杂的模型中,为了简化梯度下降法的计算量,每次只使用训练集的子集
 吴恩达机器学习入门:线性回归与梯度下降
吴恩达机器学习入门:线性回归与梯度下降





















 1521
1521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








