本文介绍了向量距离的不同类型，包括欧氏距离、曼哈顿距离和切比雪夫距离，以及它们在不同场景的应用。此外，讨论了在数据分布的流形面上如何处理距离，并提出了贾卡尔距离和余弦相似度，尤其强调了余弦相似度在处理稀疏数据和评估相关性时的重要性。
这节要讲完距离基础部分就真完事了，不继续在基础中求得基础了，我发现也没人看
前文书写到要合理的设计特征是什么概念，我们再拿两个例子复习一下
比如一个卖车网站，上节我们讲过对物体识别可以用RGB来表示颜色的维度，那在卖车网站合适吗，其实是不合适的，因为，RGB潜在就有颜色大小区分，比如深蓝，浅蓝，有大小就会产生算法倾斜；那对于一个卖车网站，颜色就15种，你直接one-hot编码15个维度的向量就可以了
另外比如下图是一个企业级的社交网络简化版，我们就可以通过各个同事之间的关系，来通过one-hot来实现关系的表达
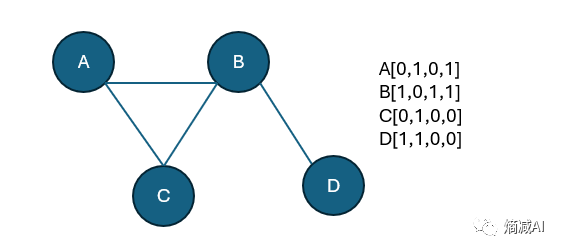
但是这个东西放微信或者微博里又基本扯淡了，因为上亿用户，所以另一个结论，特征设计，抛开量级不谈即使同一场景也是耍流氓
由上图也引出了我们今天的内容远近，比如AB和CD究竟谁和谁的关系最好，我们就拿向量的远近来衡量，这个远近就叫做向量距离！
如果两个向量通过距离进行相似度比较，那么以下几条是基本要求：
1-欧氏距离
我们都知道两点之间的距离，线段最短
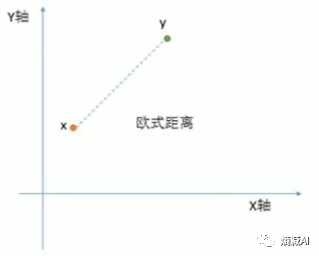
但是这是针对点来说的，可是我们面对的对象是两个向量做比较，比如：
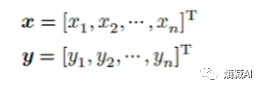
在这种情况下，我们就需要把两个向量的所有的维度分别做减法，然后进行平方，再做加和做开方，这样的目的是保证欧氏距离不会出现负数，满足基本要求里的非负性
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
