草履虫也能学会的强化学习系列（7）

更一期草履虫强化学习系列（书稿）

1.2.3 蒙特卡罗树搜索算法原理

在强化学习（Reinforcement Learning, RL）的语境下，蒙特卡洛（Monte Carlo, MC）方法通常被归类为无模型（Model-Free）方法。但是，我们也可以在基于模型（Model-Based）的框架下使用蒙特卡洛的思想。

1. 无模型（Model-Free）蒙特卡洛方法（这是最常见的用法）

核心思想：直接从与环境交互获得的完整经验片段（episodes）中学习价值函数（Value Function）或策略（Policy），而不需要学习或了解环境的动态模型（即状态转移概率 P(s'|s,a) 和奖励函数 R(s,a,s')）。

这俩举2个无模型的蒙特卡洛法的例子：

MC Prediction (预测):估计给定策略 π 下的状态价值 Vπ(s) 或动作价值 Qπ(s,a)。它通过在一个完整的 episode 结束后，计算从状态 s (或状态-动作对 (s,a)) 开始直到结束所获得的累积回报（Return）Gₜ，然后将多次 episode 中观测到的回报进行平均，作为价值的估计。

例如：V(s) ≈ average(Gₜ | Sₜ=s) （经过若干轮）

MC Control (控制):在估计动作价值 Qπ(s,a) 的基础上，通过不断改进策略来找到最优策略 π*。这通常涉及到广义策略迭代（Generalized Policy Iteration, GPI）的思想：根据当前的 Q 值贪婪地（或 ε-greedy地）更新策略，然后用新策略产生新的 episodes 来重新估计 Q 值。

REINFORCE：这个在下一章节详细展开讲。

特点：

不依赖环境模型。

只能从完整的 episodes 中学习（必须等到一个 episode 结束才能更新）。

对于非马尔可夫环境（non-Markovian environments）也可能有效（因为它不依赖于单步转移）。

方差通常较高，因为回报依赖于整个 episode 的随机性。

2. 基于模型（Model-Based）方法中使用蒙特卡洛思想

虽然标准的 MC 方法是无模型的，但我们可以在基于模型的框架下利用蒙特卡洛采样的思想：

核心思想：首先从与环境的交互中学习一个环境模型（估计 P 和 R）。然后，利用这个学习到的模型来模拟（simulate）大量的经验片段，再将无模型的蒙特卡洛方法（或其他方法如动态规划、时序差分）应用于这些模拟出的经验上，进行规划（Planning）或学习。

工作方式：

步骤 1: 模型学习（Model Learning）：通过与真实环境交互，收集数据 (s, a, r, s')，并使用这些数据来估计状态转移概率 P̂(s'|s,a) 和奖励函数 R̂(s,a)。

步骤 2: 规划/学习（Planning/Learning using the Model）：

蒙特卡洛规划 (Monte Carlo Planning / Simulation-Based Planning):使用学习到的模型 P̂ 和 R̂ 来生成大量的模拟 episodes。然后，对这些模拟的 episodes 应用标准的蒙特卡洛预测或控制方法来估计价值函数或优化策略。例如，从某个状态 s 开始，根据 P̂ 和 R̂ 模拟多条完整的轨迹，计算平均回报来估计 V(s)。

这种方法有时被称为基于模拟的规划（Simulation-Based Planning）。著名的例子是蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS），虽然它结合了树搜索和蒙特卡洛模拟，但其核心思想是在一个（隐式或显式的）模型或模拟器中通过采样来评估动作的好坏。

特点：

依赖于学习到的环境模型。

可以通过模拟产生大量经验，可能提高样本效率（Sample Efficiency），即用较少的真实环境交互达到好的效果。

学习效果受限于模型的准确性。如果模型不准确，规划/学习的结果可能会很差。

本节我们讨论有模型的蒙特卡洛方法，所以我们重点讲一下蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）。

首先我们先看一个概念，前向最大搜索树（Forward Search Expectimax Tree）

那么什么是前向搜索呢？

简单来说，前向搜索是一种在线规划（Online Planning）或决策时规划（Decision-Time Planning）的技术。它的核心思想是：当你需要决定在当前状态下采取哪个动作时，你才开始思考（搜索）未来的可能性，而不是提前计算好所有状态下的最优动作。

想象一下你在下棋：你不会在棋局开始前就计算出后面几百步所有可能局面下的最佳应对（这通常是不可能的）。相反，轮到你走棋时（即你在当前状态下），你会向前思考几步（向前搜索），评估各种可能的走法（动作）会导致什么样的局面（未来状态），以及这些局面最终可能带来的结果（价值/奖励），然后选择当前看起来最好的一步棋。这就是前向搜索的基本思路。

那么前向搜索树呢？

前向搜索算法通过“向前看”（Lookahead）来选择最佳动作 (Forward search algorithms select the best action by lookahead):

与动态规划（如价值迭代）或策略迭代等计算整个 MDP 所有状态的值或策略不同，前向搜索算法只关注当前状态 (s_t)。

它从当前状态出发，模拟（或者说“搜索”）未来可能发生的一系列状态和动作，评估不同初始动作可能带来的长期收益，然后选择当前看起来最好的那个动作。

它们构建一个以当前状态s_t 为根的搜索树。这个搜索过程的可视化就是一棵树。树的根节点就是当前的实际状态 s_t。

树的后续节点和分支代表了从s_t 开始，采取不同动作后可能遇到的后续状态以及在那些状态下可以采取的进一步动作。

使用 MDP 的模型进行向前看:

这是关键点，表明前向搜索是基于模型的（Model-Based）方法。

为了能够预测采取某个动作后会发生什么（即会转移到哪个或哪些后续状态，以及获得什么奖励），算法必须知道 MDP 的模型。这个模型通常包括：

状态转移概率 (Transition Probability):P(s' | s, a) - 在状态 s 采取动作 a 后，转移到状态 s' 的概率。

奖励函数 (Reward Function):R(s, a, s') - 在状态 s 采取动作 a 并转移到状态 s' 后获得的即时奖励。

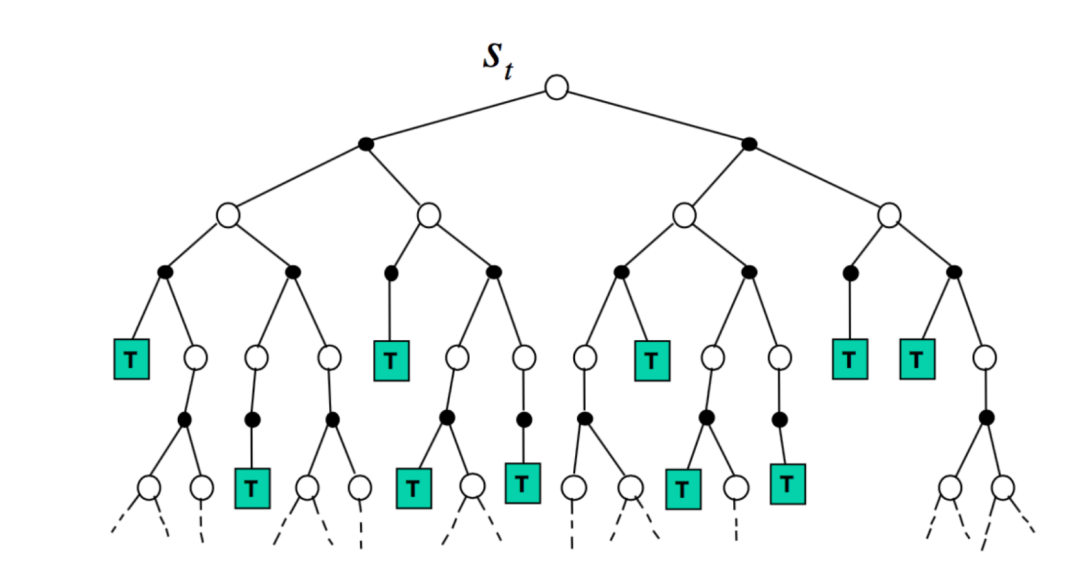
图示：期望最大树 (Expectimax Tree):

根节点 (s_t):代表当前状态，通常是一个“状态节点”（State Node），由代理（Agent）做决策。在图中用空心圆圈表示。

分支:从 s_t 出发的每个分支代表一个可行的动作。

黑色实心圆圈:代表“机会节点”（Chance Node）。当代理采取一个动作后，环境根据其内在的随机性（由转移概率 P(s'|s,a) 决定）选择下一个状态。可能有多个可能的后续状态，每个状态以一定的概率出现。

下一层的空心圆圈:代表采取动作并经过环境随机转移后到达的后续状态。在这些状态节点，代理又需要做决策。

树的结构:树通常是交替出现的：状态节点（代理选择动作，通常是最大化 Maximize 期望收益） -> 机会节点（环境根据概率决定结果，计算期望 Expectation 收益）。这就是“Expecti-Max”名字的由来。

叶子节点 (T):标记为 'T' 的绿色方块代表搜索达到的终止状态（Terminal state）或者预设的搜索深度限制。这些叶子节点有一个估计的价值（Utility），可能是终止奖励，或者是在达到最大深度时对该状态价值的一个估计（比如用一个启发式函数评估）。

回溯计算:期望最大算法通过从叶子节点向上回溯计算节点的价值：

在状态节点（空心圆），其价值是其所有子节点（机会节点）价值中的最大值(Max)。

在机会节点（实心圆），其价值是其所有子节点（状态节点）价值的期望值(Expectation)，即根据转移概率对子节点价值进行加权平均。

最终，根节点s_t 下每个动作对应的第一个机会节点的价值会被计算出来，代理选择那个具有最高价值的动作。

无需解决整个 MDP，只需解决从现在开始的子 MDP 。

这是前向搜索的一个主要优点，尤其是在状态空间非常大的情况下。算法不需要计算所有可能状态的最优策略或价值函数。它只在需要做决策时，针对当前状态s_t 构建一个有限深度的局部搜索树，解决这个“以 s_t 为根的子问题”。

这使得它在计算资源有限或状态空间过大而无法完全求解的情况下非常实用。

前向搜索 (Forward Search) 是一个更广泛的概念/框架:

它指的是一种在线规划（Online Planning）的策略：当需要做决策时，从当前状态出发，利用一个环境模型来模拟（“向前看”）未来的可能性，构建一个局部的搜索树，评估不同初始动作的价值，然后选择最好的那个动作。

它强调的是“在决策时、从当前状态向前看、使用模型”这个基本思想。

很多算法都可以归入前向搜索的范畴，比如：

期望最大搜索 (Expectimax Search):在树中显式地计算期望值和最大值（如上张幻灯片所示）。

有限深度 Minimax/Alpha-Beta 剪枝:在博弈论中常用，也是从当前状态向前看。

我更完了MCTS，估计还更几期再回头一期更 价值迭代和策略迭代还有mcts的代码

nested learning 下一次更