深度学习从入门到入土，基础知识篇四

1.什么是卷积

在深度学习网络中，卷积层用来提取数据的特征，通过不断地卷积，从而得到想要的特征，而卷积层的主要操作就是卷积，卷积的过程，通俗的讲就是一个加权求和的过程。在深度学习网络中，卷积操作也可以理解为一种特殊的线性变换，卷积的实现必不可少的就是卷积核，卷积核也称为滤波器，在输入的数据上进行滑动窗口式的卷积，从而实现局部数据特征的提取，实现特征的共享和抽象，从而使得网络对输入数据的变化更加鲁棒和准确。注意，在深度学习中，卷积核是可学习的，经过一定次数的迭代之后，才能更好的提取到稳定且需要的特征。（卷积是一种数学运算，具体来说是一种特殊的线性运算）

2. 卷积是如何进行特征提取的

卷积是一种按内积计算的方式，按照上图模式进行一定步长的卷积，具体的计算过程，可以参考下图，卷积之后得到一系列的特征图（feature map）,每一次卷积都会形成新的特征图，这些特征图表征着网络每一次迭代之后的结果。卷积通过卷积核在输入数据上滑动，计算每个位置上的加权和（有时还需要包含偏置），并可能应用激活函数，以生成输出的特征图。
2.1 选择卷积核：卷积核是一个可学习的参数矩阵，其大小（如3x3、5x5等）和数量（即输出特征图的通道数）是超参数。
2.2 滑动窗口：将卷积核在输入图像或特征图上按指定步长（stride）滑动，每次滑动都计算窗口内元素与卷积核的加权和。
2.3 计算加权和：对于每个滑动位置，将窗口内元素与卷积核对应位置的元素相乘后求和，并加上偏置项（如果有的话），得到输出特征图上对应位置的元素值。
2.4 添加激活函数：通常，卷积操作后会接一个激活函数（如ReLU），以增加网络的非线性特性。

3.卷积的重要参数

卷积核的参数主要包括卷积核的大小、卷积核通道数、卷积步长、填充等
3.1卷积核大小：卷积核的大小决定了卷积时的感受野大小，也就是每次卷积能够覆盖的数据范围，如3×3,5×5等；
3.2卷积核的通道数：对于输入图像，通道数指的是颜色通道数（如RGB图像的通道数为3）。对于卷积层，输出特征图的通道数由卷积核的数量决定，也就是说卷积核的通道数与输出特征图的通道数相等。
3.3 卷积的步长：卷积的步长就是卷积核每次所滑动的间隔距离，步长为1表示每次滑动一个像素，步长大于1则表示每次滑动多个像素；
3.4填充：在输入图像或特征图的边缘添加额外的零值，以控制输出特征图的尺寸。常见的填充方式有“valid”（无填充）和“same”（填充后输出尺寸与输入相同）

4.常见的卷积形式

4.1普通卷积：

普通卷积即平常所说的卷积，也就是标准2D卷积，按照设定好的卷积核大小，学习到的卷积权重，固定的卷积步长进行卷积，输出特征图的通道数就是卷积核的通道数。

4.2点卷积：

点卷积即卷积核大小为1×1的普通卷积，通常用于数据的整合或者改变特征图的深度，常用于降维或增加非线性；

4.3转置卷积（Transposed Convolution）

卷积不会增加输入的宽高，通常要么不变，要么减半，但转置卷积可以增大输入的宽高，实现的结果为上采样，如下所示，但需要注意的是转置卷积不是卷积的逆操作。

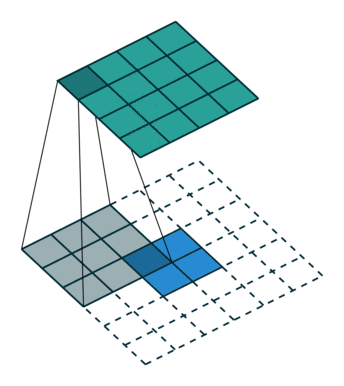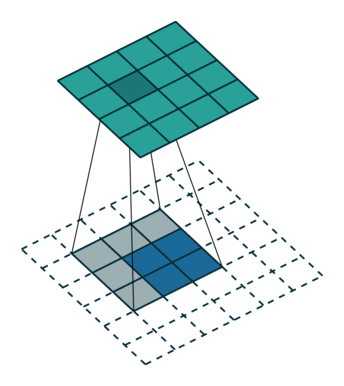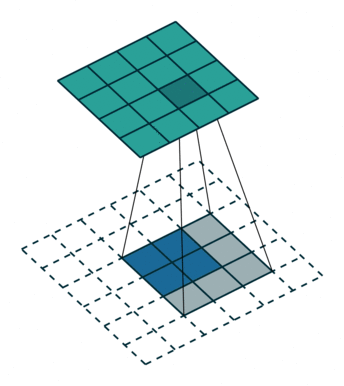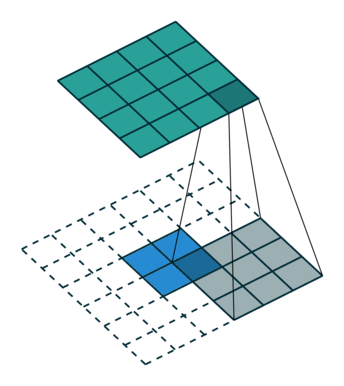
4.4深度可分离卷积

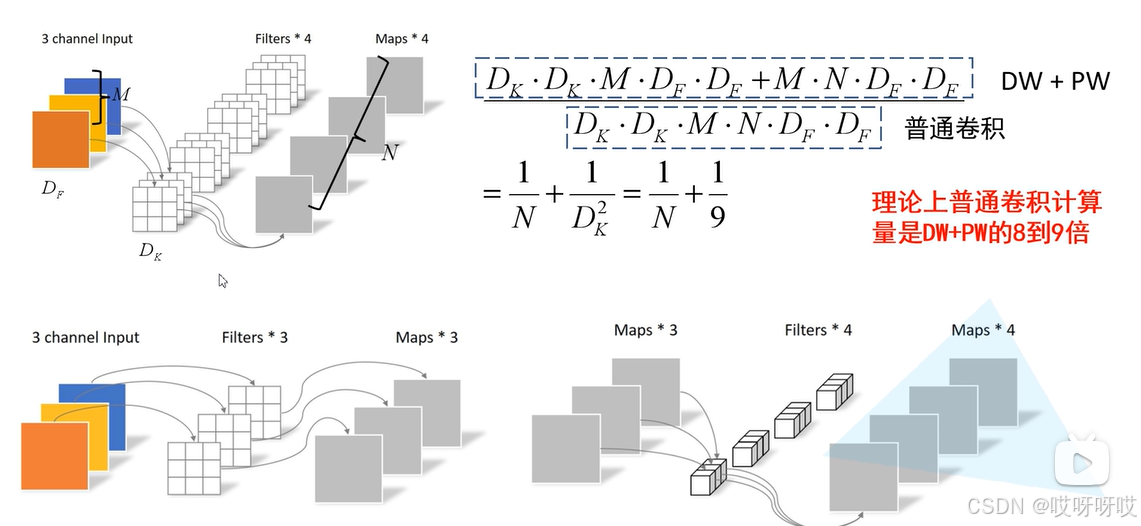
深度可分离卷积是一种特殊的卷积操作，用于减少卷积神经网络中的参数数量，从而提高计算效率和模型性能，深度可分离卷积由逐通道卷积（DW）和逐点卷积（PW）组成。
在逐通道卷积（DW）中，一个卷积核只负责一个通道，输入通道输与输出通道数完全相同，如下图所示

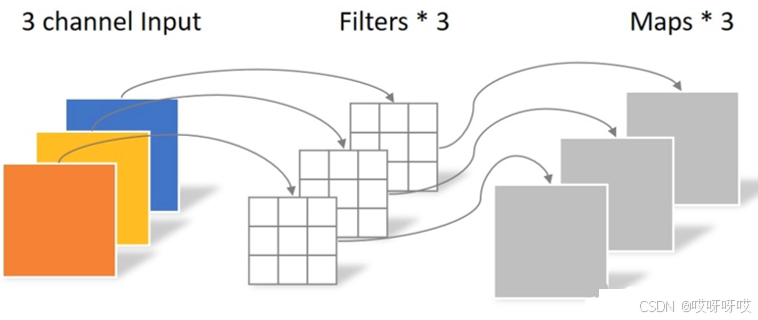
在逐通道卷积之后，进行逐点卷积，逐点卷积只改变输出特征图的通道数，并不改变输出特征图的大小，如下图所示

前面提到，深度可分离卷积可以降低卷积的计算量和参数量，实现高效快速的卷积操作。举例说明，假如输入一个大小为DFDFM，卷积核大小为DKDKN，则普通聚集的计算量为DF·DF·DK·DK·M·N，而深度可分离卷积（DW+PW）的计算量为DF·DF·DK·DK·M+
卷积层的参数数量计算公式：卷积核W x 卷积核H x 输入通道数 x 输出通道数)
卷积核计算量计算公式：卷积核W x 卷积核H x (图片W-卷积核W+1) x (图片H-卷积核H+1) x 输入通道数 x 输出通道数

4.5空洞卷积

空洞卷积可以实现感受野的增加，也称为膨胀卷积，简单来说就是在卷积核元素之间加入一些空格(零)来扩大卷积核的过程，可以在不改变特征图尺寸的情况下，显著增大感受野。对于捕捉较大感受野的任务有较大的溢出，空洞卷积的表示如下：

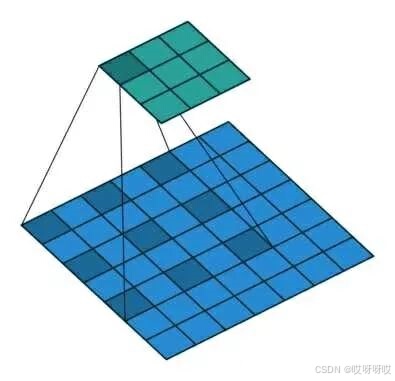
可以看出，空洞卷积其实是在普通卷积的基础上进行了扩张，在舍弃掉更中心的信息从而获得更大的感受野，获取更多的上下文信息，并且减少了一定的计算量（跳过了空洞区域）。但空洞卷积也存一定的局限性，如：
1.信息丢失与相关性减弱：由于空洞卷积是一种稀疏的采样方式，当多个空洞卷积层叠加时，可能会导致部分像素点从未被卷积核覆盖到，从而造成信息的丢失和远距离信息相关性的减弱。
2.网格效应：当空洞卷积的扩张率设置不当时（如连续使用相同的扩张率），可能会产生网格效应（gridding effect），即特征图上某些区域的信息被过度强调，而其他区域的信息则被忽略。这会影响分割和检测的准确性。
3.对小物体检测的挑战：虽然空洞卷积有助于提升小物体的检测能力，但过大的dilation rate可能会使得小物体在特征图上变得过于稀疏，从而难以被准确检测。因此，如何合理设置dilation rate以平衡大物体和小物体的检测性能是一个挑战。
4.设计复杂性：为了克服空洞卷积的缺点并充分发挥其优势，需要精心设计网络结构（如混合空洞卷积结构）和扩张率的分配策略。这增加了网络设计的复杂性和难度。

4.6分组卷积

分组卷积其实已经有过接触，在深度可分离卷积中，由逐通道卷积（DW）与点卷积（PW）卷积组成，而逐通道卷积实际就是分组卷积的极限化，将特征图的输入通道数分成语通道数相等的份数，每一个通道进行正常的卷积。分组卷积中将输入通道均分为若干份，每组进行正常卷积，实现卷积的参数量减少，并且隔绝了某些层之间的信息传递（如果是卷积之后单纯的叠加而不行逐点卷积）。

5.卷积的特点

1. 权值共享：在同一个卷积层内，所有的神经元共用一套参数，这就表示不管在哪个位置，都在提取相同的特征；
2. 特征不变：输入数据发生平移、旋转、缩放等变换时，卷积层能够提取相同的特征。这是由于卷积核的权重参数在滑动窗口的过程中保持不变。
3. 局部连接（局部感受野）：卷积层中的神经元只与输入的一部分区域相连，这种局部感受野的设计使得网络可以专注于检测输入中的局部模式。例如，在图像识别任务中，每个神经元只关注输入图像的一小块区域。

6.深度学习中卷积的三种模式（pytorch）

1. 全卷积（Full convolution）：输入特征图的每个点都与输出特征图的每个点进行卷积。
2. 有效卷积（Valid convolution）：只在输入特征图的边缘与输出特征图的对应点进行卷积。
3. 相同卷积（Same convolution）：保证输入特征图和输出特征图的大小保持一致，但是不一定是全部元素都参与卷积。