Windows游戏开发——观察坐标系的变化

原创

已于 2024-03-06 19:40:08 修改 · 532 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#windows #c++

于 2024-03-06 19:38:19 首次发布

本文介绍了在3D游戏中如何通过球坐标系控制观察坐标系的旋转和平移，利用鼠标移动改变摄像机视角，以及如何计算并更新观察矩阵以适应这些变化。开发者可以参考这些技术在DirectX12编程中实现游戏视图的动态调整。

1.主体思路

对于3D游戏中,世界-观察坐标系的具体思路可看我的这篇文章-坐标系的转化。
3D游戏物体的改变通过矩阵的线性变化方式,左乘最终变化矩阵(列向量的情况下).对于最终变化矩阵,是由世界矩阵(对于世界坐标系),观察矩阵(对应观察坐标系),投影矩阵(在3D空间到2D屏幕的投影变化)三者组合而来的。在一些游戏场景中,世界矩阵与投影矩阵在初始化时便被定义好了,而我们在游戏中改变的通常是观察坐标系,如CS中,鼠标移动对应着观察坐标系的旋转变化,键盘W触发的便是观察坐标系的平移变化。
在开发上,我们改变观察坐标系的方式有许多种,本文章介绍的角度是从球坐标系(3维的极坐标系)为出发点从而得出最终的观察坐标系。

2.球坐标系

通过球坐标系的坐标变化,然后转换为笛卡尔坐标系,从而得到观察坐标系。
首先球坐标系的表示如下:
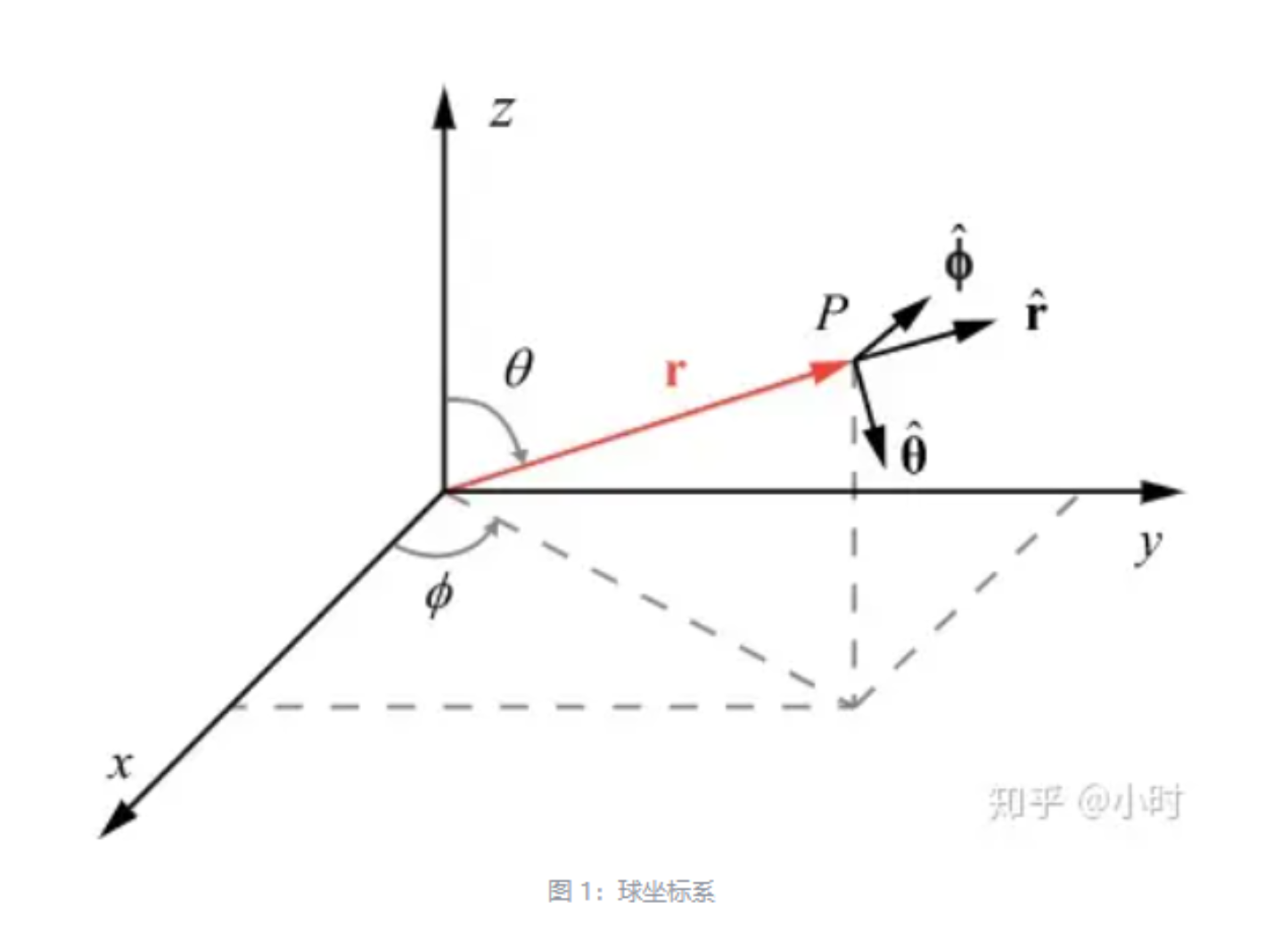
在这里插入图片描述
球坐标系的(r,θ,Φ)可比笛卡尔坐标系更契合3D坐标系的旋转平移缩放变化。
代码初始化定义:

	//世界,观察,投影坐标系定义为4x4的单位矩阵
	XMFLOAT4X4 mWorld = MathHelper::Identity4x4();	
	XMFLOAT4X4 mView = MathHelper::Identity4x4();
	XMFLOAT4X4 mProj = MathHelper::Identity4x4();
	
	//(θ,Φ,r)
	float mTheta = 1.5f * XM_PI; 	//θ
	float mPhi = XM_PIDIV4;			//Φ
	float mRadius = 5.0f;			//r半径  
	POINT mLastMousePos;			//鼠标的上一次位置

球坐标系的改变代码如下:

//(x,y)为鼠标的当前位置
void InitDirect3DApp::OnMouseMove(WPARAM btnState, int x, int y) {
   
   
	if ((btnState & MK_LBUTTON) != 0)
	{
   
   
		//使每个像素旋转1/4度