FCM算法

1.FCM模糊聚类算法

如何理解模糊聚类中的“模糊”二字？
假设有两个集合分别是A、B，有一成员a，传统的分类概念a要么属于A要么属于B，在模糊聚类的概念中a可以0.3属于A，0.7属于B，这就是其中的“模糊”概念。

模糊聚类分析有两种基本方法：系统聚类法和逐步聚类法。

系统聚类法个人理解类似于密度聚类算法，逐步聚类法类是中心点聚类法。

逐步聚类法是一种基于模糊划分的模糊聚类分析法。它是预先确定好待分类的样本应分成几类，然后按照最优原则进行在分类，经多次迭代直到分类比较合理为止。
在分类过程中可认为某个样本以某一隶属度隶属某一类，又以某一隶属度隶属于另一类。这样，样本就不是明确的属于或不属于某一类。若样本集有n个样本要分成c类，则他的模糊划分矩阵为c×n。
该矩阵有如下特性：
①. 每一样本属于各类的隶属度之和为1。
②. 每一类模糊子集都不是空集。
模糊C-均值(FCM)算法应用最广泛且成功，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而对样本进行自动分类。

2.FCM算法原理

假设我们有数据集X， 对X中的数据进行分c个类，对应的c类中心有$C_i$,每个样本$X_{ij}$属于某个类$C_j$的隶属度定为$U_{ij}$，则定义一个FCM目标函数及其约束条件为：
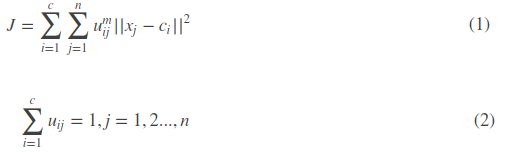目标函数式1由相应样本的隶属度与该样本到各类中心距离相乘组成，m为一个隶属度因子，一般为2。
目标函数J越小越好，则
程序一开始的时候我们会随机生成一个 U i j U_{ij}