B树（B-tree）

数据库的索引为什么使用树结构存储？

树的查询效率高，且可以保持有序。

从算法逻辑上来说，二叉查找树的查找速度和比较次数都是最小的,

那索引为什么不使用二叉查找树？

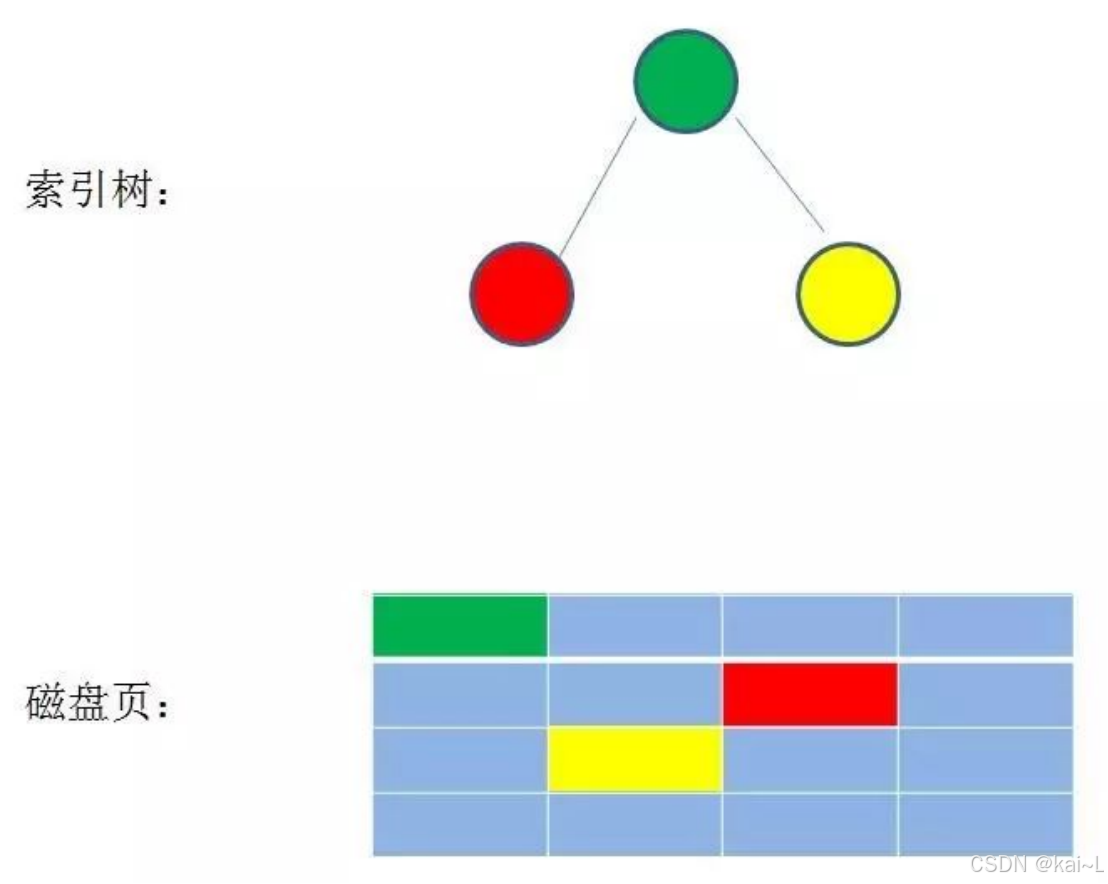
磁盘IO问题。数据库索引存储在磁盘上，数据量大的时候可能几个g或者更多。

当我们利用索引查询的时候，不能把整个索引全部加载到内存。能做的只有逐一加载磁盘页，

磁盘页对应着索引树的节点

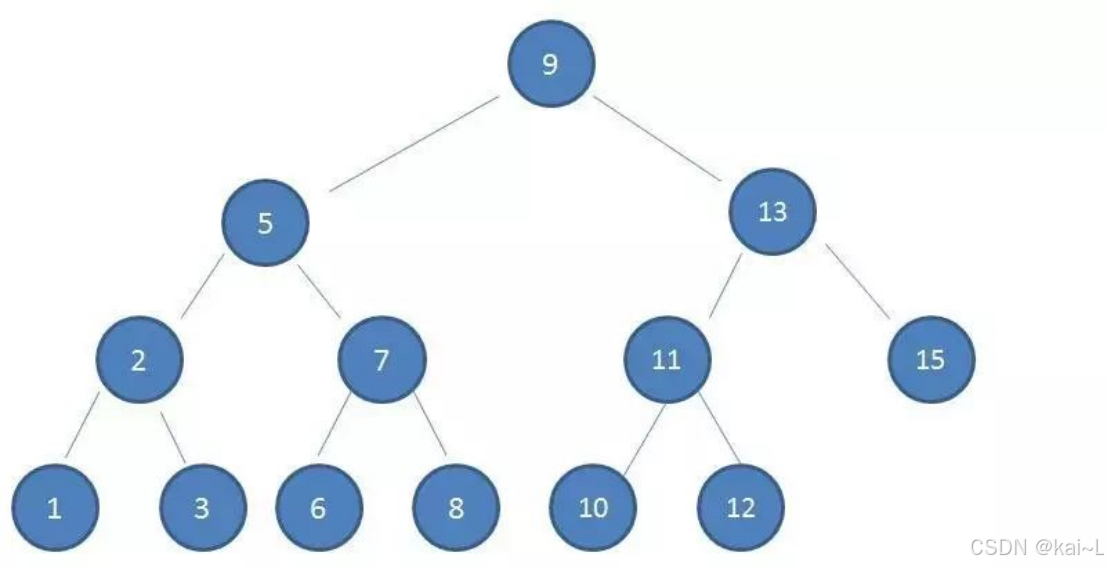
当利用二分查找树作为索引结构，树的高度为4，查找值10，情形如下：

二叉查找树的结构：

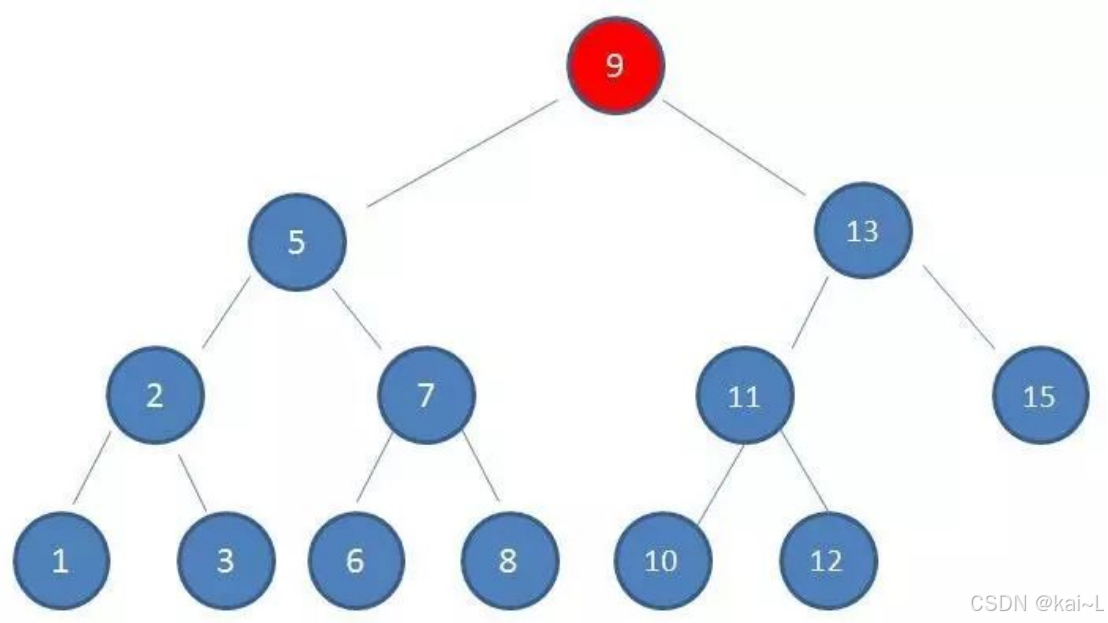
第1次磁盘IO：

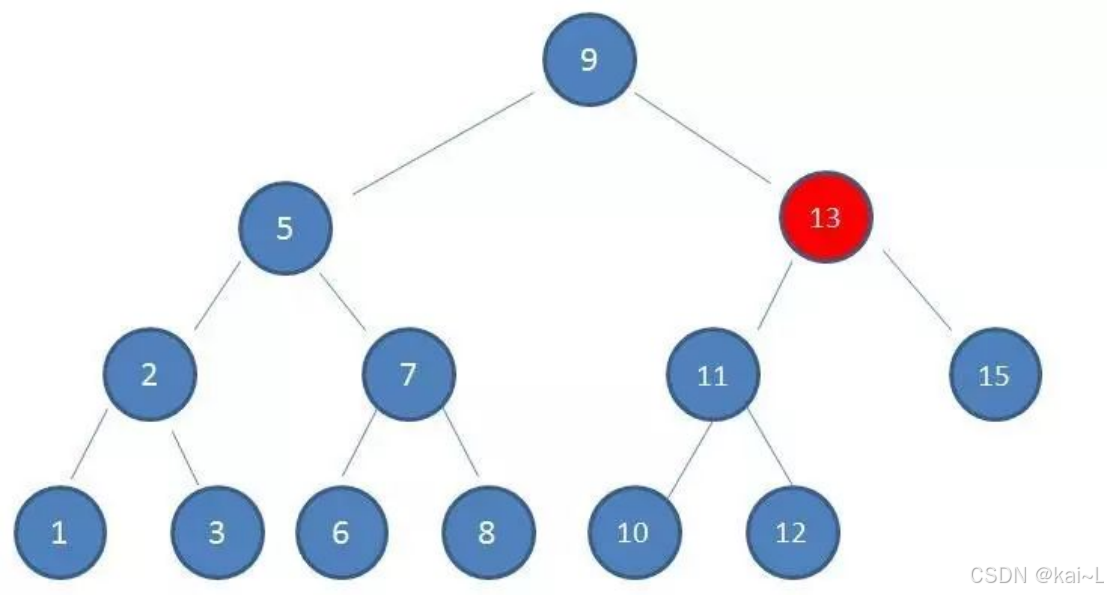
第2次磁盘IO：

第3次磁盘IO：

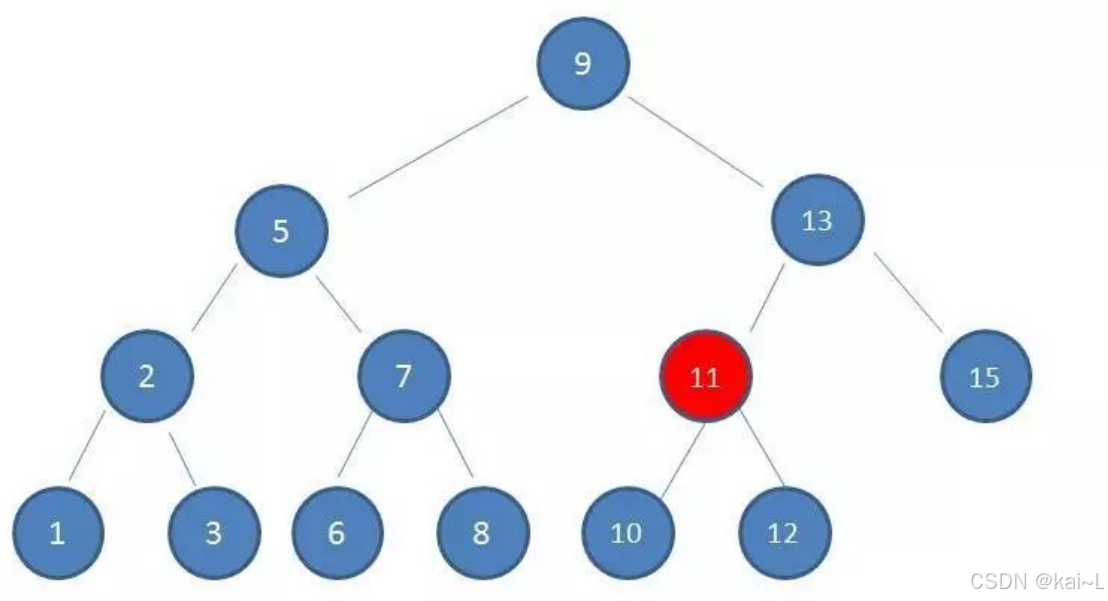
第4次磁盘IO：

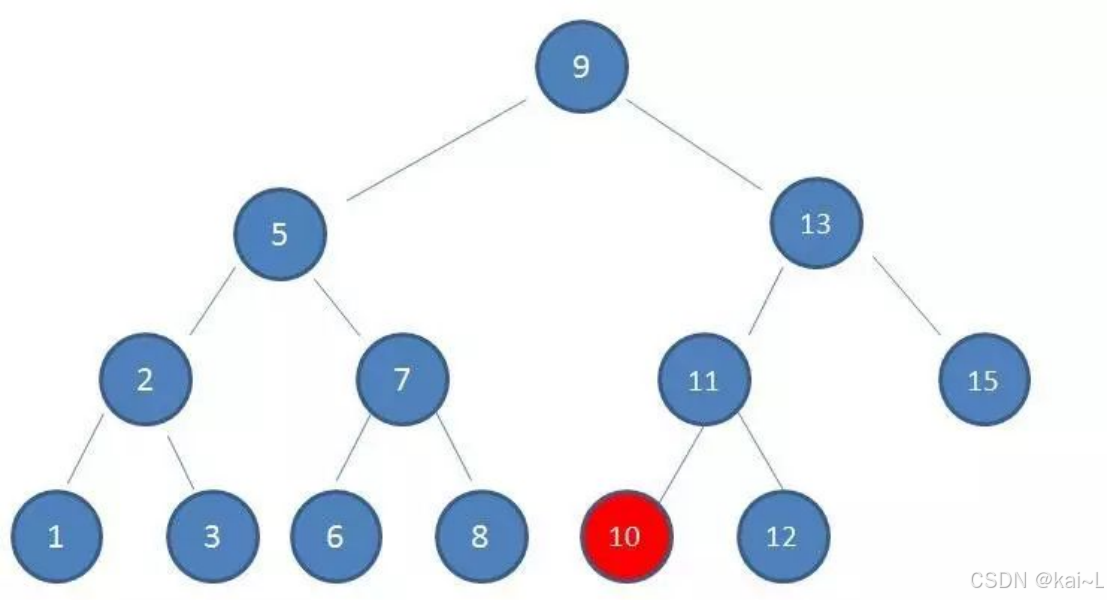
这时会发现磁盘IO次数是4，索引树高度也为4，

最坏情况下磁盘IO次数等于索引树高度（到叶子）。

为了减少磁盘IO操作，需要把“瘦高”的树形结构变得“矮胖”。也是B树的特征之一。

B树是一种多路平衡查找树，每个节点最多包含k个孩子，k大小取决于磁盘页大小。

下面来具体介绍一下B-树（Balance Tree），一个m阶的B树具有如下几个特征：

1.根结点至少有两个子女。

2.每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m

3.每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m

4.所有的叶子结点都位于同一层。

5.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

三阶b-树为例：

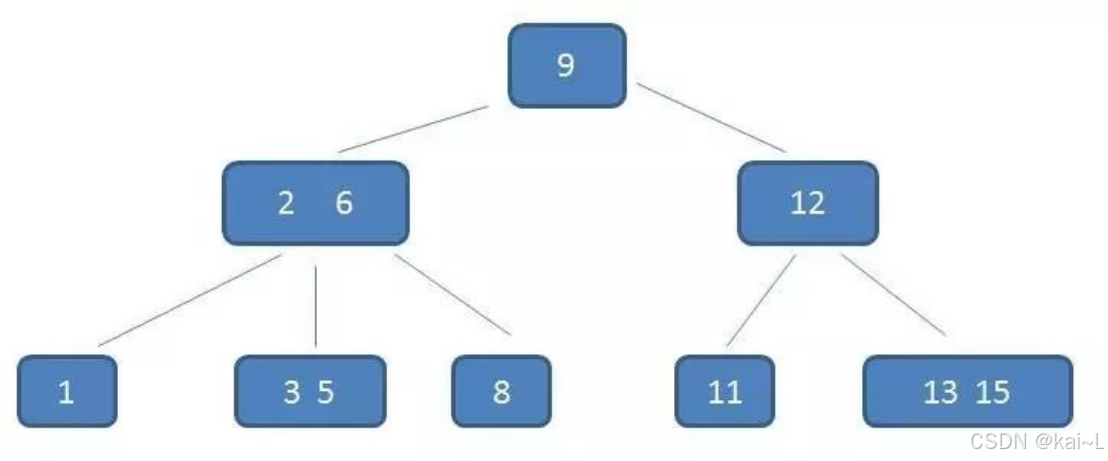
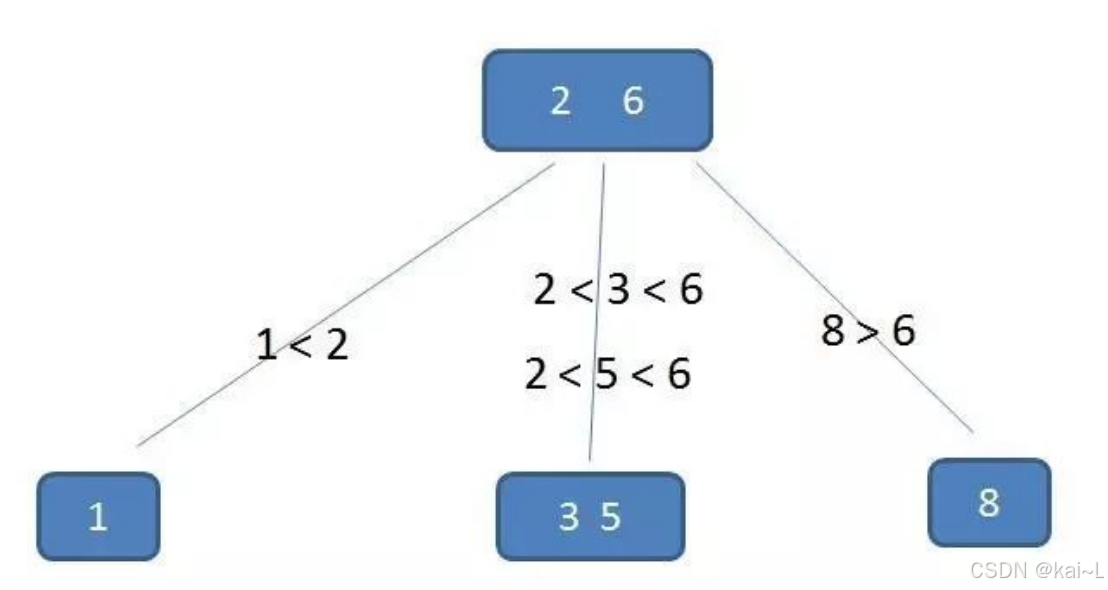
加入查询5，查询过程如下

第1次磁盘IO：

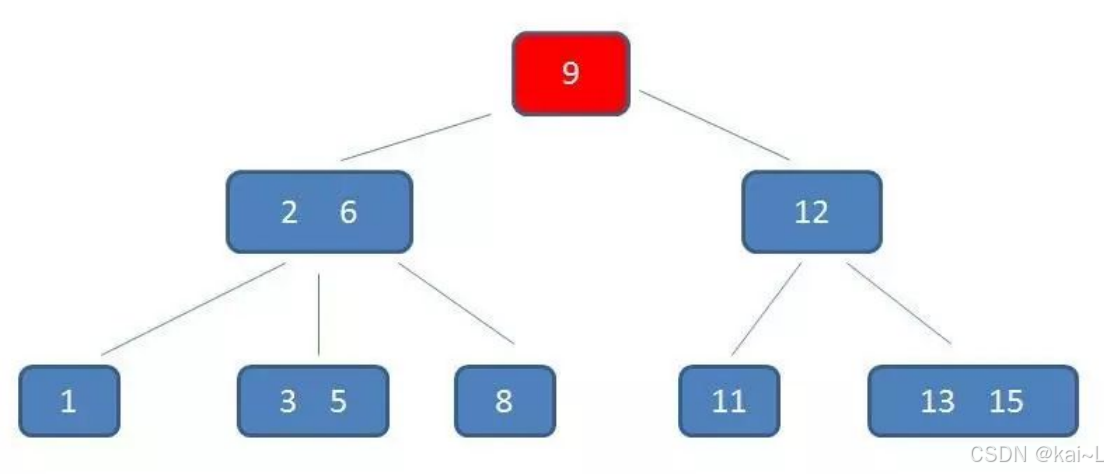
在内存中定位（和9比较）：

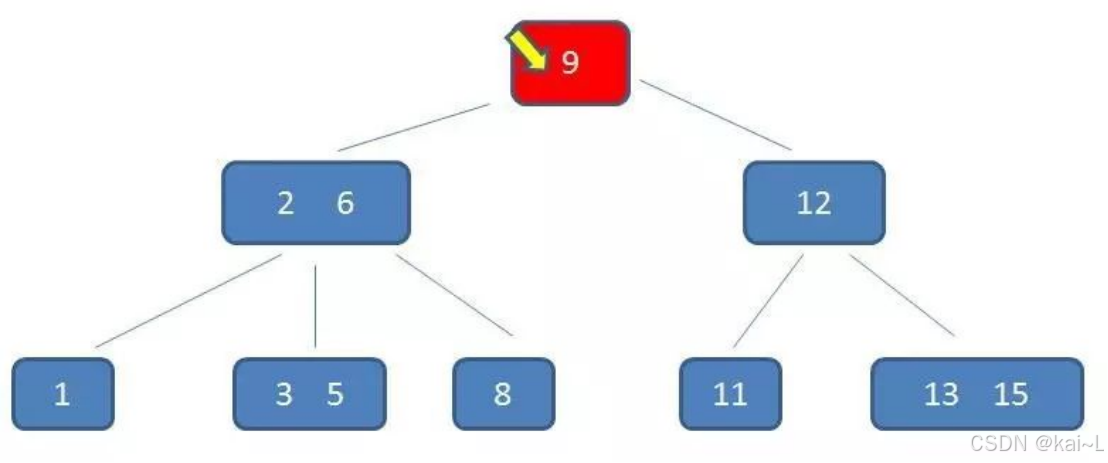
第2次磁盘IO：

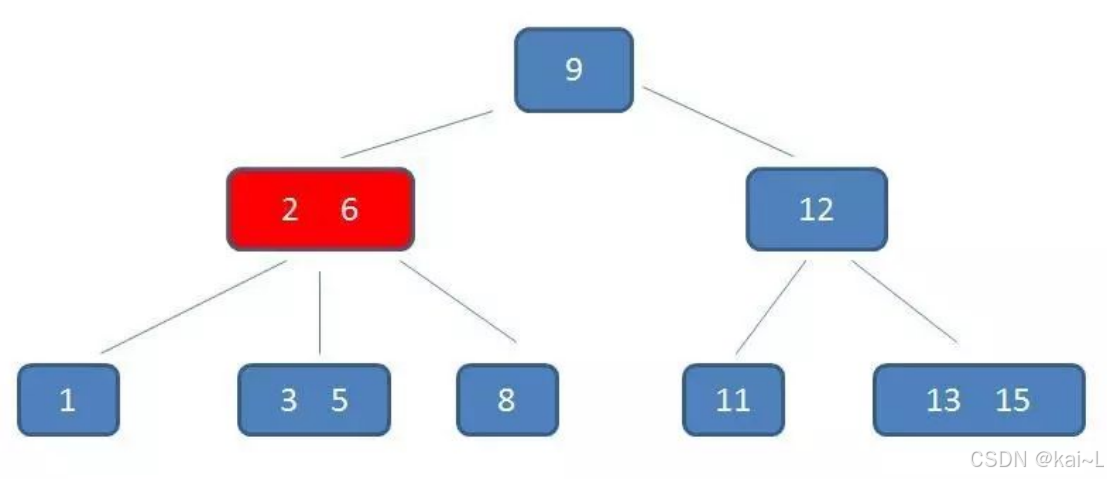
在内存中定位（和2，6比较）：

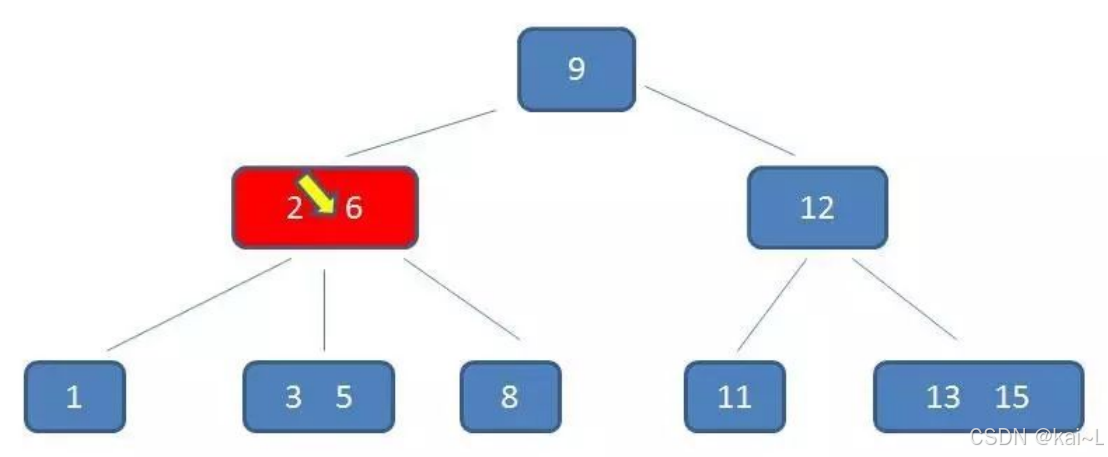
第3次磁盘IO：

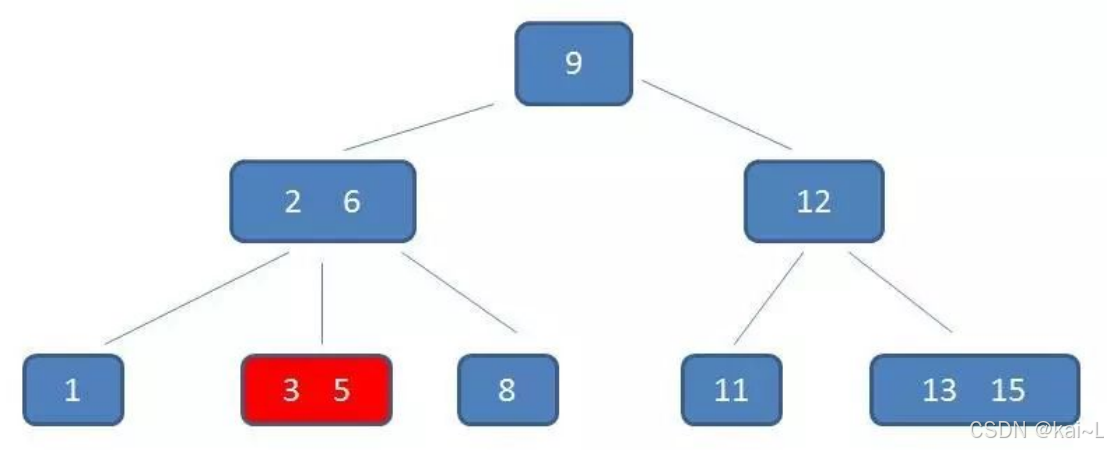
在内存中定位（和3，5比较）：

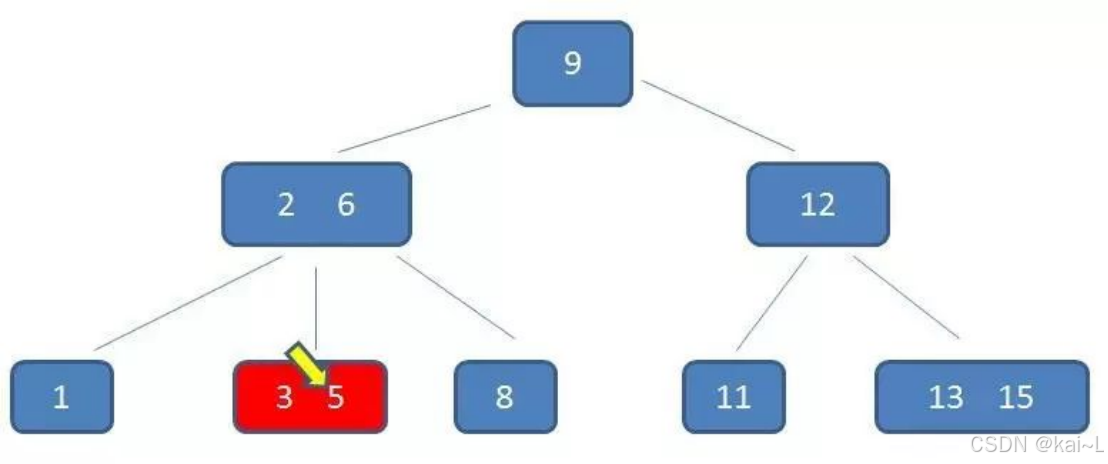
可以看出b-树在查询时比较次数不比二叉查找树少，相比磁盘io的速度，内存中的耗时可以忽略不计，节点下内部元素只要不超过磁盘页的大小，无非多几次内存交互。