二叉树的存储结构与递归遍历方式

二叉树可以看成是一个有穷结点的集合，由根节点和其互不相交的左子树和右子树组成，所以二叉树的度等于2。（但是注意不是所有度为2的树都是二叉树。）

二叉树有斜二叉树：

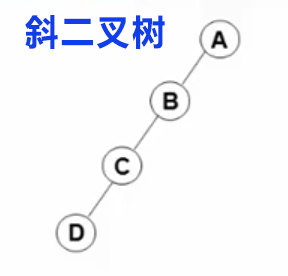
也就是只有左子树或者右子树，它的另一个指针域为空，这样的二叉树其实就是一个链表。

如果既有左子树又有右子树，像这样的情况，成为完美二叉树：

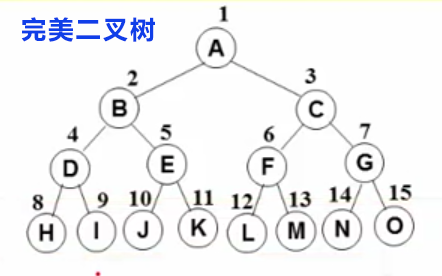
也就是除了叶结点外，每一个结点都有左子树和右子树，叶节点是比较齐的，处于同一层。

对于二叉树的操作，这里讲一些最基本的操作有：

1、创建一个二叉树；

2、判断二叉树是否为空；

3、遍历二叉树；

其中第三点遍历二叉树十分重要，因为在树的操作中，很多时候都要遍历访问数据。至于树的遍历方式在这里先讲三种递归的方式：

1、先序遍历：依次按根、左子树、右子树的顺序遍历。

2、中序遍历：依次按左子树、根、右子树的顺序遍历。

3、后序遍历：依次按左子树、右子树、根的顺序遍历。

接下来先看二叉树的存储方式后，再来实现二叉树的遍历。一般的二叉树可以用这样的结构来表示：

一共三个域，一个Data表示信息，一个Left结构指针和一个Right结构指针表示左子树结点和右子树结点。

存储完后接下来到遍历，首先来看先序遍历，先序遍历的过程是先访问根结点，接着按照先序遍历的原则遍历根节点之后的左子树，再遍历右子树，这样遍历可以用递归的方式。因为按照先序遍历的原则（先访问根节点，接着遍历左子树再遍历右子树），我们可以用递归的方式，递归的遍历左子树后，再递归的遍历右子树。

所以递归的代码可以写成这样：

函数中传进去一个树BT，在第37行if先判断树是不是空的，不空的话就先访问根节点（第38行），这里的访问方式也就是把它输出来看一下。接着就递归遍历左子树，递归完左子树后再递归右子树。

所以按照这种方法，我们用个例子来看下先序遍历是怎么进行的：

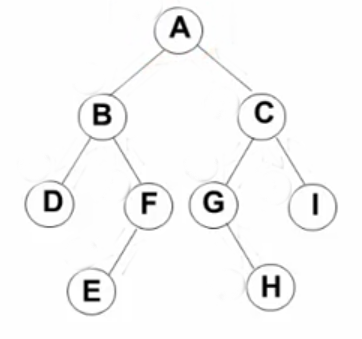
一开始进入A根节点，判断不空后，就输出A的Data，然后对左子树递归，也就是对B子树以下的进行遍历，遍历B的方法因为同样是递归，判断B不空后，输出B，然后对左子树遍历，再对右子树遍历，所以输出的顺序是ABD，输出完D后，B的左边遍历完了，接着遍历B的右边，B的右边同样的方法先根节点然后从左到右，所以A的整个左边遍历顺序是ABDFE。

然后对A的右边遍历，方法一样，所以最后遍历的顺序是CGHI。这个例子整个遍历顺序就是左+右得ABDFECGHI。

接着到中序遍历：中序遍历是按左子树、根、右子树的顺序遍历，所以显而易见只要把访问根的语句放到递归左子树之后就可以了。

同样那回上面那个例子图：

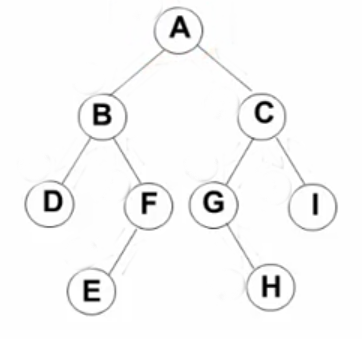
显然，左边的遍历顺序是DBEF，遍历完左边后，就访问根节点A，接着才到右边的遍历，右边的遍历按照同样的方法，所以遍历顺序是GHCI，整个遍历顺序就是DBEFAGHCI。

最后到后序遍历：后序遍历一样，依次按左子树、右子树、根的顺序遍历。所以把访问根节点的语句放到最后，也就是放到遍历右结点的语句之后。

回到上面的例子图，后序遍历，先把左子树遍历完后，接着遍历右子树，最后再访问根节点A，最后整个遍历顺序就是DEFBHGICA。