力封闭抓取笼的构建与检测

笼与力封闭抓取之间的关系

相关工作

在机器人抓取领域，许多研究工作聚焦于基于特定条件（如力闭合或围捕）的抓取计算，以防止被抓取物体发生运动。已有研究对力闭合或形闭合抓取领域进行了综述[1]。与以往需要精确位姿估计的精密操作研究不同，围捕方法使我们能够应对物体的位姿不确定性。实用笼形结构的研究对于实现单自由度工业夹爪的抓取机制具有重要意义。本文首先回顾针对二维（2‐D）或三维（3‐D）物体的围捕抓取相关工作，随后介绍本研究的目标。

围捕问题最初由库珀伯格提出，其中围捕被定义为一组销钉以某种方式放置，从而阻止多边形从给定位置[2]进行任意运动。自那以后，各种围捕

这些条件已被研究并应用于抓取问题。克里格曼等人将围捕定义为一组系统构型，这些构型可能无法完全固定被操作的物体，但能防止该物体逃逸到无穷远处[3]。

使用双销夹持器进行围捕

双销夹持器是合适的ble f 或围捕凹形物体。苏桑和皮帕塔纳松提出了一种组合算法，通过识别相关的代表性销钉放置位置和临界距离[4]，来报告两销及给定平面多边形凹面的所有围捕集合。里蒙等人提出了单参数双销夹持器的围捕抓取方法，其中围捕集合被定义为保持物体被围栏或限制在销钉之间的手部构型[5]。戈帕拉克里希南和戈德堡讨论了双销夹持器对多边形和多面体部件的外部或内部凹面进行接触时的围捕抓取[6]。当两销形成V型夹持（即销钉放置在这些顶点上可实现力闭合）后，它们可以在保持围捕条件的同时移动、挤压或拉伸一定距离。牧田等人提出了两种围捕类型：环型和腰型围笼，这两种类型均可通过双销夹持器实现[7]。

使用三销或多销夹持器进行围捕

The devel发展o f围捕能力 bil 使用具有三个或更多销钉的夹持器进行围捕非常重要，因为双销夹持器无法对凸形物体实现围捕。大卫森等人分析了使用三指夹持器对二维多边形物体进行围困的问题，其中物体通过销钉被完全固定在固定抓取中[8]，并且他们还将该围捕方法扩展到了基于视觉的抓取[9]。埃里克森等人研究了使用三个销钉围困凸多边形物体的问题；他们提出了精确和近似算法来生成围困区域，假设所有销钉都固定在凸形物体的边界上[10]。罗德里格斯等人讨论了刚性二维物体在使用两个或三个销钉时抓取与笼形结构之间的关系。他们说明了一些笼形结构特别适合作为抓取物体的路径点，即存在一组机械手的构型，使得物体不会脱离机械手的可及范围[11]。

瓦赫迪和范德斯塔彭开发了使用三个销钉围捕多边形物体的算法。他们在已知两个基销放置位置的情况下，计算了第三个销钉所有可能的放置位置[12]。迪安科夫等人通过计算针对特定物体的围捕抓取，报告了多销夹持器的抓取规划。他们将笼定义为机器人手爪将物体的构型空间限制在有限体积内的状态[13]。万等人实施了一种围困式抓取方法。他们证明了最小围困即为固定不动[14]。佩雷拉等人提出了通过围捕利用多个移动机器人操纵物体的算法。他们定义了确保物体在过程中被围栏的条件

操作[15]。扎鲁宾等人通过在物体表面使用测地球来近似夹持器与物体之间的最大接触表面，利用真实夹持器仿真生成围捕抓取[16]。福井设计了一种专门用于二维形状围困操作的末端执行器[17]。贾等人将围困策略扩展到可变形环状二维物体的挤压[18]。

本工作目的

通常情况下，并非所有笼形结构都适用于实现力封闭抓取。所谓力封闭抓取的笼形结构，是指存在一组夹持器构型，使得物体无法逃脱，并在夹持器达到作用范围时最终形成力闭合。然而，已有若干研究针对力封闭抓取的笼形结构问题展开，且大多数先前的围捕策略主要集中于平面物体上。

本研究的主要贡献是提出一种用于抓取二维多边形和三维多面体物体的力封闭抓取笼。我们参考了近期算法中提出的抓取笼[11]和通过围捕抓取[14]的概念。然而，我们的工作与他们的研究存在一些差异：1）抓取笼并不一定意味着完全固定，即它不一定是力封闭抓取（力封闭抓取是指完全固定）；2）通过围捕抓取的最终状态是一种平衡抓取。而力封闭抓取笼是一种力封闭抓取。需要注意的是，力闭合意味着平衡，但也存在一些力/力矩系统能够实现平衡但未达到力闭合[1]。

为了实现对三维物体的围捕抓取，我们通常需要在六维（6‐D）构型空间中识别所有的围捕集合，这在计算上非常昂贵。本文将高维围捕问题分解为两个子问题：在一个子空间中，我们寻找笼形结构以确保物体不会脱离销钉的范围；然后，在另一个子空间中，我们规划一条路径，引导物体收敛到吸引区域的最小值。

定义与符号

在本节中，我们介绍一些与吸引区域、笼形结构、力闭合以及力封闭抓取笼相关的概念和定义。夹持器构型涉及销钉在夹持器构型空间中的放置。当销钉与物体表面接触且满足抓取准则时，该夹持器构型被定义为抓取构型[1]。若物体无法从某一夹持器构型中逃逸，只要保持销钉位于该集合内，则称此构型为笼形结构。

当不存在任何平移和旋转的序列能使物体脱离由夹持器销钉[14]构成的障碍物时，称该夹持器对多面体物体实现了笼形抓取。

围捕抓取能够保证当销钉移动到目标位置时，物体随之一起移动。围捕抓取的集合远大于形封闭抓取的集合。此外，围捕抓取要简单得多

对指尖放置位置的误差不敏感。解除围栏抓取无法确保在执行抓取动作时物体始终被夹持器包围。力闭合与约束装置仅依靠单面无摩擦接触约束[1]来限制被抓取物体运动的能力相关。力闭合是一种完全约束状态，在此状态下，被抓取物体能够抵抗任意外部扰动力矩，而无需依赖接触力的大小。力封闭抓取笼定义为一种笼形结构，其中夹持器在构型空间中的一组构型将围捕构型转变为力闭合构型。

我们使用术语initial-grasping cage来指代能够产生通往物体抓取的受限路径的笼形结构，并将力封闭抓取笼作为我们期望达到力闭合抓取的一种抓取类型。

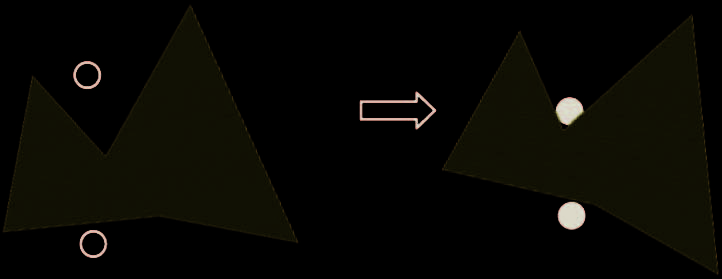
图1(a)展示了一个力封闭抓取笼。由两个空心圆所示的初始抓取构型构成一个笼，因为它限制了物体的可移动性。两个实心圆实现了力闭合抓取，因为它们限制了物体的所有运动。我们认为该笼形结构是一个力封闭抓取笼，因为它能够实现力闭合抓取。

图1(b)展示了一种围栏抓取，但不具备力闭合。由两个空心圆所示的初始抓取构型是一个笼形结构。尽管两个实心圆也形成了一个笼形结构，但它们不构成力封闭抓取，因为无法限制物体的所有运动。更重要的是，该笼形结构比力封闭抓取笼的集合更大。然而需要注意的是，笼形结构不足以实现物体的完全固定。还需注意，力封闭抓取笼足以实现物体的完全固定，并且它始终是一种笼形结构。

吸引区域[19]被定义为一组抓取构型，从这些构型出发，在主动作用力下物体会被抓取至稳定状态。我们假设存在一个非线性系统dX/dt= f(X,F,t)，其中X是物体状态且F表示夹持器对物体的夹持力。对于区域X中的所有X，如果存在一个状态无关输入F和一个特殊函数g(X)满足：

(C1)() () , g X g X X X when 0 0 2 !

() () , g X g X X X when 0 0 = =

(C2)g (X)对X的所有分量具有连续偏导数

(C3) () d d g X t 10.

然后，物体状态在区域Ω内是稳定的，该区域被称为吸引区域，函数g被称为吸引函数。接下来，我们将讨论一种基于吸引区域确定力封闭抓取笼的算法。

检测力封闭抓取笼

吸引区域中的笼通常是一种力封闭抓取笼，因为它会收敛到该区域的最小值。为了实现力封闭抓取笼，我们可以在构型空间中构建吸引区域。

形态闭合抓取笼的条件

根据定义，一个吸引区域： ●是一个光滑的碗形区域 ●具有一个V形底部，该底部表示区域的最小值，并表明存在力封闭抓取 ●由一条闭合曲线包围。

注意，吸引区域上的一个点表示一种抓取构型，即对应于销钉的某些放置位置以及被抓取物体的某一状态。还需注意，光滑的碗形表面意味着该表面关于所有分量具有连续偏导数。

图2(a)和(b)展示了在构型空间中形成的两个吸引区域。箭头表示点的可能运动方向。注意，状态ss1 4以及靠近s3的状态都会收敛到。s3此外，由于只有一个特定的抓取构型与，s3相对应，我们认为物体的所有运动都完全受限。在这种情况下，我们将s3称为该区域的V形底部。

注意，碗状区域可能具有平底，如图2(c)所示。还请注意，平底并不意味着力封闭抓取。例如，状态s5能够转移到,s6，即与平底相关的抓取构型不稳定。

在图2(d)和(e)中，我们讨论了两个非吸引区域的例子，其中(d)表示一个半碗形，(e)表示两个子碗形。在图2(d)中，状态s7和s9属于半碗形，但当s8满足g(X)= 0时，不是可行的抓取候选。因此，状态s7不是一个笼，因为它可能转移到。s8在图2(e)中，状态s10位于左子碗内，状态s11位于右子碗内；状态s12位于

曲线的交点。状态s12可以转移到s10或,s11因此该区域不是吸引区域。

检测吸引区域

我们提出了一种算法来确定吸引区域，该算法有助于生成一组力封闭抓取笼。表1定义了本节中使用的重要符号。设c(X)= σ为用平面g(X)= σ切割曲面g(X)时得到的曲线。我们假设

() S X g X# v = v” , (1)

and

() () | U X g X X !S = v ” ,. (2)

算法1描述了吸引区域的检测过程。需要注意的是，具有V形底部并由闭合曲线包围的碗形区域即为吸引区域。闭合曲线是一个连续的环路，且不与自身相交。

在接下来的部分中，该闭合曲线由区域的边界定义。

使用双销夹持器的围栏抓取

我们描述了使用两指夹持器对平面零件进行围捕。图3显示了夹持器坐标系。物体中心由其几何中心定义。我们通过一个特殊函数来定义

() | |, | | max c o c o g X ,, x y g g 1 2 z = i ^ h. (3)

检测力封闭抓取笼

我们使用一个具有五个顶点的凹多边形作为示例，来描述力封闭抓取的检测。

算法1

输入：g(X)的曲面。

步骤1：检测g(X)的一个局部最小值，记为g(X0)。如果无法找到g(X0)，则跳转至退出。

步骤2：初始化gX0 3v v= + ^ h

步骤3：使用平面,Xgv= ^ h对g(X)的曲面进行切片，并获得曲线.cXv= ^ h

步骤4：如果c(X)是闭合的，则使用(2)计算U(X)。然后更新v并转到步骤3。

步骤5：否则如果不存在闭合曲线，则转到退出；否则转到输出。

输出：U(X)是一个吸引区域。

退出：U(X)不是一个吸引区域。

(a) (b)

(c)

(d) (e)

s1 s1

s2 s2

s4 s4

s3 s3

s5 s6

s7 s8

s9

s10 s11

s12

图2. (a)和(b)状态s1显示一个力封闭抓取笼。无论是否转移到s2或,s4，抓取构型仍处于碗形区域内，并最终转移到状态s3和(c)该区域的平底。(d)状态s7显示非笼状构型，仿佛可能转移到某个随机状态，例如状态,s8以及(e)状态s12显示一个笼，但不是力封闭抓取笼，因为它可能转移到s10或.s11

表1. 检测吸引区域时使用的符号。

符号	定义
g(X)	吸引函数
U(X)	吸引区域
U(X0)	U的最小值
X	物体的状态
X0	物体的状态获取 U的最小值
Xg	抓取构型
v	一个实数
Sv	物体状态的集合
吸引区域U(X)
c(X)	通过切割曲面形成的曲线 g(X)的表面
xg og yg	夹持器参考坐标系
og	两个销钉的中心
(x,y)	物体中心的位置在 xg og yg坐标系上
iz	物体的旋转角 绕z轴
ci(i= 1,2)	多边形的交点 与yg轴
|ci og| (i= 1, 2)	ci和og之间的距离

凹多边形的五条边Ek(k= 1,…,5)如图4(a)所示，可表示如下：

, y y y y x x x x k k l k k k l k 1 1 = + + ----(4)

其中,y y 0 k +1 k!-x x 0 k +1 k!-(k= 1,…,5)，,x yl l^ h是边上的一个点，而,x yk k^ h（k= 1,2,3,4,5）是多边形顶点的位置。

请注意，,x yk k^ h的位置将随着由抓取动作引起的物体的旋转（由zi描述）和运动（由x和y描述）而发生变化。因此，与y轴的交点,y 0 f i ^ h（i= 1,2）满足

, ,. y y y y x x x i 1 2 k k f k k k k 1 1 i = = + + ----(5)

假设多边形绕z轴（垂直于x oyg g g平面的轴）旋转，或在施加挤压作用力时沿x oyg g g平面平移。我们用,xyk kl l ^ h表示运动和旋转后点,xyk k^ h在x oyg g g平面上的坐标，并用(x, y)表示多边形中心,ot的位置。我们得到

. cos sin sin cos x y x y x y 1 0 0 1 1 k k k k z 0 0 z z z $ i i i i = - l l R T SSSS > > V X WWWW H H (6)

由(4)–(6)可得抓取多边形的函数。

( ) ( ) ( ) ( ) ( ), y x y y x y x x x y y x x y y s c c s c s s c , , , , f z k z k z k z k z k k z k k z k k z k k 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 i $ i i i i i i i i = + +–+ ----+ - + + + + (7)

引脚‐2

引脚‐ 1

xg

yg

c1

c2 og

(b) (a)

xg yg

og

图3. (a)夹持器坐标系，其中 og为两销中心，yg轴穿过两销，xg轴垂直于yg轴；(b)物体和两销在x oyg g g平面上的投影。

(x1,y1) (x4,y4)

(x2,y2) (x3,y3)

(x5,y5) ot

o g

yg

x g θz

(a) (b)

c2

c1

20 15 10 5 0 3 2.8 2.6 2.4 2.2 2 0.5 0

a2 a1

y/cm

/c m

x/cm

θ/rad

( )/c m

–0.5

14 12 10 8 6 4 2 0 –2 –4 –10 –5 0 5 10

/c m

x/cm (c) (d)

14 12 10 8 6 4 2 0 –2 –4 –10 –5 0 5 10

引脚‐ 1

引脚‐ 1

引脚‐ 2 引脚‐ 2

图4. (a)被抓取的凹多边形，(b)吸引区域，其中红色曲线为边界，(c)力封闭抓取笼对应于点,a1以及(d)力封闭抓取对应于最小值点.a2

其中，i，sins 2 = f> < f 1 ii，，cosyy00 czzzzi=且，xy k0 0 ^ h和，xy , , 1 0 1 0 + + ^ k kh分别是顶点，xykk^ h和，，xy k 1 1 + + ^ kh的初始位置。

因此，g(X)的图像（其中我们假设x= 0在(3)中）可如图4(b)所示获得。在图4(c)和(d)中，我们展示了初始的抓取笼形结构和最终的力封闭抓取。注意，由红色曲线围成的碗形区域是一个吸引区域，其中红色曲线是吸引区域的边界。还要注意，点a2是吸引区域的最小值，而点a1是吸引区域上的一个点；因此，它表示一个力闭合抓取笼形结构。与点Xg相关的抓取构型a1和a2分别如图4(c)和(d)所示。

使用双销夹持器对杆进行围捕的仿真与实验

我们考虑ductt he模拟lationan d practica l使用双销夹持器进行实验。首先，我们利用ADAMS软件工具（MSC软件公司的动力学仿真软件）对围捕过程进行仿真，从而分析抓取过程中被夹持部件与夹持器销钉之间的运动和力。

我们首先建立吸引区域，如图5(a)所示。注意，由两条红色曲线包围的两个碗形区域即为两个吸引区域，这两条红色曲线是两个吸引区域的边界。还请注意，点a2是吸引区域的最小值

区域。点a1是吸引区域上的一点，因此它表示一个力封闭抓取笼。与点a1和a2相关的抓取构型分别如图5(b)和(c)所示。图5(c)展示了一个力闭合抓取。一旦我们获得了力封闭抓取笼，就可以执行抓取，如图6和图7所示。

20 10 0 –0.5 0 0.5 –2.5 –2 –1.5 –0.5 –1 y/cm x/cm x/cm (b) (a) (c) /c m θ/rad ( )/ cm 4 2 0 –2 –4 –6 –8 –10 –12 –10 –5 0 5 10 /c m 4 2 0 –2 –4 –6 –8 –10 –12 吸引区域 a1 a2 引脚‐ 1 引脚‐ 1 引脚‐ 2 引脚‐ 2

图5。(a)红色曲线描绘了吸引区域的边界，(b)力封闭抓取笼对应于点,a1，以及(c)力封闭抓取对应于最小值点.a2

(a) (b) (c) (d)

图6。(a)夹持器接近杆，(b)力封闭抓取笼，(c)挤压过程中物体在内部旋转和移动，以及(d)力封闭抓取笼最终实现力封闭抓取。

使用三指夹持器对平面零件的围捕

在本节中，我们描述了使用三指夹持器对杆进行围捕的过程，其销钉同时挤压并停止。我们在夹持器上建立了一个参考坐标系，如图8所示，其中xoyggg是建立在夹持器上的坐标系，go是三个销钉的中心，且gy轴通过引脚‐3和go。x轴垂直于yg轴。注意，直线（go,引脚‐1）与直线（go,引脚‐2），以及直线（go,引脚‐2）与直线（go,引脚‐3）之间的角度均为2π/3。

我们用,,Xxy zi=^ h表示物体在ggxoyg坐标系中的物体的状态，其中zi是物体绕垂直于xoyggg平面的轴的旋转角，(x,y)表示物体中心的位置。我们定义一个特殊函数为

| |, | |, | | () , max c c c g X ,, g g g x y 1 2 3 z = i o o o ^ h (8)

其中ci(i= 1,2,3)是边与通过og和引脚i的直线的交点，coig(i= 1, 2, 3)是点ci与og之间的距离。

(a) (b) (c) (d)

图7。(a)夹持器移动到围捕配置时的状态，以及(b)物体被牢固抓取之后的状态。

引脚‐ 2

引脚‐3

引脚‐ 1

x g

y g

c 1 c 2

c 3

o g

x g

y g

o g

(b) (a)

图8。(a)三指夹持器的坐标系和(b)物体及销钉在x o y g g g平面上的位置。

笼与力封闭抓取之间的关系

形态闭合抓取笼的检测

我们使用一个具有四个顶点的凸多边形，如图9(a)所示，来描述力封闭抓取笼的检测。吸引函数的构建与双销夹持器的情况类似。

交点,xyf i f i^ h(i= 1,2,3)满足

f , arctan ; arctan , f y y y y x x x x y x y x x y 5 6 6 0 0 k f k k f f f 1 1 1 i i k k k f f 1 3 2 2 3 1 r r –=– = = = + + ^ ^ h h Z [ \ ] ] ]] (9)

其中,y y 0 k +1 k!-x x 0 k +1 k!-(k= 1,…,4)，且,x yk k^ h是多边形顶点的初始位置。

边的状态应随物体的位姿（x、y和zi坐标）而变化，这导致了。ci因此，我们得到了g（X）的图像，如图9(b)所示。在图9(c)和(d)中，我们展示了力封闭抓取笼和最终的力封闭抓取。注意，由红色曲线围成的碗形区域是一个吸引区域，其中红色曲线是吸引区域的开口。

使用三指夹持器对杆状物体进行围捕的仿真与实验

我们使用三指夹持器进行了仿真和实际实验。函数g的图像如图10所示。红色曲线是吸引区域的边界，可通过算法1获得。点a2位于中间吸引区域内，因此适用于力封闭抓取笼形结构。点a1是吸引区域的最小值，因此对应于一个力闭合抓取。这两个点对应的抓取构型分别如图10(b)和(c)所示。

首先，我们使用软件ADAMS模拟围捕过程，如图11(a)–(c)所示。用于围捕抓取的实际实验如图12(a)和(b)所示。注意，初始围捕构型，即三个销钉的初始位置，来自图10(b)。

(a) (b) (c) (d)

图9.(a)吸引的区域，其边界用红线表示，(b)该点的力封闭抓取笼a1,(c)力闭合的抓持sp表示最小值点,a2以及(d)力封闭抓取。

20 30 40 10 0 0.5 0 –0.5 0.2 0.1 0 –0.1 –0.2 y/cm x/cm x/cm (b) (a) (c) /c m θ/弧度 ( )/c m 6 4 2 0 –2 –4 –6 –4–202 4 6 81012 /c m 6 4 2 0 –2 –4 –6 –4–202 4 6 81012 /rad 引脚‐ 1 引脚‐ 1 引脚‐ 2 引脚‐ 2 引脚‐ 3 引脚‐ 3 a1 a2 吸引的 区域

图10.(a)在与,,ygz i^ h相关的子空间中形成的吸引区域；红色曲线是吸引区域的边界，(b)对应于吸引区域点a1的力封闭抓取笼，以及(c)对应于吸引区域最小值点a2的力封闭抓取。

(a) (b) (c) (d)

图11.(a)夹持器接近杆的过程，(b)力封闭抓取笼，(c)笼形结构最终实现力封闭抓取，以及(d)杆被拾取后的状态。

(a) (b)

图12.(a)夹持器在移动到笼型配置时的状态，以及(b)物体被牢固抓取后的状态。

使用三指夹持器围捕三维物体

As discusse d在前面的章节中，t h围捕o f pl anar部件主要涉及二维运动（即在xoyggg平面内的平移和绕zg轴的旋转）。然而，在对多面体进行围捕时，物体在三维空间中的俯仰或滚动旋转可能会改变期望的围捕构型。表2定义了本节中使用的重要符号。

夹持器坐标系的定义如图13所示。

我们通过定义一个特殊函数

() | |, | |, | | . max c c c g X ,,,, g g g x y 1 2 3 x y z = i i i o o o ^ h (10)

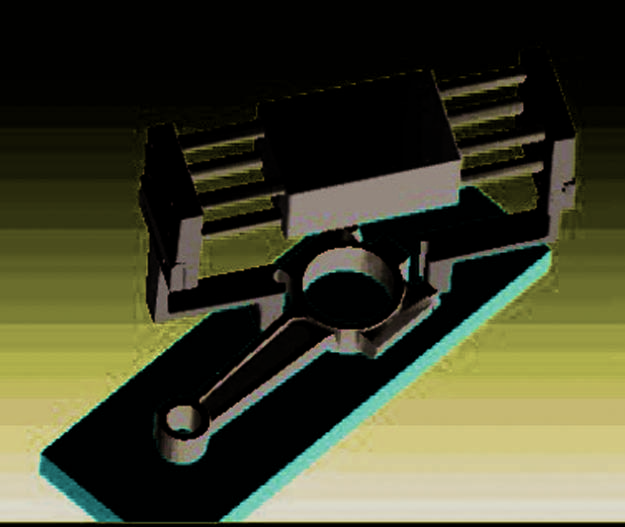
引脚‐ 1 引脚‐2 引脚‐ 3 x y z g x g y g o g (b) (a) θx θy c1 c2 c3 o 图13.(a)三指夹持器的坐标系，其中 yg轴穿过夹持器中心og和引脚‐3，且zg轴垂直于夹持器的掌面。(b)物体和销钉在x oyg g g平面上的投影，其中 x轴与xg轴平行，y轴与yg轴平行，且o是. og的投影

表2. 使用三指夹持器围捕三维物体讨论中使用的符号。

符号	定义
xg yg o点g zg	夹持器参考坐标系
o g	夹爪底平面的中心
o	在支撑平面上的投影
xoy	支撑平面
X	物体的状态
(x,y, z)	物体中心的位置在 the x g yg og zg 坐标系
(ix,iy,iz)	多面体的旋转角 分别围绕xg、yg和zg轴
ci	边与交点 穿过og和夹爪i的直线
|ciog |	ci与o之间的距离 g g1 对应的次吸引函数 到(x, y , i z)
g2	对应的次吸引函数 到(i x , i y )
di 1	次吸引函数g1的最小值 under , x xi ii = y = yi ii

由于 X定义在六维空间中，通常很难在高维空间中搜索笼。我们可以通过将高维问题转化为一组低维问题来解决此问题。我们提出了一种方法，将由吸引函数描述的高维构型空间分解为两个子函数。

在子空间(,,,)xy gz 1i中，我们定义

| |, | |, | | . max c c c g ,, g g g x y 1 1 2 3 z = i o o o ^ h (11)

注意，g1的定义与(3)中的定义类似。还应注意，g1由物体的投影决定。在子空间(,,),gxy 2ii中，我们定义

{} g d (,) i 2 1 x y 2 = ! i i X, (12)

其中

1(,,) min g d x y ,, , i x y z 1 z x x i y y i i = i i i i i == ^ h . (13)

在低维子空间中检测笼如(10)–(12)所述，我们首先通过设置(,,, gxy z 1 = ) y x y = ) i在子空间中建立吸引函数(,xii)ii。然后，我们利用子空间(),,,gx y 2ii中的吸引函数的最小值，在子空间(,,),gxy z 1i中构造吸引函数。算法2展示了两个子函数(,,)xyg z 1 i和(,)g x y 2i i的计算。

被抓取的多面体状物体及其凸包如图14(a)所示。我们构建了吸引力函数，g2的图，如图14(b)所示。图14(c)中由虚线标记的子区域在图15和图16中被突出显示。

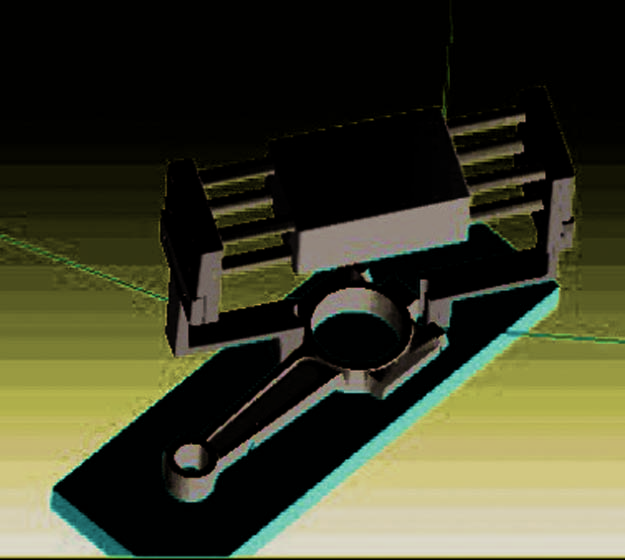
算法2

输入：多面体的顶点

步骤1: 设置x xii= ), y yii= )，并将物体投影到xoy平面。

步骤2: 使用构造子函数g1 | | , | | , | | max c o c o c o g ,, x y U g gg 1 1 2 3 z 1 = i! ^ h

步骤3: 在子空间(,,,)x y gz 1i中找到吸引区域，并使用计算吸引函数的最小值 1(,,) min g d x y ,, i x y z 1 z i = i ^ h

步骤6: 改变方向(,)x y 2!iiX物体的方向，然后返回步骤2。

步骤5: 使用构造吸引子函数g2 {} g di 2 =1

步骤6: 在子空间(,,)gx y 2ii中使用表1中提出的算法找到吸引区域。

输出：一组力封闭抓取笼

4.3 4.2 4.1 4 3.9 3.8 0.5 0 –0.5 –0.5 0 0.5 2 θ y θ x 7 6 5 4 3 1 1 0.5 0.5 0 0 –0.5 –0.5 –1 –1 –2 –1 0 1 2 1 /c m 7 6 5 4 3 1 /c m θ/rad θ/rad y/cm –2 –1 0 1 2 y/cm (c) (b) (a) (d) (e) C D B A 4 3 2 1 –1 –2 –3 –4 0 x/厘米 /c m 引脚‐ 1 引脚‐ 2 引脚‐ 3 4 5 3 2 1 –1 –2 –3 –4 0 x/厘米 /c m 引脚‐ 1 引脚‐ 2 引脚‐ 3

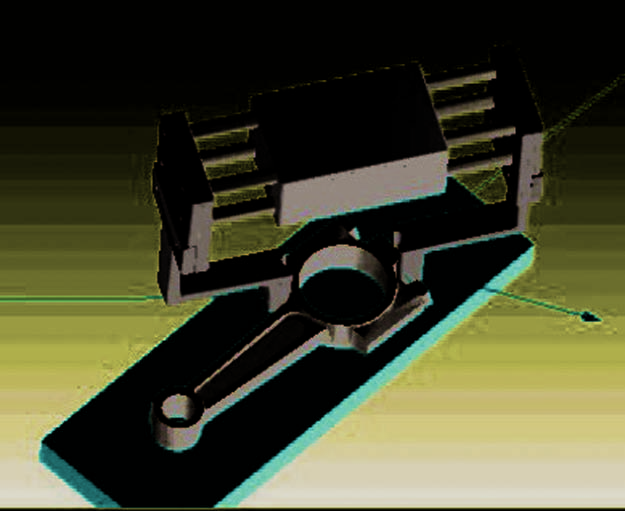
图15。(a)吸引区域形成于与,,,gx y 2 i i^ h相关的子空间中；(b)在子空间,,y g z 1 i^ h中的图形与A相关，其中C表示笼型配置(c)；(c)和(d)在子空间,,y g z 1 i^ h中形成的图形与B相关，其中D对应于力封闭抓取(e)。

4 3 2 1 2 4 2 0 –2 –4–4 –2 0 2 4 3 4 5 6 4 2 0 0 2 4 6 x θx θy y 2 (a) (b) (c)

图16 图15

图14.(a)被抓取物体和(b)与(c)吸引函数的图像.g2

图15(a)显示了与(,,)gx y 2ii相关的子空间中的碗形吸引区域。g1的吸引函数图像，当.,., 0 075 0 085 x y ii = = ^ h时，它对应于构型B的.g2图15(c)是吸引函数g1 的图形在,, 0 0 x== ^ yiih时对应于构型A的.g2 。注意，构型A是与(,,)gxy 2ii相关子空间中吸引区域的最小值。图15(c)所示的围捕配置对应于 g1 在.,.. 0 075 0 085 x yii= = ^ h时的 构型C。图15(e)所示的围捕配置对应于g1 在,. 0 0 x== ^ yiih时的构型D。注意，在图15(e)中，投影多边形被三个销钉牢固地约束。

图16(a)显示了与(,,)gx y 2ii相关的子空间中的一个非吸引区域。图16(b)是当.,., 1 5 1 5 x= y ii-= ^ h时吸引函数g1的图像，它对应于.g2的构型 E。图16(c)所示的抓取构型对应于当.,.. 1 5 1 5 x = y i i-= ^ h时g1的构型F。注意，在图16(c)中，物体能够从三个销钉的间隙中逃脱，例如，沿红色箭头标记的方向为逃了脱确。定计算复杂度，我们在一台配备3.6吉赫中央处理器和4.0GB随机存取内存的个人计算机上使用MATLAB进行仿真，围捕物体的三指夹持器计算累积运行时间列于表3。搜索空间由30x数据（沿x轴的运动）、30 xi数据（绕x轴的旋转角度）、30 yi数据（绕y轴的旋转角度）以及30 zi数据（旋转角度）组合而成位于z轴上方）。该算法的搜索空间由多面体物体位姿的区间离散数据以及物体的顶点数量决定。由于搜索空间通常小得多，因此该算法在围捕具有较少顶点的平面或三维物体时应运行得较快。

表3. 算法的性能。

数量 顶点	时间（秒）
杆[图8(b)]	17
多面体	8
螺栓[图14(a)]	24
多面体	781

使用三指夹持器对三维物体进行围捕或解除包围的仿真与实验

我们进行两个涉及的实验 d实现围栏抓取 d 一种解除围栏抓取。

围栏抓取

我们假如设图1t5 h(c)所示的初始围捕构型。然后我们使用该构型进行围捕过程的仿真ADAMS，如图17(a)–(d)所示。使用三指夹持器的实际实验如图18(a)–(b)所示。

解除围栏抓取

我们假设t h 初始的解除包围构型如图16(c)所示。然后我们使用ADAMS对整个围栏抓取过程进行仿真，如图1 9(a)–(d)所示。实际的抓取实验在图20(a)–(b)中进行了演示。

结论

本研究探讨了笼与单自由度两指或三指夹持器的力封闭抓取（完全固定）之间的关系。因此，被围栏的物体最终将到达一个稳定状态，这对于夹持器的工业应用具有实际意义。

基于夹持器约束形成的吸引区域来检测力闭合抓取笼的方法如下：我们首先在构型空间中构造一个特殊函数，并将其称为吸引函数。然后，我们检测该吸引函数的最小值及其边界。吸引函数的最小值表示一个力封闭抓取，吸引函数的边界则包围了吸引区域上的笼形集合。

因此，我们可以选择一个初始的围栏抓取，最终在吸引区域上实现力封闭抓取。对于三维物体的围捕，我们将高维构型空间中的吸引函数分解为低维子空间中的两个子函数。所提出的方法可用于使用单自由度工业夹爪对类多边形或类多面体物体进行抓取。

夹持器形成的吸引区域用于消除夹持器的不确定性，并实现稳定的抓取。在其他操作系统构型空间中，也可以获得类似的约束区域。我们可以根据不同应用的环境约束，在构型空间中构建所需的吸引区域，例如销孔插入或物体的无传感器定位。我们目前的研究包括使用工业夹持器对已知工件进行围捕，其中夹持器仅有1或2个自由度。在未来的工作中，我们将讨论对未知物体的围捕。在这种情况下，视觉不仅应用于识别物体的初始位姿，还应引导抓取动作。