【没事儿看两道Leetcode系列】100热题之数组

数组

53. 最大子数组和

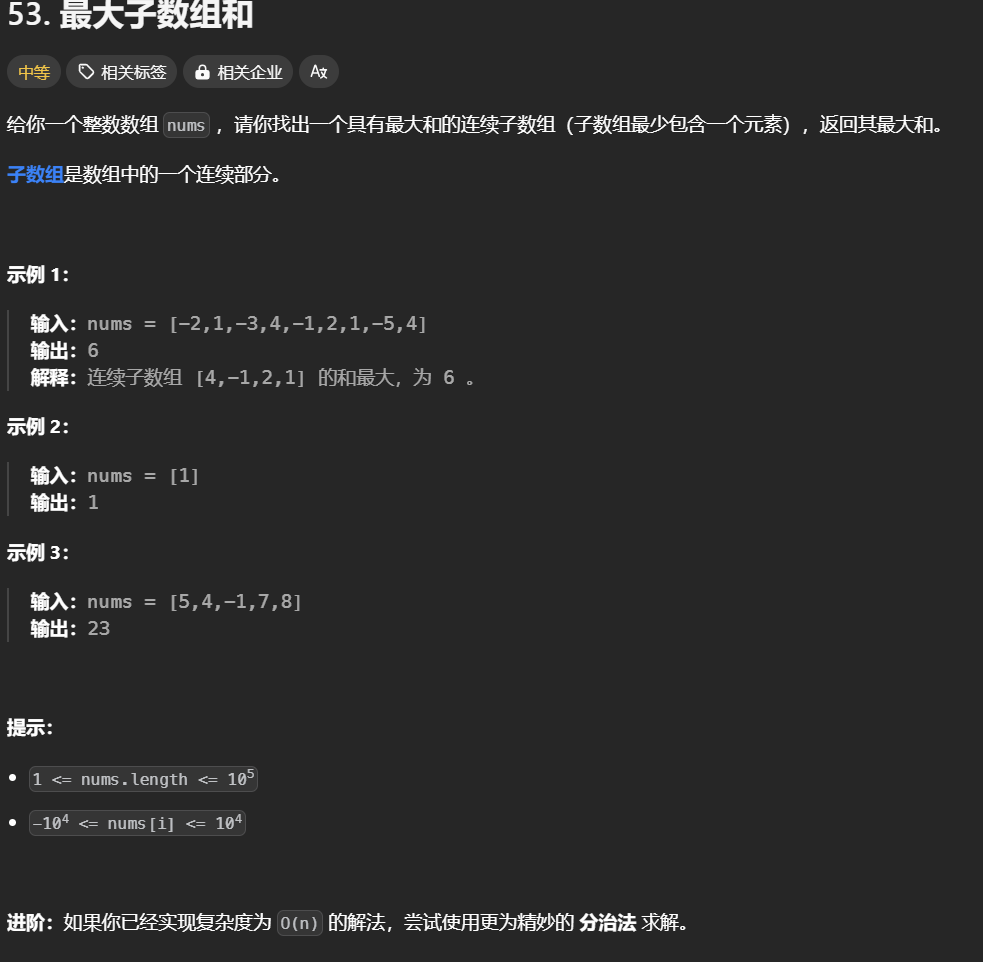
普通做法：O(n^2) 双层循环，找到所有可能的子数组和其求和，依次与最大数组求和比较是否更新。

我选择动态规划做法，不研究分治了，贪心也不错而且写起来还简单。

简单来说就是从数组开头开始依次加每个元素，如果当前数组和为负数就可以把这部分数组和全部舍弃掉，从0开始累加下一个数组元素。因为左侧部分如果求和是负数，那么加到右侧部分只可能会让右侧的数组总和变得更小，只有舍弃掉负数部分才能取到最大值。

还有一种额外情况是形如：[-1] 这样的数组。数组中只有一个元素而且是负数，最大和就是-1而不是0，所以我们找不到比0大的数组最大和。所以我们可以设定初始数组值为一个非常小的负数，先判断当前数组和是否大于最大值，再判断当前数组和是否小于零，小于零舍弃，继续遍历。

class Solution {
    public int maxSubArray(int[] nums) {
        int sum = 0, pre = 0, temp_sum = 0, max_sum = -10000;
        for (int i = 0; i < nums.length; i++) {
            temp_sum += nums[i];
            if (max_sum < temp_sum)
                max_sum = temp_sum;
            if (temp_sum < 0)
                temp_sum = 0;
        }
        return max_sum;
    }
}

56. 合并区间

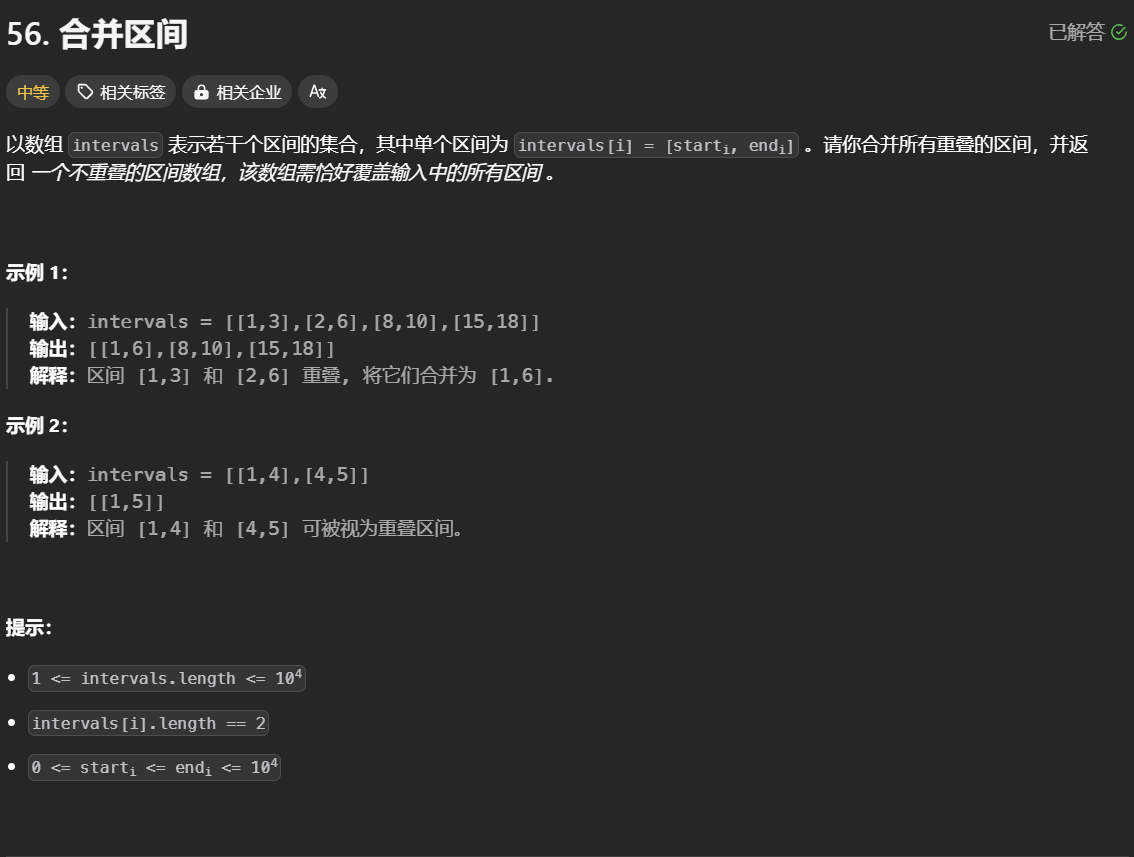
普通做法：可以用一个大数组记录所有区间包含的所有元素，再把这个大数组转化成若干个区间的形式。

进阶做法：先对所有的区间进行排序（按左侧起点大小顺序排序。这里难点在于 Comparator 的语法），而后对于两个区间项前一项的终点>后一项的起点的情况就可以合并。合并结果是 [前一项的起点，Math.max(前一项的终点，后一项的终点)].

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals.length == 0)
            return new int[0][2];

        Arrays.sort(intervals, new Comparator<int[]>() {
            public int compare(int[] interval1, int[] interval2) {
                return interval1[0] - interval2[0];
            }
        });

        List<int[]> result = new ArrayList<int[]>();
        for (int i = 0; i < intervals.length; i++) {
            if (result.size() == 0 || result.get(result.size() - 1)[1] < intervals[i][0]) {
                result.add(new int[] { intervals[i][0], intervals[i][1] });
            } else
                result.get(result.size() - 1)[1] = Math.max(intervals[i][1], result.get(result.size() - 1)[1]);
        }

        return result.toArray(new int[result.size()][]);
    }
}

189. 轮转数组

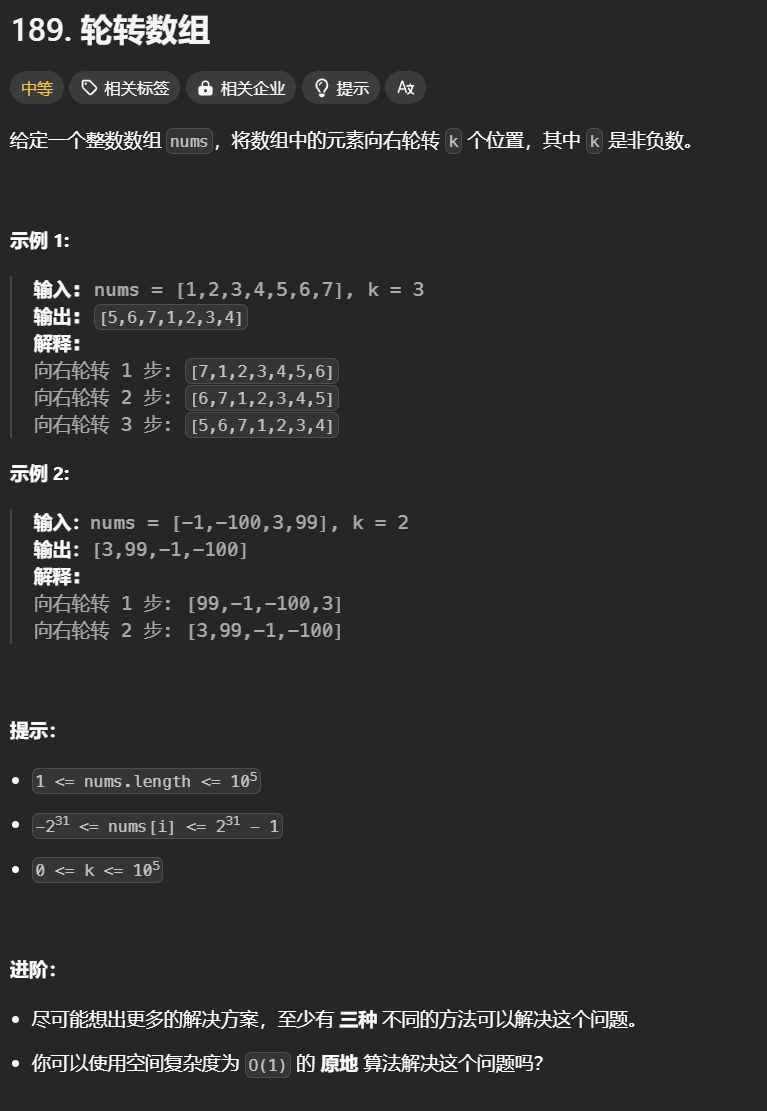
普通做法：开辟一块新的数组区间，把原数组 i 位置元素放到新数组 (i+k)%nums.length 的位置。时间复杂度 O(n) 空间复杂度 O(n).

reverse 做法：数组轮转其实相当于整个数组 reverse 一下，然后 [0, k-1] 区间的子数组 reverse 一下，[k, nums.length-1] 区间的子数组 reverse 一下。这个非常巧妙，最好记住。

class Solution {
    public void rotate(int[] nums, int k) {
        if (nums.length <= 1)
            return;
        k %= (nums.length);
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }

    public void reverse(int[] nums, int L, int R) {
        while (L < R) {
            int temp = nums[L];
            nums[L] = nums[R];
            nums[R] = temp;
            L++;
            R--;
        }
    }
}

还有一种环状替换方法感兴趣的同学可以研究一下。

238. 除自身以外数组的乘积

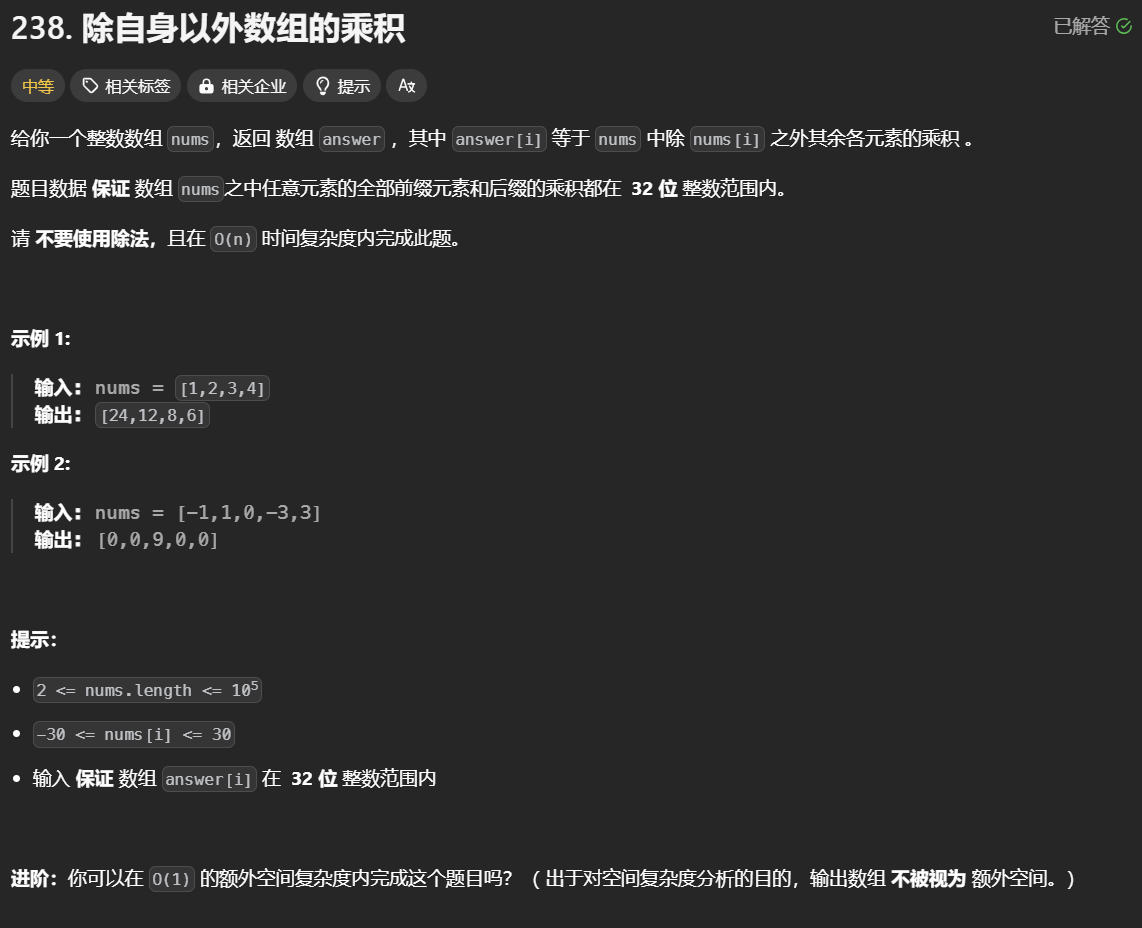
普通做法：O(n^2)，对于新数组每个元素，用原数组所有元素（除对应位置上的元素）遍历相乘获得。或者说是这个元素左侧的所有元素遍历乘积（L[i]）*右侧所有元素遍历乘积（R[i]）。

除法做法（当然题里不让用hh）：先让数组所有元素相乘，然后新数组每个元素=原数组所有元素乘积/原数组该位置上的元素。这里有一种情况需要考虑：原数组中某个元素=0的情况，比如原数组是 [-1,1,0,-3,3]，那么计算新数组 index=2 位置上的元素就不能用原数组所有元素相乘再/0 计算了，乘的时候就要跳过当前位置元素=0的情况。

空间复杂度 O(1) 做法：其实就是再普通做法左右列表乘积的基础上稍做改动。我们可以发现，第i个元素的左侧列表元素乘积=第 i-1 个元素的左侧列表乘积=*第i-1个元素。这样我们就不需要存储每个元素的左侧列表右侧列表了，可以直接用一个 L 变量一个 R 变量迭代获取所有元素的左侧和右侧列表乘积。

思路不难，不过还是要自己能想到才行。

class Solution {
    public int[] productExceptSelf(int[] nums) {
        // left
        int[] ans = new int[nums.length];
        ans[0] = 1;
        for (int i = 1; i < nums.length; i++) {
            ans[i] = ans[i - 1] * nums[i - 1];
        }

        // right
        int R = 1;
        for (int i = nums.length - 2; i >= 0; i--) {
            R *= nums[i + 1];
            ans[i] *= R;
        }

        return ans;
    }
}