理解RLHF与对齐税困境
RLHF的技术脉络与价值对齐挑战
大型语言模型(LLMs)如GPT-4、Claude和Llama等,通过在海量文本数据上的预训练,获得了解决多种任务的能力,包括复杂的推理、常识问答、翻译等。然而,这些预训练模型生成的内容并不总是符合人类的偏好和价值观。为了使LLMs更好地与人类意图保持一致,研究者提出了基于人类反馈的强化学习(Reinforcement Learning from Human Feedback, RLHF)技术,该技术已成为对齐AI系统与人类价值观的主导范式之一。(扩展阅读:大模型偏好对齐强化学习技术:从PPO、GRPO到DPO的演进与创新、ORPO:颠覆传统,偏好对齐的简约革命)
RLHF的典型流程包含三个关键阶段:监督微调(SFT)、奖励模型训练和强化学习微调。在SFT阶段,模型使用人类标注的高质量回答进行有监督学习;随后,训练一个奖励模型来学习对人类偏好进行评分;最后,通过强化学习算法(如PPO)针对奖励模型进行优化,使模型生成更符合人类偏好的输出。(扩展阅读:大模型偏好对齐强化学习技术:从PPO、GRPO到DPO的演进与创新、PPO与GRPO的架构本质:策略优化范式的演进与对比、MTP、MoE还是 GRPO 带来了 DeepSeek 的一夜爆火?)
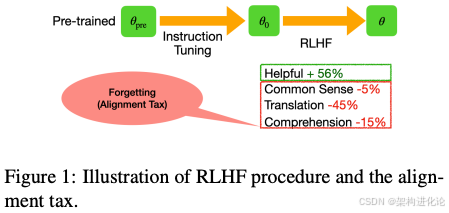
然而,RLHF过程存在一个根本性矛盾——在追求对齐性能的同时,往往会损害模型在预训练阶段获得的基本能力。这一现象被Askell等研究者称为“对齐税”(Alignment Tax)。简单来说,对齐税指的是模型在对齐过程中对预训练知识的遗忘,表现为在多种NLP任务(如常识问答、阅读理解、翻译)上的性能下降。这种遗忘现象在学术文献中也被称为“灾难性遗忘”,即在适应新任务时,模型逐渐失去解决先前任务的能力。
对齐税的问题本质与影响
对齐税的产生根源在于优化目标的冲突。预训练阶段模型通过最大似然估计学习数据的通用分布,而RLHF阶段则通过奖励模型优化策略,使模型偏向特定分布。当这两个目标不一致时,强化学习的优化过程会使模型参数偏离预训练时的最优区域,导致通用能力受损。
从机器学习理论视角看,这可以理解为多目标优化问题:既要最大化对齐奖励,又要最小化对预训练能力的遗忘。但在标准RLHF流程中,只有奖励最大化被明确优化,而能力保留仅通过简单的KL散度惩罚项来约束,这种处理方式显然不足以平衡两个目标。
论文中的实证研究清晰地揭示了对齐税的存在。作者使用OpenLLaMA-3B模型在不同RLHF算法下的实验表明,虽然RLHF提高了模型在人类偏好数据集上的奖励得分,但在多个NLP基准任务(如ARC、Race、PIQA等)上的性能却显著下降。这种权衡关系类似于经济学中的“收益-成本权衡”—要想获得更高的对齐性能,就必须付出更多能力损失的代价。
生活化案例解析:从“全科医生”到“专科医生”
我们可以用一个医疗领域的比喻来理解对齐税:想象一位接受全面培训的全科医生,他具备处理各种疾病的广泛知识。然而,当这位医生专注于成为心脏病专家(相当于RLHF的对齐过程),他可能会逐渐淡忘一些妇产科或皮肤科的专门知识(相当于对齐税)。虽然他成为了更好的心脏病专家,但作为全科医生的综合能力却下降了。
类似的,在商业应用中,一家公司可能希望LLM专门适应其客户服务风格(对齐目标),但同时不希望模型失去处理技术问题、逻辑推理等通用能力(预训练能力)。过高的对齐税会大幅增加企业的模型维护成本,因为他们需要为保留通用能力而额外准备多个专用模型。
模型平均化的创新方法
简单却有效的基础方案:模型平均化
面对对齐税的挑战,论文《Mitigating the Alignment Tax of RLHF》提出了一个看似简单却极为有效的解决方案——模型平均化(Model Averaging)。该方法的核心思想是:将预训练模型权重与对齐后模型权重进行线性插值,从而在参数空间中找到一个平衡点,同时保留对齐性能和预训练能力。
具体而言,给定预训练模型参数θ_pre和RLHF微调后的参数θ_rlhf,模型平均化通过以下公式计算新参数:
θ_avg = α · θ_rlhf + (1 - α) · θ_pre
其中α是插值系数,控制着对齐程度与能力保留的平衡。当α=1时,模型完全使用对齐后的参数;当α=0时,则回退到原始预训练模型。通过调整α值,我们可以在对齐税和对齐奖励之间找到不同的权衡点。
值得注意的是,这种方法不需要重新训练模型,只需对模型权重进行简单的算术组合,计算成本极低。实验结果显示,这种简单的平均化策略出人意料地构建了最优的奖励-税收帕累托前沿(Pareto front),即在相同对齐税水平下获得更高的奖励,或在相同奖励水平下产生更少的遗忘。
理论洞察:特征多样性的增强
为什么简单的模型平均化能如此有效?论文提供了深度的理论分析:平均化通过增强特征多样性来改善模型的多任务性能。在神经网络中,不同任务依赖于相关的特征表示,当模型针对新任务(对齐)进行优化时,可能会扭曲那些被原有任务(预训练能力)所依赖的特征。
模型平均化实际上在参数空间中创建了一个“中间模型”,该模型保留了两种任务所需的特征表示。从数学角度看,平均化操作相当于在特征空间中增加了基模型的特征方向,从而扩大了模型能够有效覆盖的特征范围。当不同任务(对齐和预训练任务)共享部分特征空间时,这种特征多样性尤其有益。
论文进一步指出,Transformer架构的不同层对平均化的响应各不相同。较低层次的嵌入层和注意力机制更倾向于捕捉通用语言特征,而较高层次的网络则更专注于特定任务特征。因此,对不同网络层使用不同的平均化系数可能会带来更好的效果。
异构模型平均化(HMA)算法
基于上述观察,论文提出了异构模型平均化(Heterogeneous Model Averaging,HMA)算法。与简单的全局平均化不同,HMA为Transformer架构的不同层分配不同的平均化系数,从而实现更精细的权衡控制。
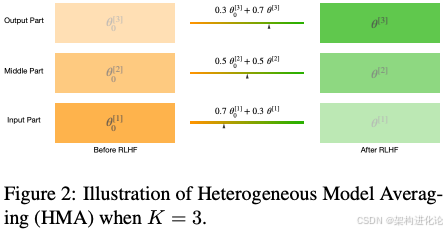
HMA算法的核心公式如下:
θ_hma = {α_i · θ_rlhf_i + (1 - α_i) · θ_pre_i | i ∈ [1, L]}
其中L是Transformer的总层数,α_i是第i层的插值系数。通过为不同层分配不同的α_i值,我们可以精确控制每层保留预训练特征的程度。
下图展示了HMA算法的整体架构设计:
HMA的实现需要解决一个关键问题:如何确定各层的最佳插值系数。论文提出了两种方法:(1)基于梯度的优化方法,将分层系数作为可学习参数,通过梯度下降优化奖励-税收权衡;(2)进化策略方法,通过多目标进化算法直接搜索帕累托前沿上的最优系数组合。
代码实现详解
以下代码示例展示了HMA算法的核心实现,包含了分层平均化和系数优化过程:
import torch
import torch.nn as nn
from transformers import AutoModelForCausalLM
from typing import Dict, List, Tuple
import numpy as np
class HeterogeneousModelAveraging:
"""
异构模型平均化 (HMA) 实现
该方法通过分层权重插值,在RLHF对齐模型中保留预训练能力,
实现对对齐税的有效控制
"""
def __init__(self,
pretrained_model: nn.Module,
rlhf_model: nn.Module,
layer_names: List[str]):
"""
初始化HMA
Args:
pretrained_model: 预训练模型实例
rlhf_model: RLHF微调后的模型实例
layer_names: 需要平均化的层名称列表
"""
self.pretrained_model = pretrained_model
self.rlhf_model = rlhf_model
self.layer_names = layer_names
# 初始化分层插值系数(全设为0.5)
self.alpha_dict = {name: 0.5 for name in layer_names}
def compute_heterogeneous_average(self) -> nn.Module:
"""
计算分层权重平均值
Returns:
averaged_model: 平均化后的模型实例
"""
# 创建模型副本作为基础
averaged_model = type(self.pretrained_model)()
averaged_model.load_state_dict(self.pretrained_model.state_dict())
averaged_state_dict = averaged_model.state_dict()
pretrained_state_dict = self.pretrained_model.state_dict()
rlhf_state_dict = self.rlhf_model.state_dict()
# 对每一层进行异构平均化
for layer_name in self.layer_names:
if layer_name in pretrained_state_dict:
alpha = self.alpha_dict[layer_name]
# 核心平均化公式:θ_avg = α * θ_rlhf + (1-α) * θ_pre
averaged_weight = (alpha * rlhf_state_dict[layer_name] +
(1 - alpha) * pretrained_state_dict[layer_name])
averaged_state_dict[layer_name] = averaged_weight
averaged_model.load_state_dict(averaged_state_dict)
return averaged_model
def evaluate_alignment_tax(self,
model: nn.Module,
evaluation_tasks: Dict) -> Dict[str, float]:
"""
评估模型在对齐税方面的表现
Args:
model: 待评估的模型
evaluation_tasks: 评估任务字典
Returns:
metrics: 各任务评估指标
"""
metrics = {}
# 在多个基准任务上评估模型性能
for task_name, task_data in evaluation_tasks.items():
# 任务评估逻辑(具体实现取决于任务类型)
task_score = self._evaluate_on_task(model, task_data)
metrics[task_name] = task_score
return metrics
def optimize_coefficients(self,
reward_eval_func,
tax_eval_func,
target_reward: float = None,
max_iterations: int = 100) -> Dict[str, float]:
"""
优化分层系数以找到最优的奖励-税收权衡
Args:
reward_eval_func: 对齐奖励评估函数
tax_eval_func: 对齐税评估函数
target_reward: 目标奖励值(可选)
max_iterations: 最大优化迭代次数
Returns:
optimized_alphas: 优化后的分层系数
"""
best_alphas = self.alpha_dict.copy()
best_tax = float('inf')
for iteration in range(max_iterations):
# 生成新的系数候选集
candidate_alphas = self._generate_candidate_alphas()
for alpha_candidate in candidate_alphas:
self.alpha_dict = alpha_candidate
current_model = self.compute_heterogeneous_average()
# 评估对齐奖励和对齐税
reward = reward_eval_func(current_model)
tax = tax_eval_func(current_model)
# 多目标优化:在满足奖励约束下最小化对齐税
if target_reward is None:
# 没有目标奖励时,优化综合得分
score = reward - tax
if score > best_tax:
best_tax = score
best_alphas = alpha_candidate.copy()
else:
# 有目标奖励时,在满足奖励条件下最小化税
if reward >= target_reward and tax < best_tax:
best_tax = tax
best_alphas = alpha_candidate.copy()
# 早期停止条件检查
if self._check_convergence():
break
self.alpha_dict = best_alphas
return best_alphas
def _generate_candidate_alphas(self) -> List[Dict[str, float]]:
"""
生成分层系数候选集
使用进化策略生成围绕当前最佳系数的变异候选
"""
candidates = []
for _ in range(10): # 生成10个候选
candidate = {}
for layer, alpha in self.alpha_dict.items():
# 添加高斯噪声探索新系数
new_alpha = alpha + np.random.normal(0, 0.1)
# 将系数裁剪到[0,1]范围内
new_alpha = np.clip(new_alpha, 0.0, 1.0)
candidate[layer] = new_alpha
candidates.append(candidate)
return candidates
# 使用示例
def demonstrate_hma_usage():
"""
展示HMA使用方法
"""
# 加载预训练模型和RLHF模型
pretrained_model = AutoModelForCausalLM.from_pretrained("openlm-research/open_llama_3b")
rlhf_model = AutoModelForCausalLM.from_pretrained("path/to/rlhf/model")
# 定义需要平均化的Transformer层
layer_names = [
'model.embed_tokens.weight', # 嵌入层
'model.layers.0.input_layernorm.weight', # 底层编码器
'model.layers.5.input_layernorm.weight', # 中层编码器
'model.layers.11.input_layernorm.weight', # 高层编码器
'lm_head.weight' # 输出层
]
# 初始化HMA
hma = HeterogeneousModelAveraging(pretrained_model, rlhf_model, layer_names)
# 优化分层系数
def reward_eval_func(model):
# 简化的奖励评估,实际应使用偏好模型
return np.random.random() # placeholder
def tax_eval_func(model):
# 简化的对齐税评估,实际应在多个基准任务上测试
return np.random.random() # placeholder
optimized_alphas = hma.optimize_coefficients(reward_eval_func, tax_eval_func)
# 使用优化后的系数创建最终模型
final_model = hma.compute_heterogeneous_average()
return final_model上述代码展示了HMA算法的核心实现,重点在于分层权重插值和系数优化两个关键过程。在实际应用中,评估函数需要根据具体任务实现,通常包括在多个基准数据集上的测试和使用奖励模型进行偏好评分。
实验评估与效果验证
实验设置与基准测试
为了全面评估HMA方法的有效性,论文设计了严格的实验方案。实验使用OpenLLaMA-3B和Mistral-7B作为基础模型,涵盖了多种RLHF算法(包括PPO、DPO等),并在14个不同的基准测试上验证方法性能。
评估体系分为两个主要维度:
-
对齐奖励:使用训练好的奖励模型评估模型输出符合人类偏好的程度
-
对齐税:通过在一系列NLP任务(如ARC、Race、PIQA、SQuAD等)上的性能变化来衡量预训练能力的保留程度
实验对比了多种方法,包括:原始RLHF、L2正则化、EWC(Elastic Weight Consolidation)、 replay缓冲方法和简单的模型平均化等,确保比较的全面性。
性能结果与分析
实验结果显示,HMA方法在奖励-税收帕累托前沿上达到了最佳平衡。具体来说,在相同对齐税水平下,HMA能够获得更高的对齐奖励;反之,在相同奖励水平下,HMA引发更少的预训练能力遗忘。
以下表格展示了在OpenLLaMA-3B模型上的部分实验结果:
| 方法 | 对齐奖励 | 常识QA准确率 | 阅读理解F1 | 翻译BLEU |
|---|---|---|---|---|
| 预训练基础模型 | 0.0 | 45.2 | 78.5 | 32.1 |
| 标准RLHF | 0.75 | 38.6 | 70.3 | 26.8 |
| 简单模型平均化 | 0.68 | 42.7 | 75.2 | 30.5 |
| HMA | 0.72 | 43.5 | 76.1 | 31.2 |
从表中可以看出,与标准RLHF相比,HMA方法在仅牺牲少量对齐奖励(0.75 vs 0.72)的情况下,显著减少了对齐税,在常识QA、阅读理解和翻译等任务上性能明显优于标准RLHF。
分层系数的关键发现
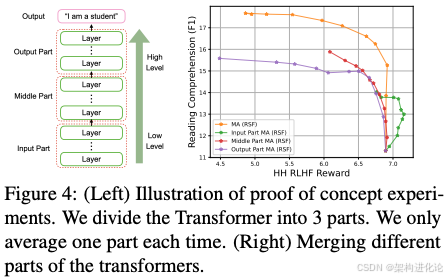
论文中一个重要的发现是:不同层的最佳插值系数存在显著差异。具体而言:
-
底层Transformer层(接近嵌入层)更适合使用较低的α值(约0.3-0.5),即更多保留预训练参数
-
中层Transformer层通常使用中等α值(约0.5-0.7)
-
高层Transformer层和输出层可以使用较高的α值(约0.7-0.9),即更多采用RLHF参数
这一发现与神经网络的可解释性研究一致:底层通常学习通用语言特征,而高层更专注于任务特定特征。因此,在平均化过程中保留底层预训练参数对维持模型通用能力更为重要。
消融实验与扩展性验证
为了验证HMA各个组件的重要性,论文进行了系统的消融实验:
-
均匀平均化vs异构平均化:实验表明,为不同层分配不同系数的异构平均化明显优于统一系数的方法,在奖励-税收权衡上前者帕累托前沿完全占优后者。
-
系数优化必要性:与随机选择的系数相比,通过优化得到的系数能带来显著性能提升,说明系数选择不是微不足道的。
-
跨模型扩展性:HMA方法在从OpenLLaMA-3B到Mistral-7B的不同规模模型上都表现一致优秀,表明该方法不依赖于特定模型架构。
-
算法兼容性:HMA与多种RLHF算法(PPO、DPO、KTO等)兼容,在不同算法基础上都能带来一致的改进。
这些实验充分证明了HMA方法的有效性、通用性和必要性。
技术影响与未来展望
对RLHF研究与实践的影响
HMA方法对RLHF研究和实践带来了重要影响。首先,它揭示了参数空间平均化这一简单技术在对齐税问题上的惊人潜力,为后续研究提供了新方向。传统方法多基于约束优化或正则化,而HMA展示了对参数空间的直接干预可以更有效地控制模型行为。
其次,HMA的分层异质性设计深化了我们对Transformer架构工作机制的理解。通过区别对待不同层,我们能够更精细地控制模型行为,这为未来的模型优化技术提供了重要借鉴。
在实际应用方面,HMA提供了一种计算高效的解决方案。与复杂的正则化方法或需要保留数据的replay方法相比,HMA只需简单的参数操作,计算成本几乎可以忽略不计,这对工业界部署大型模型尤其具有吸引力。
局限性与发展方向
尽管HMA表现优秀,但仍存在一些局限性。首先,系数优化过程仍然计算成本较高,需要多次评估模型性能。未来研究可以探索更高效的系数预测方法,例如通过元学习或理论分析直接给出接近最优的系数。
其次,当前HMA主要处理单一预训练模型和单一RLHF模型的插值,但实际应用中可能存在多个专业模型。扩展HMA到多模型融合场景,实现“模型集合”的能力,将是有价值的研究方向。
另外,HMA的理论基础仍有待加强。虽然论文提供了一些理论分析,但对平均化为什么有效的深入理解还需要进一步的工作,这有助于改进方法并预测其行为。
产业应用前景
HMA技术在AI产业中具有广阔的应用前景:
-
定制化AI助手:企业可以在保持模型通用能力的同时,定制符合自己需求和风格的AI助手,无需担心专业化导致的性能下降。
-
安全对齐:在实施安全对齐时,可以使用HMA平衡安全性和模型能力,避免过度对齐导致的模型“弱化”。
-
持续学习:HMA为LLMs的持续学习提供了新思路,通过平均化不同阶段的模型,可以累积知识同时减少遗忘。
-
模型部署:云服务提供商可以使用HMA快速生成满足不同客户需求的模型变体,而无需为每个客户重新训练模型。
伦理与社会考量
如同任何技术进展,HMA也带来了一些伦理和社会考量。一方面,它使AI系统更容易根据人类价值观进行对齐,这是积极的;另一方面,它也可能被用于创建更符合特定群体价值观但可能对社会整体不利的模型。
此外,减少对齐税意味着专业化的模型仍保持广泛的能力,这可能增加模型误用的风险。因此,在发展这些技术的同时,需要建立相应的治理框架和使用规范,确保技术向善发展。
结论
论文《Mitigating the Alignment Tax of RLHF》通过对齐税问题的系统分析,提出了简单却有效的异构模型平均化方法(HMA),在RLHF研究中迈出了重要一步。本文详细解读了HMA的创新设计、理论依据、实现方法和实验效果。
HMA的核心洞见在于:通过分层权重插值,在参数空间中找到预训练能力和对齐性能的最佳平衡点。这一方法不仅有效解决了对齐税问题,而且计算高效、易于实现,为工业界提供了实用的解决方案。
从更广的视角看,HMA代表了AI对齐研究的一个新方向——通过模型参数操作而非仅通过优化过程来控制模型行为。这一思路可能会启发更多创新方法,推动AI对齐领域的发展。
随着大型语言模型在社会中的应用日益广泛,如何平衡专业化与通用性、对齐与能力将成为关键问题。HMA为我们提供了解决这一挑战的有力工具,助力构建既符合人类价值观又保持广泛能力的AI系统。























 469
469

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










