ATTENTION, LEARN TO SOLVE ROUTING PROBLEMS! 使用强化学习解决tsp问题（一）Seq2Seq的前生今世

实习的时候，接触到了使用强化学习去解决tsp的问题，开始先读了ATTENTION, LEARN TO SOLVE ROUTING PROBLEMS! 这篇文章，文章里更改了Transformer Architecture，并搭载了强化学习中的greedy rollout baseline去解决tsp的问题。无奈背景知识太少，也没有接触过强化学习相关的知识，读起来很费劲。经过请教公司的前辈，制定了下面的学习策略。

• 前期准备工作

• Dzmitry Bahdanau的NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE

• 这一篇文献介绍了传统的seq2seq的问题无法解决长语句输入的问题，作者提出了一个叫“align and translate jointly”的解决方案，其实就是一个注意力机制，简单来说就是在预测一个目标词汇的时候，可以查到源语言序列中的哪一部分与它相对应，在后续查找生词中可以直接复制相对应的源语言。
• 这篇csdn博文把注意力机制的作用解释的很清楚https://blog.youkuaiyun.com/weixin_40240670/article/details/86483896。借用文章中的原句解释，“Attention Mechanism的作用就是将encoder的隐状态按照一定权重加和之后拼接（或者直接加和）到decoder的隐状态上，以此作为额外信息，起到所谓“软对齐”的作用，并且提高了整个模型的预测准确度。简单举个例子，在机器翻译中一直存在对齐的问题，也就是说源语言的某个单词应该和目标语言的哪个单词对应，如“Who are you”对应“你是谁”，如果我们简单地按照顺序进行匹配的话会发现单词的语义并不对应，显然“who”不能被翻译为“你”。而Attention Mechanism非常好地解决了这个问题。如前所述，Attention Mechanism会给输入序列的每一个元素分配一个权重，如在预测“你”这个字的时候输入序列中的“you”这个词的权重最大，这样模型就知道“你”是和“you”对应的，从而实现了软对齐”。
• 文中的encoder和decoder结构和seq2seq类似，不同的是encoder里的RNN是双向的，有一个前向的RNN和一个后向的RNN。前向RNN通过正向读取输入序列来计算前向隐藏层状态h->；后向RNN通过反向读取输入序列来计算反向隐藏层状态h<-。然后在j时刻的输入xj的前向隐藏层状态hj->和反向隐藏层状态hj<-组成了xj的注解（annotation）。  
• Decode里有一个上下文向量Ci，上下文向量的计算由一系列注解（h1,...hT）加权求和计算出来。如下图，最后计算出得分函数eij以及注意力向量a。

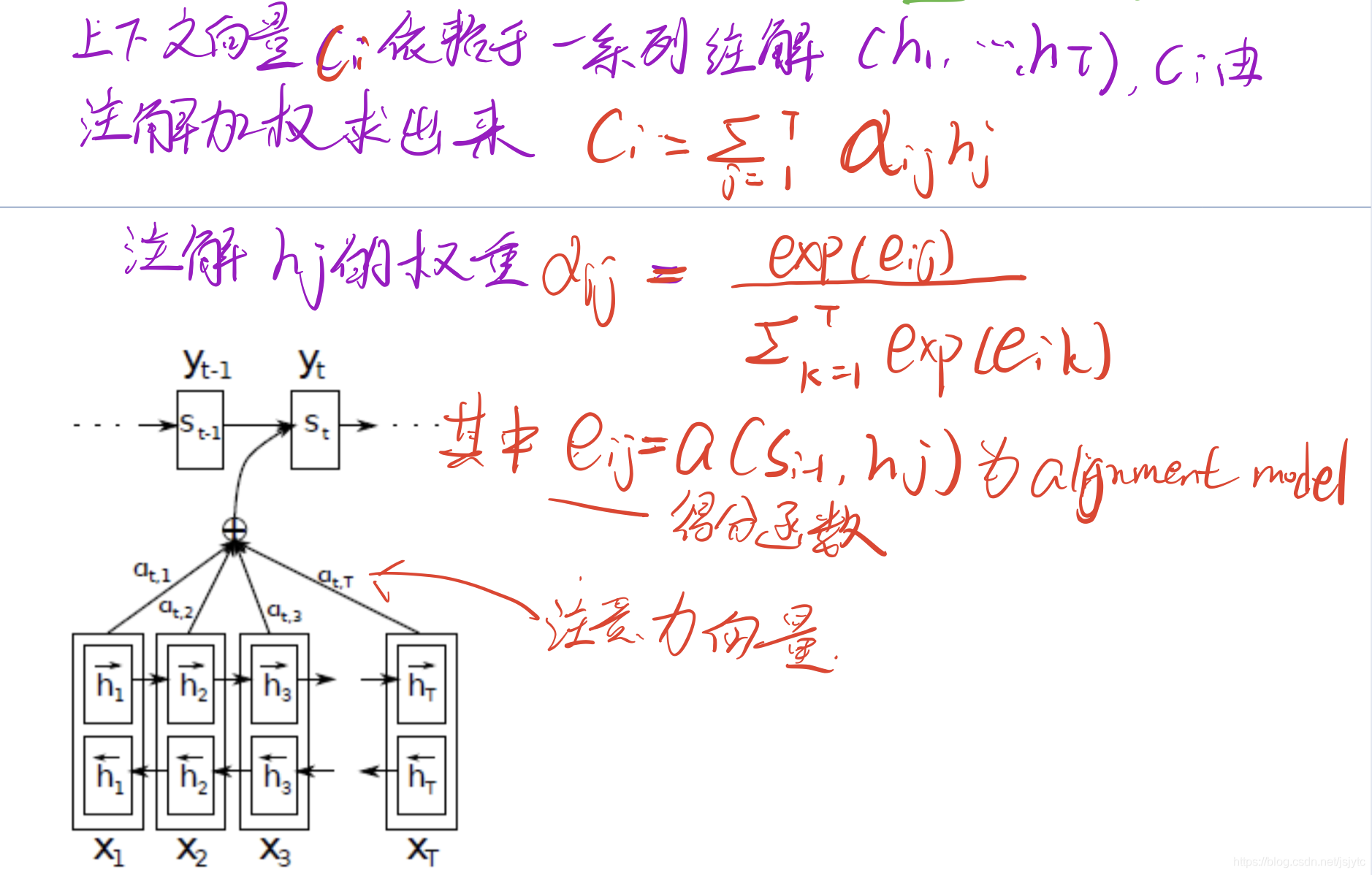
• Oriol Vinyals∗​​​​​​的Pointer Networks

• 这一篇文献首先提出了Bahdanau的缺陷，缺陷就是“still require the size of the output dictionary to be fixed a priori”，我理解的就是需要预先定义知道输出字典的长度，即输出序列的长度无法自适应输入序列的长度。Vinyals提出了一个架构叫pointer networks解决了这一问题，原理就是在每次预测一个元素的时候找到输入序列中权重最大的那个元素，然后把权重最大的元素输出，这样就可以解决输出序列长度必须固定的问题了。

下一篇还是前期准备工作，会介绍一些强化学习的背景知识。