基础矩阵

一、基础矩阵原理介绍
基本矩阵体现了两视图几何（对极几何，epipolar geometry）的内在射影几何（projective geometry）关系，基本矩阵只依赖于摄像机的内参KK和外参R,tR,t。

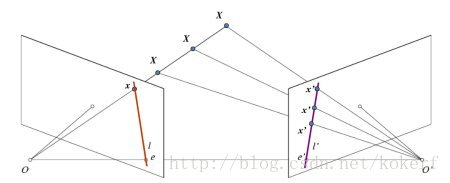
上图是一个两视图的几何描述，其中OO、O′O′是两个相机的光心，两点连线OO′OO′称为基线，基线与图像平面的交点ee、e′e′称为对极点，其中ll、l′l′分别是图像点x′x′、xx对应的对极线。

上图的左侧相机的图像平面上的一个点xx，反向投影得到射线OXOX。由于点的深度未知，图像平面上的点xx可能是射线上某一深度的3D点XX。而射线OXOX在第二个相机的图像平面上的投影为l′l′。也就是说，给定一对图像，第一幅图像上的每个点xx，在另外一幅图像上存在一条直线l′l′与之对应。换言之，第二幅图像上与点xx对应的点x′x′必定在线l′l′上。

我们可以看到这里存在一个从一副图像上的点到另外一幅图像与之对应的对极线的映射x→l′x→l′。而基本矩阵就表示了这种从点到直线的射影映射关系。

几何推导
　　 首先在几何层面对上述一个图像上的点到另外一个图像上的对极线的映射关系进行分析。可以把这个映射分成两个步骤：
点到平面的转移
　　 存在一个不经过两个相机光心的的平面ππ，光心OO与xx的射线与平面ππ相交与一点XX。该点XX又投影到第二幅图像平面上的点x′x′。这个称为点xx通过平面ππ的转移。点xx，x′x′是平面ππ上的3D点XX在两个相机平面上的像。对应每一个3D点XX都存在一个2D的单应HπHπ把每一个xx映射到x′x′。
对极线的构造
　　已知第二幅图像上的对应点x′x′，再加上对极点e′e′我们可以构造对极线l′=e′×x′=[e′]×x′l′=e′×x′=[e′]×x′（这里的[e′]×[e′]×是叉乘矩阵）。由于x′x′可以表示为x′=Hπxx′=Hπx，则有：
l′=[e′]×Hπx=Fx