标定相机参数-张正友方法

一、实验原理
1.计算外参
设三维世界坐标的点为M=[X,Y,Z,1]T，二维相机平面像素坐标为m=[u,v,1]T，所以标定用的棋盘格平面到图像平面的单应性关系为： sm=A[R,t]M
其中

不妨设棋盘格位于Z = 0，定义旋转矩阵R的第i列为 ri, 则有：

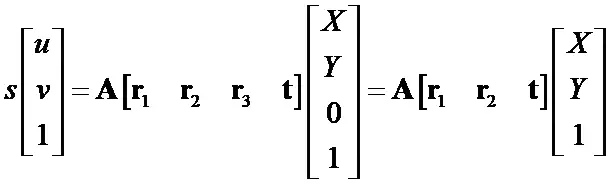
令H=[h1 h2 h3]=λA[r1 r2 t]
于是空间到图像的映射可改为： sm=HM，
其中H是描述Homographic矩阵，H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H

外参具体计算公式。注意：R3是 t
一般而言，求解出的R = [r1 r2 t] 不会满足正交与归一的标准
在实际操作中，R 可以通过SVD分解实现规范化(详见原文)

2.计算内参
由r1和r2正交，且r1和r2的模相等，可以得到如下约束：

正交
模相等
可以推到出