本文介绍了相机标定中内参的获取方法，包括理论和实践两部分。通过使用棋盘图，利用最少3幅图像和4个特征点求解单应矩阵，进而计算相机的内部参数和畸变参数。文章详细阐述了内参标定的步骤，涉及单应矩阵的构建、最小二乘法求解以及如何从B矩阵求得内参矩阵A。
相机标定，获取内参
至少3幅影响（求B，6参数，每幅影像对应求2个），每幅影像至少4个特征点（求H，8参数，每个特征点对应求2个）
参考资料：https://blog.youkuaiyun.com/zkl99999/article/details/48372203?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
https://blog.youkuaiyun.com/a6333230/article/details/83478064
理论1
相机标定分：内参标定、外参标定、c矩阵
内参标定：采用棋盘图或者点阵图，将相机固定（焦距、光圈等内部元素）。用相机拍摄多组不同角度的棋盘图，这点和普通的matlab的棋盘图标定类似。matlab利用棋盘图标定，它也给出了标定的外参，但是给定的并非我们所求，而是将世界坐标系定在了棋盘图上，我们需要的世界坐标系是固定不变的或者至少是与相机的相对位置不会发生改变。
内参标定输入为：像素坐标u、v和世界坐标x、y、z，该z没有定义具体的数值，因为在此处的求解不会应用到，并且我们此步也无法求得。那么这些参数怎么来的呢？u、v为图像中棋盘格的角点坐标，与其对应的x、y表示该角点在整个棋盘图下的坐标，该坐标系定在棋盘图上，因此我们拍摄5次图像，这些图像相应的坐标应该相同。为了计算时数据的变换较为方便，这里z也给出，值给0或1都行，不影响计算。
内参标定输出为：内部参数+相机畸变参数。内部参数：fu、fv、u、v；相机畸变参数：k1，k2
内参求解步骤：
1.求单应矩阵
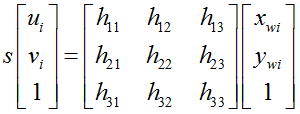
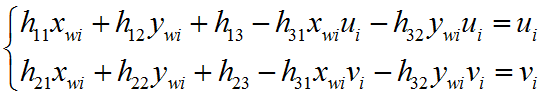
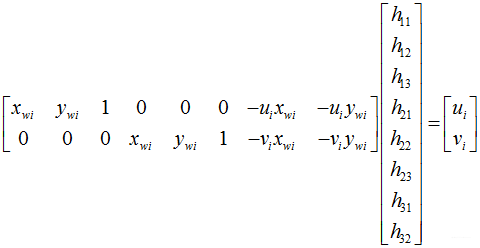
这里的h33设置为1……课本中给出的理由是它可以设置为任意数，二郎也和同事讨论过，没有定论，有一种理解有道理：计算中h33能都提到右边，那么在根据公式进行求解时，它变成几，都是对所有公式进行操作的，因此公式之间的关系不会发生改变，所求出来代表关系的h参数也不会受到影响，只是按h33进行了缩放。
比如：两边先同时除以h33（由于没有找到这里的h33=1的解释，因此二郎做了这种假设）
每个特征点，可以求得两个方程。这里有8个未知数，因此可以用4个特征点完成求解。
这里用到了棋盘格，在一张棋盘格图中，我们得到了很多（u，v）与（x，y）的对应，因此可以解出我们的单应矩阵。
这里每个棋盘格图对应了一个单应矩阵，这些单应矩阵主要的不同在于（R，t），每个棋盘图都有自己的世界坐标系，原点在棋盘图的一个角点上，这个matlab内部程序已经指定，一般情况下为左上角。此处单应矩阵的求解用到的最小二乘法。下面的推导和求解，均是建立在单应矩阵已知的情况下进行的。
实践1
1.拍摄标定板照片
function CreatePlate()
J = (checkerboard(300,3,4)>0.5); %生成黑白棋盘图像
figure, imshow(J) %显示黑白棋盘图像
imwrite(J,'plate.jpg'); %保存黑白棋盘图像
end
然后手机拍照存储作为相机拍摄的标定板照片
设照片名称为“MyPlate1.jpg”
2.标定板角点检测
harris算法
function Myharris()
X = imread('MyPlate1.jpg'); % 读取图像
% figure,imshow(X); %在窗口1中打开原始图像
Info = imfinfo('MyPlate1.jpg'); %获取图像相关信息
if (Info.BitDepth > 8)
f = rgb2gray(X); %若图像的位深大于8，则用rgb2gray将彩色图像转换为灰度图像
end
%计算图像亮度f(x,y)在点(x,y)处的梯度-----------------------------------------------
ori_im = double(f) / 255; %unit8转化为64位双精度double64，取值在0~1
fx = [-2 -1 0 1 2]; % x方向梯度算子(用于Harris角点提取算法)
fy = [-2; -1; 0; 1; 2]; % y方向梯度算子(用于Harris角点提取算法)
gx = filter2(fx, ori_im); % x方向滤波
gy = filter2(fy, ori_im); % y方向滤波
%构造自相关矩阵---------------------------------------------------------------
gx2 = gx .^ 2;
gy2 = gy .^ 2;
gxy = gx .* gy;
% clear gx;
% clear gy;
h= fspecial('gaussian', [7 7], 0.6); % 产生5*5的高斯窗函数，sigma取值在0.3~0.9，此处取0.6
gx2 = filter2(h,gx2);
gy2 = filter2(h,gy2);
gxy = filter2(h,gxy);
%提取特征点---------------------------------------------------------------
[height,width]=size(ori_im); %读取图像的高和宽
result = zeros(height, width); % 纪录角点位置，角点处值为1
I = zeros(height, width);
Imax = 0; % 图像中最大的R值
k = 0.2; %k为常系数，经验取值范围为0.04~0.06
for i = 1 : height
for j = 1 : width
M = [gx2(i, j) gxy(i, j); gxy(i, j) gy2(i, j)]; % auto correlation matrix
I(i,j) = det(M) - k * (trace(M)) ^ 2; % 计算R
if I(i,j) > Imax
Imax = I(i, j);
end;
end;
end;
T = 0.06 * Imax;%固定阈值，当R(i, j) > T时，则被判定为候选角点
%在计算完各点的值后，进行局部非极大值抑制-------------------------------------
cnt = 0;
for i = 2 : height-1
for j = 2 : width-1
% 进行非极大抑制，窗口大小3*3
if (I(i, j) > T && I(i, j) > I(i-1, j-1) && I(i, j) > I(i-1, j) && I(i, j) > I(i-1, j+1) && I(i, j) > I(i, j-1) && ...
I(i, j) > I(i, j+1) && I(i, j) > I(i+1, j-1) && I(i, j) > I(i+1, j) && I(i, j) > I(i+1, j+1))
result(i, j) = 1;
cnt = cnt+1;
end;
end;
end;
[posc, posr] = find(result == 1);%返回矩阵result元素等于1处的横纵坐标，就是图像中的角点
disp(cnt); %输出角点个数
figure,imshow(X); %在窗口2中打开提取特征点的图像
hold on; %保留当前窗口的图像，再画另一幅图，使叠加显示
plot(posr, posc, 'ro'); %将图像中找到的角点用品红色的星号标出
uv=[posc, posr] ;
disp(uv);
end
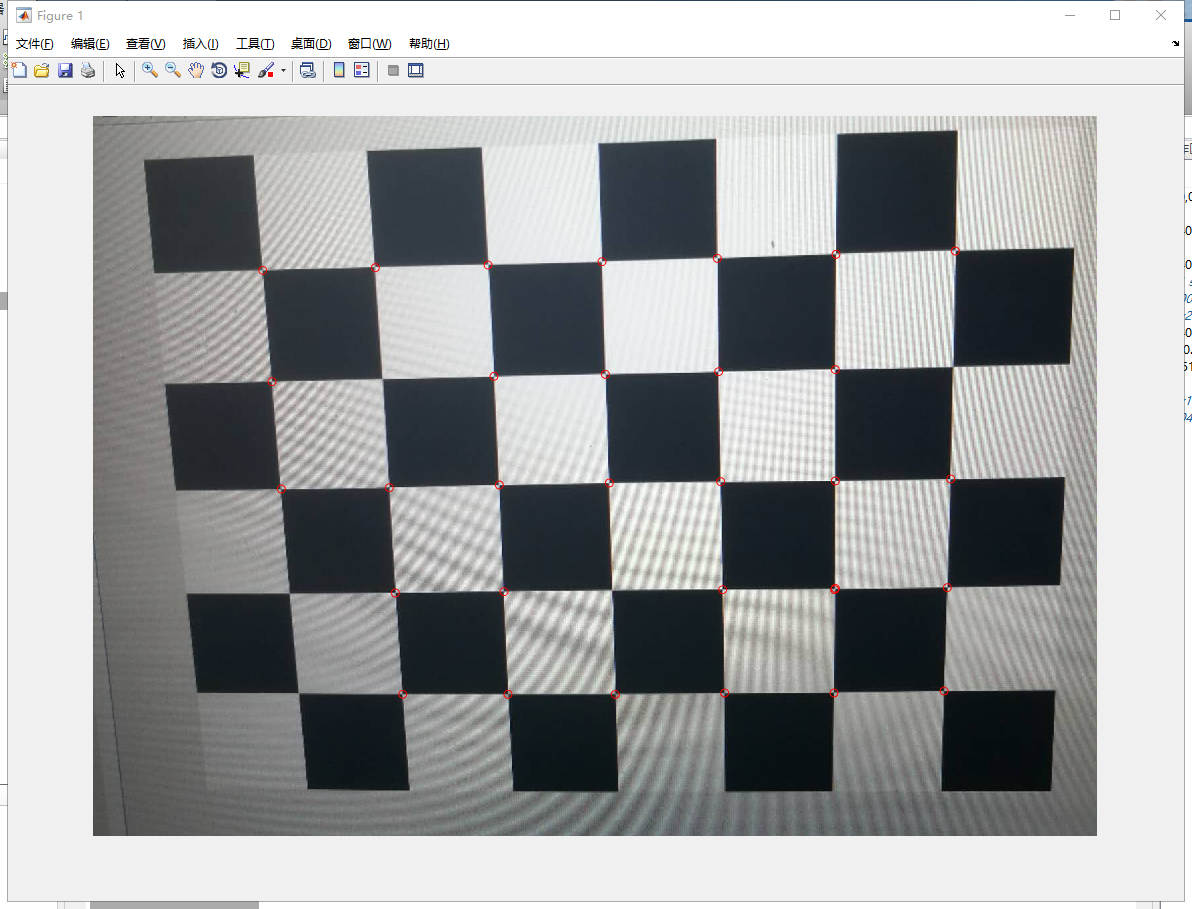
并存储了检测到的角点坐标
uv=[232 255
399 269
560 283
228 424
558 445
716 454
868 465
224 593
391 602
554 610
714 617
868 623
219 764
388 769
551 775
868 784
214 937
384 939
549 942
711 945
866 948
208 1115
381 1114
548 1114
710 1114
866 1112
203 1294
545 1287
708 1282
863 1277];
xy=[-30 20
-30 10
-30 0
-20 20
-20 0
-20 -10
-20 -20
-10 20
-10 10
-10 0
-10 -10
-10 -20
0 20
0 10
0 0
0 -20
10 20
10 10
10 0
10 -10
10 -20
20 20
20 10
20 0
20 -10
20 -20
30 20
30 0
30 -10
30 -20];
超定方程最小二乘解法：
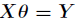
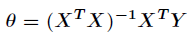
function H=MyFunSolveHomography(uv,xy)
[count,~]=size(uv);
matrix_uv=zeros(count*2,1);
matrix_fxy=zeros(count*2,1);
u=0;
v=0;
x=0;
y=0;
for i=1:count
u=uv(i,1);
v=uv(i,2);
x=xy(i,1);
y=xy(i,2);
matrix_uv(i*2-1,1)=u;
matrix_uv(i*2,1)=v;
matrix_fxy(i*2-1,1:8)=[x,y,1,0,0,0,-u*x,-u*y];
matrix_fxy(i*2,1:8)=[0,0,0,x,y,1,-v*x,-v*y];
end
result=inv(matrix_fxy'*matrix_fxy)*matrix_fxy'*matrix_uv;
H=[result(1,1) result(2,1) result(3,1)
result(4,1) result(5,1) result(6,1)
result(7,1) result(8,1) 1];
end
H=[ -0.6017 -17.1080 552.9464
16.2357 -1.7699 774.8146
-0.0006 -0.0016 1.0000]
理论2
2.单应矩阵构造v，进行B的求解
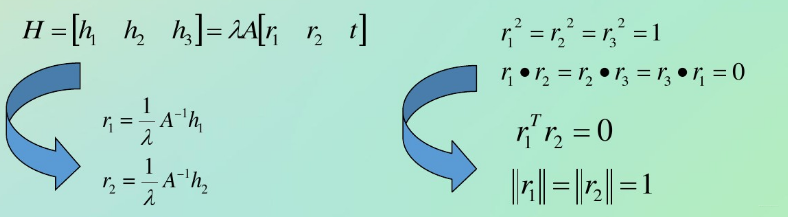这里有人会不理解，r1=和r2=是怎么来的？其实自己可以推导一下，把A设成[3X3]的矩阵，乘进去，应该能够看到，组成了[Ar1 Ar2 Ar3]，它们互相还是独立的。至于为什么A到A逆，这个是最基本的转换，左右同时左乘A逆，看一下，是不是变过来了。
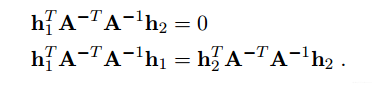
这里的A矩阵为内参矩阵，上面两个式子其实不难证明，
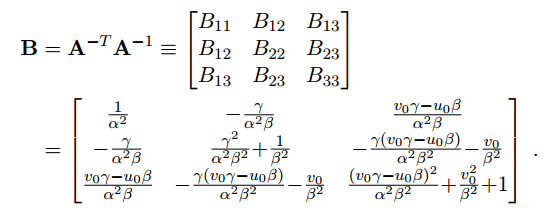
由于B为对称矩阵，因此B中元素可以写为
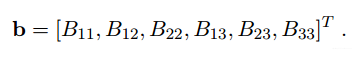
大家可以从上面看到B是由A矩阵组成的，那们A的组合满足的关系，B也满足
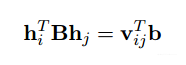
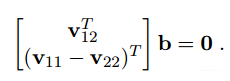
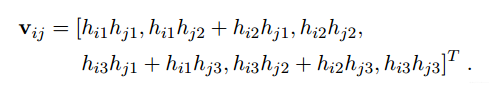
V的由来……大部分文献都没有提到，其实比较简单，直接计算hBh，计算完构造vb，b已经在前面定义。
后面的vb等于0的两项也来自前面约束条件
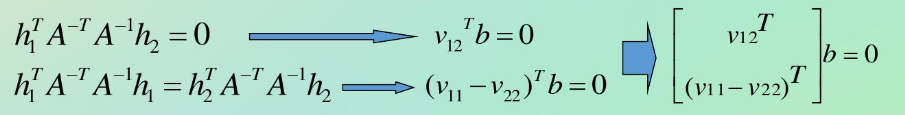
用奇异值分解最小奇异值对应的特征向量便可以表示为b
[u s v]=svd(V); %用正交分解解出b
b=v(:,6);
注意：
这个方程组的本质和前面那两个用h和A组成的约束条件方程组是一样的。在此重复一遍解释：如果我们想完全解出这五个未知量，则需要3个单应性矩阵。3个单应性矩阵在2个约束下可以产生6个方程。这样可以解出全部的五个内参了。大家想一下，我们怎样才能获得三个不同的单应性矩阵呢？答案就是，用三幅标定物平面的照片。我们可以通过改变摄像机与标定板间的相对位置来获得三张不同的照片。（当然也可以用两张照片，但这样的话就要舍弃掉一个内参了γ=0）
通过至少含一个棋盘格的三幅图像，应用上述公式我们就可以估算出B了。得到B后，我们通过cholesky分解 ，就可以轻松地得到摄像机的内参阵A。
实践2
同实践1，获得三副标定板影像，以及对应得uv，xy坐标以及H矩阵如下：
图片2
uv=[303 553
310 746
315 932
457 541
462 745
470 1137
630 303
632 526
634 743
639 1159
642 1365
644 1562];
xy=[-20 10
-10 10
0 10
-20 0
-10 0
10 0
-30 -10
-20 -10
-10 -10
10 -10
20 -10
30 -10];
H=[ 0.9209 -13.1715 465.9604
20.6899 4.7150 942.7371
0.0011 0.0062 1.0000]
图片3
uv=[266 520
272 741
275 957
279 1170
462 535
467 947
469 1145
635 346
635 745
637 1125];
xy=[-20 20
-10 20
0 20
10 20
-20 10
0 10
10 10
-30 0
-10 0
10 0];
H=[0.6984 -19.5586 636.1907
20.0233 -4.2438 936.6151
0.0010 -0.0055 1.0000]
求解B
函数：
function V=MyFunCreateV(H)
i=1;
j=2;
v12=[H(i,1)*H(j,1)
H(i,1)*H(j,2)+H(i,2)*H(j,1)
H(i,2)*H(j,2)
H(i,3)*H(j,1)+H(i,1)*H(j,3)
H(i,3)*H(j,2)+H(i,2)*H(j,3)
H(i,3)*H(j,3)];
i=1;
j=1;
v11=[H(i,1)*H(j,1)
H(i,1)*H(j,2)+H(i,2)*H(j,1)
H(i,2)*H(j,2)
H(i,3)*H(j,1)+H(i,1)*H(j,3)
H(i,3)*H(j,2)+H(i,2)*H(j,3)
H(i,3)*H(j,3)];
i=2;
j=2;
v22=[H(i,1)*H(j,1)
H(i,1)*H(j,2)+H(i,2)*H(j,1)
H(i,2)*H(j,2)
H(i,3)*H(j,1)+H(i,1)*H(j,3)
H(i,3)*H(j,2)+H(i,2)*H(j,3)
H(i,3)*H(j,3)];
V=[v12'
(v11-v22)'];
% [a,b,c]=svd(V);
% B=a(:,6);
end
数据输入输出
H1=[ -0.6017 -17.1080 552.9464
16.2357 -1.7699 774.8146
-0.0006 -0.0016 1.0000];
H2=[ 0.9209 -13.1715 465.9604
20.6899 4.7150 942.7371
0.0011 0.0062 1.0000];
H3=[0.6984 -19.5586 636.1907
20.0233 -4.2438 936.6151
0.0010 -0.0055 1.0000] ;
V1=MyFunCreateV(H1);
V2=MyFunCreateV(H2);
V3=MyFunCreateV(H3);
V=[V1
V2
V3];
[a,b,c]=svd(V);
B=c(:,6)
b =
0.7102
-0.5751
0.4055
-0.0167
0.0128
0.0004
B =
0.7102 -0.5751 -0.0167
-0.5751 0.4055 0.0128
-0.0167 0.0128 0.0004
理论3
利用B，求出内参矩阵A
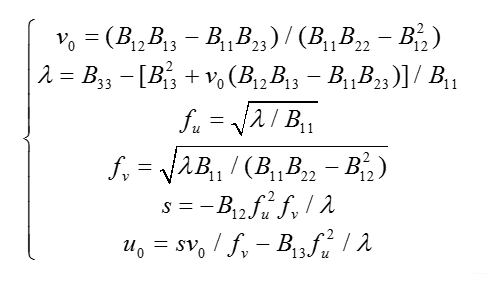
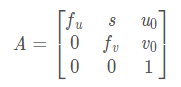
注意：
由于照片数量较少，所以结果可能出现非数字或虚数，但是理论没有问题，增加照片数量即能成功
clear all
clc
H1=MyH('MyPlate1.jpg') ;
H2=MyH('MyPlate2.jpg') ;
H3=MyH('MyPlate3.jpg') ;
H4=MyH('MyPlate4.jpg') ;
H5=MyH('MyPlate5.jpg') ;
H6=MyH('MyPlate6.jpg') ;
H7=MyH('MyPlate7.jpg') ;
H8=MyH('MyPlate8.jpg') ;
H9=MyH('MyPlate9.jpg') ;
H10=MyH('MyPlate10.jpg') ;
H11=MyH('MyPlate11.jpg') ;
H12=MyH('MyPlate12.jpg') ;
H13=MyH('MyPlate13.jpg') ;
H14=MyH('MyPlate14.jpg') ;
H15=MyH('MyPlate15.jpg') ;
H16=MyH('MyPlate16.jpg') ;
V1=MyFunCreateV(H1);
V2=MyFunCreateV(H2);
V3=MyFunCreateV(H3);
V4=MyFunCreateV(H4);
V5=MyFunCreateV(H5);
V6=MyFunCreateV(H6);
V7=MyFunCreateV(H7);
V8=MyFunCreateV(H8);
V9=MyFunCreateV(H9);
V10=MyFunCreateV(H10);
V11=MyFunCreateV(H11);
V12=MyFunCreateV(H12);
V13=MyFunCreateV(H13);
V14=MyFunCreateV(H14);
V15=MyFunCreateV(H15);
V16=MyFunCreateV(H16);
V=[V1
V2
V3
V4
V5
V6
V7
V8
V9
V10
V11
V12
V13
V14
V15
V16];
V=V'*V;
[u, s, v]=svd(V);
%张氏解法
% b=v(:,6)
% B=[b(1,1),b(2,1),b(4,1)
% b(2,1),b(3,1),b(5,1)
% b(4,1),b(5,1),b(6,1)]
% v0=(B(1,2)*B(1,3)-B(1,1)*B(2,3))/(B(1,1)*B(2,2)-B(1,2)*B(1,2));
% ramda=B(3,3)-((B(1,3)*B(1,3)+v0*(B(1,2)*B(1,3)-B(1,1)*B(2,3))))/B(1,1);
% fu=sqrt(ramda/B(1,1));
% fv=sqrt(ramda*B(1,1)/(B(1,1)*B(2,2)-B(1,2)*B(1,2)));
% s=-B(1,2)*fu*fu*fv/ramda;
% u0=s*v0/fv-B(1,3)*fu*fu/ramda;
% A=[fu s u0
% 0 fv v0
% 0 0 1]
% A =
%
% 0.0013 -0.0002 0.0006
% 0 0.0013 0.0009
% 0 0 1.0000
%网上私人解法
b=v(:,6);
v0=(b(2)*b(4)-b(1)*b(5))/(b(1)*b(3)-b(2)^2);
s=b(6)-(b(4)^2+v0*(b(2)*b(4)-b(1)*b(5)))/b(1)
alpha_u=sqrt(s/b(1));
alpha_v=sqrt(s*b(1)/(b(1)*b(3)-b(2)^2));
skewness=-b(2)*alpha_u*alpha_u*alpha_v/s;
u0=skewness*v0/alpha_u-b(4)*alpha_u*alpha_u/s;
A=[alpha_u skewness u0
0 alpha_v v0
0 0 1]
mytest=1
% A =
%
% 0.0013 -0.0002 0.0006
% 0 0.0013 0.0009
% 0 0 1.0000
% A =
%
% 0.0018 -0.0002 0.0008
% 0 0.0017 0.0013
% 0 0 1.0000
% r1=s*inv(A)*H1(:,1);
% r2=s*inv(A)*H1(:,2);
% r3=r1*r2;
% t=s*inv(A)*H1(:,3);
% RL=[r1 r2 r3];
% [u s v]=svd(RL);
% RL=u*v';
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
