hw_0428
clearvars; clc; % hw_0428_tx.m
mesh_N_list=[4;8;16;32;64];
obj = solution(mesh_N_list);
obj.plot();
% solution.m
classdef solution
properties (Access = private)
mesh_N_list
end
methods
function obj = solution(mesh_N_list)
obj.mesh_N_list = mesh_N_list;
end
function plot(obj)
plts = [];
strs = [];
errs = [];
[plt, str] = obj.plot_ext();
plts = [plts; plt];
strs = [strs; str];
for ii = 1:size(obj.mesh_N_list,1)
mesh_N = obj.mesh_N_list(ii,1);
[plt, str, err] = obj.plot_num(mesh_N);
plt.LineStyle = '--';
plt.MarkerEdgeColor = [0,0,0];
plt.LineWidth = 1.0;
plt.Color = [0,0,0,(ii/size(obj.mesh_N_list,1))];
plt.MarkerSize = (1-((ii-1)/size(obj.mesh_N_list,1)))*12;
plts = [plts; plt];
strs = [strs; str];
errs = [errs; err];
end
leg = legend(plts, strs);
leg.FontSize = 17;
leg.Box = 'off';
leg.Location = 'best';
obj.show_order(errs);
saveas(gcf, "./fig1-1.png");
close(gcf);
end
end
methods (Access = private)
function u_num = get_u_num(~, mesh_N)
N=mesh_N;
h=2*pi/N;
a=2*h;
b=1;
c=-1;
B=zeros(N-1,1);
A=diag(a*ones(N-1,1))+diag(b*ones(N-2,1),1)+diag(c*ones(N-2,1),-1);
for i=1:N-1
B(i,1)=(sin(h*i)+cos(h*i))*2*h;
end
u_num = A\B;
u_num = [0;u_num;0];
end
function u_ext = get_ext(~, mesh_N)
u_ext=zeros(mesh_N-1,1);
h=2*pi/mesh_N;
for j=1:mesh_N-1
u_ext(j,1)=sin(h*j);
end
u_ext = [0;u_ext;0];
end
function u_err = get_u_err(obj, u_num, mesh_N)
u_ext = obj.get_ext(mesh_N);
u_err = abs(u_num-u_ext);
u_err = max(u_err); % infty_err
end
function x = get_x(~,mesh_N)
h = 2*pi/mesh_N;
x = 0:h:2*pi;
end
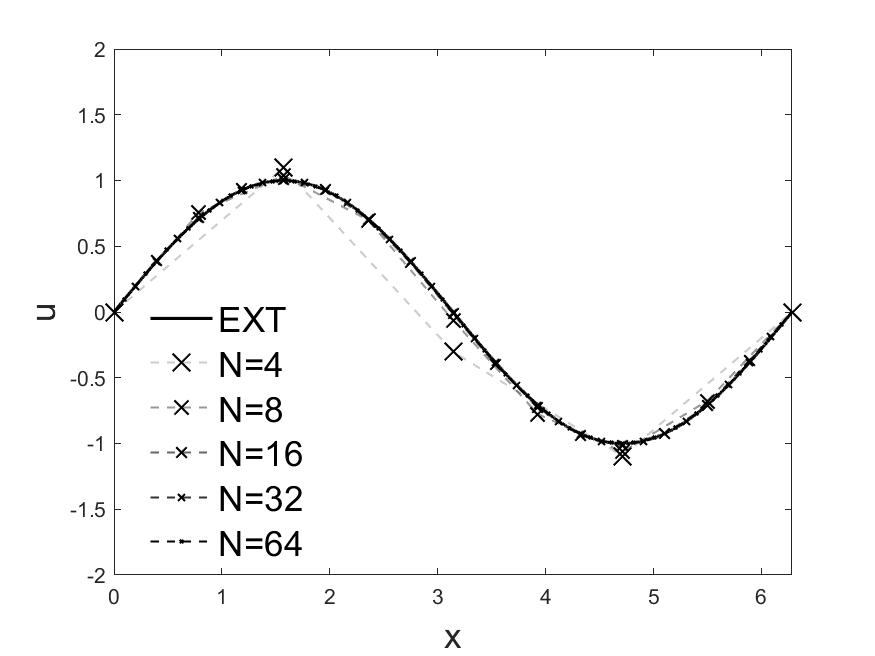
function [plt, str] = plot_ext(~)
fig = figure(1);
x_ext=0:2*pi/10000:2*pi;
y_ext=sin(x_ext);
plt = plot(x_ext,y_ext,'black');
plt.LineWidth = 1.5;
hold on;
xl = xlabel('x');
yl = ylabel('u');
xl.FontSize = 17;
yl.FontSize = 17;
fig.CurrentAxes.XLim = [0,2*pi];
fig.CurrentAxes.YLim = [-2.0,2.0];
str = "EXT";
end
function [plt, str, err] = plot_num(obj,mesh_N)
u_num = obj.get_u_num(mesh_N);
u_err = obj.get_u_err(u_num, mesh_N);
x = obj.get_x(mesh_N);
plt = plot(x,u_num,'x');
str = "N="+num2str(mesh_N);
err = u_err;
end
function show_order(obj, errs)
display("meshN="+num2str(obj.mesh_N_list));
display(errs);
orders = zeros(size(obj.mesh_N_list,1)-1,1);
for ii = 1:(size(obj.mesh_N_list,1)-1)
orders(ii,1) = log(errs(ii+1,1)/errs(ii,1))/...
log(obj.mesh_N_list(ii,1)/obj.mesh_N_list(ii+1,1));
end
disp(orders);
end
end
end
clearvars; clc; % hw_0505_tx.m
Nt=1000;
Nx=100;
obj = solution(Nx, Nt);
obj.plot();
% init.m
classdef init
properties (Access = private)
func;
Nx;
end
methods
function obj = init(func, Nx)
obj.func = func;
obj.Nx = Nx;
end
function init_x = get_init_x(obj)
switch(obj.func)
case 'dis' % 1 - discontinuity
init_x = obj.get_dis();
case 'sin' % 2 - sin
init_x = obj.get_sin();
end
end
end
methods (Access = private)
function init_x = get_dis(obj)
init_x = zeros(obj.Nx+1, 1);
for ii = 1 : (obj.Nx+1)
deltax = 100.0/obj.Nx;
xii = (ii-1)*deltax;
if (xii >= 40) && (xii <= 60)
init_x(ii,1) = 1.0;
else
init_x(ii,1) = 0.0;
end
end
end
function init_x = get_sin(obj)
init_x = zeros(obj.Nx+1, 1);
for ii = 1 : (obj.Nx+1)
deltax = 100/obj.Nx;
xii = (ii-1)*deltax;
init_x(ii,1) = sin(0.02*pi*xii);
end
end
end
end
% solution.m
classdef solution
properties (Access = private)
Nx;
Nt;
func;
end
methods
function obj = solution(Nx, Nt)
obj.Nx = Nx;
obj.Nt = Nt;
end
function plot(obj)
obj.func = 'sin';
obj.plot_sin();
obj.func = 'dis';
obj.plot_dis();
end
end
methods (Access = private)
function final_x = get_upwind1st(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 2 : (obj.Nx+1)
A(ii, jj) = A(ii, jj-1) - uu*deltaT/deltax*...
(A(ii, jj-1)-A(ii-1, jj-1));
% 1st order upwind
end
A(1, jj) = A(obj.Nx+1, jj);
end
final_x = A(:, obj.Nt+1);
end
function xx = get_xx(obj)
deltax = 100.0/obj.Nx;
xx = 0 : deltax : 100;
end
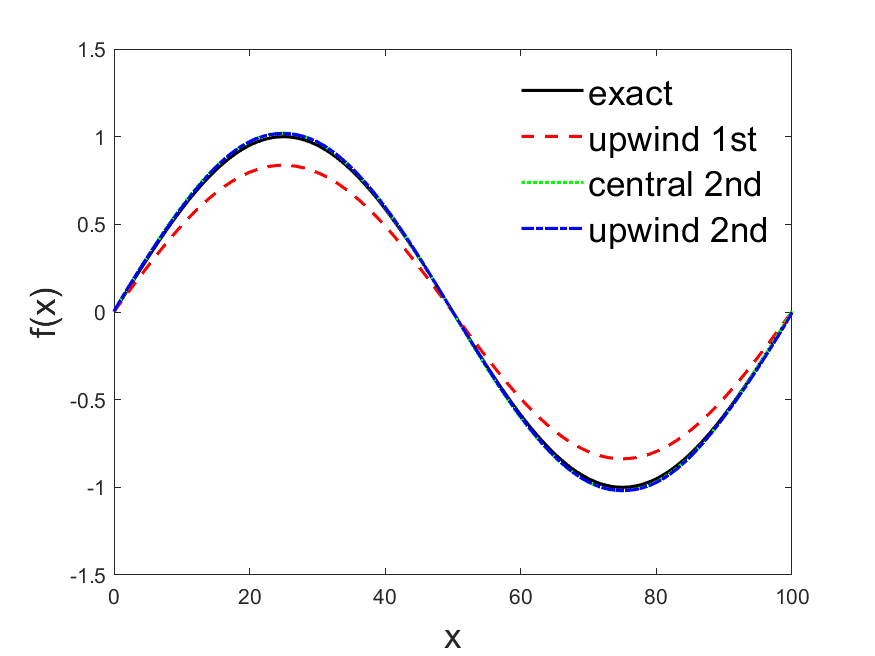
function plot_sin(obj)
func = 'sin';
fig = figure(1);
xx = obj.get_xx();
obj_init = init(func, obj.Nx);
plts = [];
strs = [];
final_x = obj_init.get_init_x();
init_x = obj_init.get_init_x();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Black';
plt.LineWidth = 1.5;
str = "exact";
plts = [plts; plt];
strs = [strs; str];
final_x = obj.get_upwind1st();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Red';
plt.LineStyle = '--';
plt.LineWidth = 1.5;
str = "upwind 1st";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
final_x = obj.get_central2nd();
plt = plot(xx, final_x);
plt.LineStyle = ':';
plt.LineWidth = 1.5;
plt.Color = 'Green';
str = "central 2nd";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
hold on;
final_x = obj.get_upwind2nd();
plt = plot(xx, final_x);
plt.LineStyle = '-.';
plt.Color = 'Blue';
plt.LineWidth = 1.5;
str = "upwind 2nd";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
hold on;
fig.CurrentAxes.XLim = [0, 100];
fig.CurrentAxes.YLim = [-1.5, 1.5];
xl = xlabel("x");
yl = ylabel("f(x)");
xl.FontSize = 17;
yl.FontSize = 17;
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
saveas(gcf, "sin.png");
close(gcf);
end
function final_x = get_central2nd(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 2 : obj.Nx
A(ii, jj) = A(ii, jj-1)-0.5*uu*deltaT/deltax*...
(A(ii+1, jj-1)-A(ii-1, jj-1));
% 2nd order central difference
end
A(1, jj) = A(1, jj-1)-0.5*uu*deltaT/deltax*...
(A(2, jj-1)-A(obj.Nx, jj-1));
A(obj.Nx+1, jj) = A(1, jj);
end
final_x = A(:, obj.Nt+1);
end
function final_x = get_upwind2nd(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 3 : (obj.Nx+1)
A(ii, jj) = A(ii, jj-1)-0.5*uu*deltaT/deltax*...
(3*A(ii, jj-1)-4*A(ii-1, jj-1)+A(ii-2, jj-1));
% 2nd order upwind
end
A(2, jj) = A(2, jj-1)-0.5*uu*deltaT/deltax*...
(3*A(2, jj-1)-4*A(1, jj-1)+A(obj.Nx, jj-1));
A(1, jj) = A(obj.Nx+1, jj-1);
end
final_x = A(:, obj.Nt+1);
len = length(final_x);
mid = (len+1)/2;
for ii = 1 : (mid-1)
switch(obj.func)
case 'dis' % 1 - discontinuity
final_x(len-ii+1, 1) = final_x(ii, 1);
case 'sin' % 2 - sin
final_x(len-ii+1, 1) = - final_x(ii, 1);
end
end
end
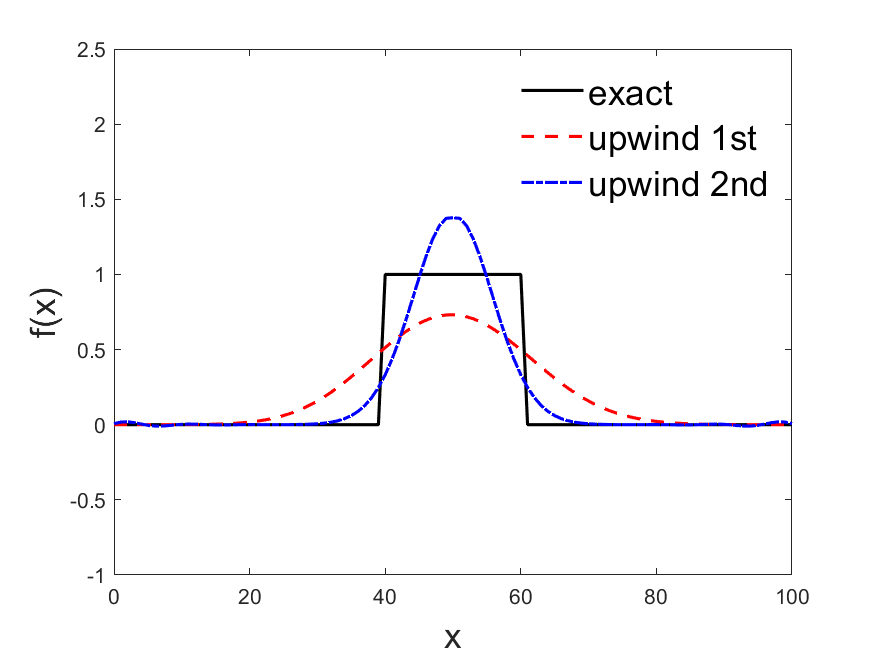
function plot_dis(obj)
fig = figure(1);
xx = obj.get_xx();
obj_init = init(obj.func, obj.Nx);
plts = [];
strs = [];
final_x = obj_init.get_init_x();
init_x = obj_init.get_init_x();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Black';
plt.LineWidth = 1.5;
str = "exact";
plts = [plts; plt];
strs = [strs; str];
final_x = obj.get_upwind1st();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Red';
plt.LineStyle = '--';
plt.LineWidth = 1.5;
str = "upwind 1st";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
final_x = obj.get_central2nd();
str = "central 2nd";
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
hold on;
final_x = obj.get_upwind2nd();
plt = plot(xx, final_x);
plt.LineStyle = '-.';
plt.Color = 'Blue';
plt.LineWidth = 1.5;
str = "upwind 2nd";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
hold on;
fig.CurrentAxes.XLim = [0, 100];
fig.CurrentAxes.YLim = [-1.0, 2.5];
xl = xlabel("x");
yl = ylabel("f(x)");
xl.FontSize = 17;
yl.FontSize = 17;
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
saveas(gcf, "dis.png");
% close(gcf);
end
end
end
clearvars; clc; % hw_0512_tx.m
meshN = 5;
obj = solution(meshN);
obj.solve();
% solution.m
classdef solution
properties (Access = private)
L_ = 1;
rho_ = 1;
gamma_ = 0.1;
u_ = 0.1;
phi0_ = 1;
phi1_ = 0;
A_ = 1;
meshN_;
end
methods
function obj = solution(meshN)
obj.meshN_ = meshN;
end
function solve(obj)
[A,b] = obj.get_Ab_CDS_();
sol_CDS = A \ b;
disp(sol_CDS);
end
end
methods (Access = private)
function [A,b] = get_Ab_CDS_(obj)
F = obj.rho_ * obj.u_ * obj.A_;
D = obj.gamma_ * obj.A_;
aw = 1/2*F*D;
ae = -1/2*F*D;
ap = aw + ae;
diag0 = ones(obj.meshN_-1,1) * ap;
A = diag(diag0);
diag1 = ones(obj.meshN_-2,1)*(-aw);
diag2 = ones(obj.meshN_-2,1)*(-ae);
A = A + diag(diag1,-1) + diag(diag2,1);
b = zeros(obj.meshN_-1, 1);
b(1) = aw * obj.phi0_;
b(end) = ae * obj.phi1_;
end
end
end
import numpy as np
import matplotlib.pyplot as plt
class solution:
def __init__(self, dictionary0):
self.L = dictionary0['L']
self.rho = dictionary0['rho']
self.gamma = dictionary0['gamma']
self.u = dictionary0['u']
self.phi0 = dictionary0['phi0']
self.phiL = dictionary0['phiL']
self.n_mesh = dictionary0['n_mesh']
self.A = 1
def plot(self):
sol1, sol2 = self._get_num()
x, ana = self._get_ana()
fig, ax = plt.subplots()
line1 = ax.plot(x, ana, '-k^', markersize=10, markerfacecolor='none', linewidth=2, markeredgewidth=2)
line2 = ax.plot(x, sol1, '--rx', markersize=10, markerfacecolor='none', linewidth=2, markeredgewidth=2)
line3 = ax.plot(x, sol2, '-.go', markersize=10, markerfacecolor='none', linewidth=2, markeredgewidth=2)
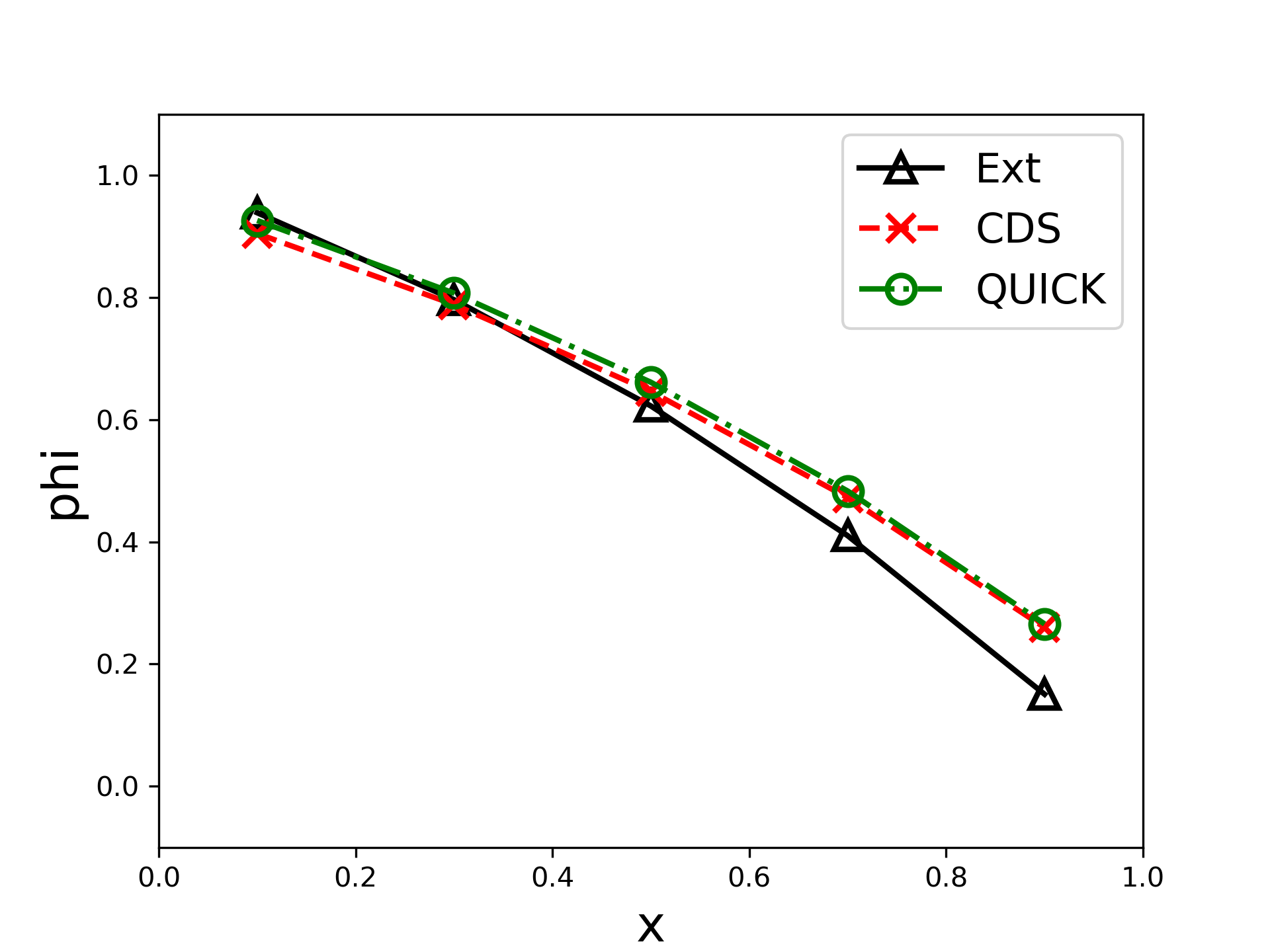
line1[0].set_label("Ext")
line2[0].set_label("CDS")
line3[0].set_label("QUICK")
ax.legend(prop={"size": 15})
ax.set_xlabel("x", fontsize=18)
ax.set_ylabel("phi", fontsize=18)
ax.set_xlim([0.0, 1.0])
ax.set_ylim([-0.1, 1.1])
sol1_diff = np.abs(sol1 - ana)
sol2_diff = np.abs(sol2 - ana)
max1_diff = max([np.max(sol1_diff)])
max2_diff = max([np.max(sol2_diff)])
print("CDS err = ", max1_diff)
print("QUICK err = ", max2_diff)
# plt.show()
plt.savefig('./fig1-1.png', dpi=300)
def _get_num(self):
a1, b1 = self.__get_ab_cds__()
a2, b2 = self.__get_ab_quick__()
sol_cds = np.dot(np.linalg.inv(a1), b1)
sol_quick = np.dot(np.linalg.inv(a2), b2)
return sol_cds, sol_quick
def __get_ab_cds__(self):
dx = self.L / self.n_mesh
f = self.rho * self.u * self.A
d = self.gamma * self.A / dx
aw = 1 / 2 * f + d
ae = - 1 / 2 * f + d
ap = aw + ae
diagonal0 = np.ones(self.n_mesh) * ap
a = np.diag(diagonal0)
diagonal1 = np.ones(self.n_mesh - 1) * (-aw)
diagonal2 = np.ones(self.n_mesh - 1) * (-ae)
a = a + np.diag(diagonal1, k=-1) + np.diag(diagonal2, k=1)
b = np.zeros(self.n_mesh)
b[0] = aw * self.phi0
b[-1] = ae * self.phiL
return a, b
def __get_ab_quick__(self):
dx = self.L / self.n_mesh
f = self.rho * self.u * self.A
d = self.gamma * self.A / dx
aw = 6 / 8 * max(f, 0) - 3 / 8 * max(-f, 0) + 1 / 8 * max(f, 0) + d
aww = -1 / 8 * max(f, 0)
ae = 6 / 8 * max(-f, 0) - 3 / 8 * max(f, 0) + 1 / 8 * max(-f, 0) + d
aee = -1 / 8 * max(-f, 0)
ap = aww + aw + ae + aee
diagnose0 = np.ones(self.n_mesh) * ap
diagnose1 = np.ones(self.n_mesh-2) * (-aee)
diagnose2 = np.ones(self.n_mesh-1) * (-ae)
diagnose3 = np.ones(self.n_mesh-1) * (-aw)
diagnose4 = np.ones(self.n_mesh-2) * (-aww)
a = np.diag(diagnose0) + np.diag(diagnose1, k=2) + np.diag(diagnose2, k=1) + np.diag(diagnose3, k=-1) + \
np.diag(diagnose4, k=-2)
b = np.zeros(self.n_mesh)
b[0] = aw * self.phi0
b[1] = aww * self.phi0
b[-2] = aee * self.phiL
b[-1] = ae * self.phiL
return a, b
def _get_ana(self):
half_len = self.L/(self.n_mesh*2.0)
x = np.linspace(half_len, (self.L-half_len), self.n_mesh)
phi = (np.exp(self.rho * self.u * x / self.gamma) - 1) / (
np.exp(self.rho * self.u * self.L / self.gamma) - 1) * (self.phiL - self.phi0) + self.phi0
return x, phi
if __name__ == '__main__':
dictionary = {
'L': 1,
'rho': 1,
'gamma': 0.1,
'u': 0.1,
'phi0': 1,
'phiL': 0,
'n_mesh': 5
}
s = solution(dictionary0=dictionary)
s.plot()
clearvars; clc; % hw_0519_tx.m
Nt = 10000;
Nx = 100;
obj = solution(Nx, Nt);
obj.plot();
% init.m
classdef init
properties (Access = private)
func;
Nx;
end
methods
function obj = init(func, Nx)
obj.func = func;
obj.Nx = Nx;
end
function init_x = get_init_x(obj)
switch(obj.func)
case 'dis' % 1 - discontinuity
init_x = obj.get_dis();
case 'sin' % 2 - sin
init_x = obj.get_sin();
end
end
end
methods (Access = private)
function init_x = get_dis(obj)
init_x = zeros(obj.Nx+1, 1);
for ii = 1 : (obj.Nx+1)
deltax = 100.0/obj.Nx;
xii = (ii-1)*deltax;
if (xii >= 40) && (xii <= 60)
init_x(ii,1) = 1.0;
else
init_x(ii,1) = 0.0;
end
end
end
function init_x = get_sin(obj)
init_x = zeros(obj.Nx+1, 1);
for ii = 1 : (obj.Nx+1)
deltax = 100/obj.Nx;
xii = (ii-1)*deltax;
init_x(ii,1) = sin(0.02*pi*xii);
end
end
end
end
% solution.m
classdef solution
properties (Access = private)
Nx;
Nt;
func;
end
methods
function obj = solution(Nx, Nt)
obj.Nx = Nx;
obj.Nt = Nt;
end
function plot(obj)
obj.func = 'sin';
obj.plot_sin();
obj.func = 'dis';
obj.plot_dis();
end
end
methods (Access = private)
function final_x = get_upwind1st(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 2 : (obj.Nx+1)
A(ii, jj) = A(ii, jj-1) - uu*deltaT/deltax*...
(A(ii, jj-1)-A(ii-1, jj-1));
% 1st order upwind
end
A(1, jj) = A(obj.Nx+1, jj);
end
final_x = A(:, obj.Nt+1);
end
function xx = get_xx(obj)
deltax = 100.0/obj.Nx;
xx = 0 : deltax : 100;
end
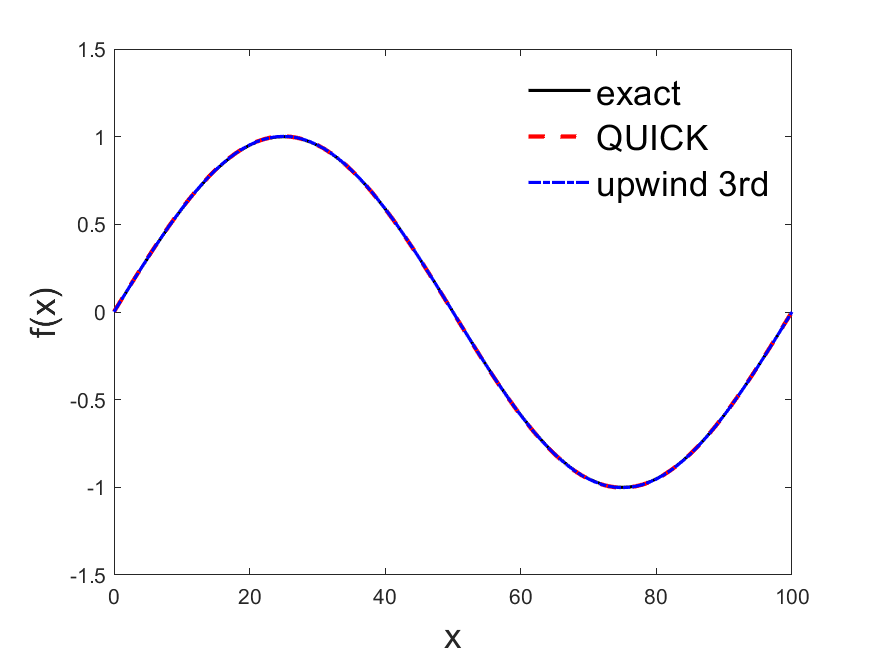
function plot_sin(obj)
obj.func = 'sin';
fig = figure(1);
xx = obj.get_xx();
obj_init = init(obj.func, obj.Nx);
plts = [];
strs = [];
final_x = obj_init.get_init_x();
init_x = obj_init.get_init_x();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Black';
plt.LineWidth = 1.5;
str = "exact";
plts = [plts; plt];
strs = [strs; str];
final_x = obj.get_QUICK();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Red';
plt.LineStyle = '--';
plt.LineWidth = 2.0;
str = "QUICK";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
final_x = obj.get_upwind3rd();
plt = plot(xx, final_x);
plt.LineStyle = '-.';
plt.Color = 'Blue';
plt.LineWidth = 1.5;
str = "upwind 3rd";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
hold on;
fig.CurrentAxes.XLim = [0, 100];
fig.CurrentAxes.YLim = [-1.5, 1.5];
xl = xlabel("x");
yl = ylabel("f(x)");
xl.FontSize = 17;
yl.FontSize = 17;
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
saveas(gcf, "sin.png");
close(gcf);
end
function final_x = get_central2nd(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 2 : obj.Nx
A(ii, jj) = A(ii, jj-1)-0.5*uu*deltaT/deltax*...
(A(ii+1, jj-1)-A(ii-1, jj-1));
% 2nd order central difference
end
A(1, jj) = A(1, jj-1)-0.5*uu*deltaT/deltax*...
(A(2, jj-1)-A(obj.Nx, jj-1));
A(obj.Nx+1, jj) = A(1, jj);
end
final_x = A(:, obj.Nt+1);
end
function final_x = get_upwind2nd(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 3 : (obj.Nx+1)
A(ii, jj) = A(ii, jj-1)-0.5*uu*deltaT/deltax*...
(3*A(ii, jj-1)-4*A(ii-1, jj-1)+A(ii-2, jj-1));
% 2nd order upwind
end
A(2, jj) = A(2, jj-1)-0.5*uu*deltaT/deltax*...
(3*A(2, jj-1)-4*A(1, jj-1)+A(obj.Nx, jj-1));
A(1, jj) = A(obj.Nx+1, jj-1);
end
final_x = A(:, obj.Nt+1);
end
function final_x = get_upwind3rd(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 3 : (obj.Nx)
A(ii, jj) = A(ii, jj-1)-(1/6.0)*uu*deltaT/deltax*...
(2*A(ii+1, jj-1)+3*A(ii, jj-1)-6*A(ii-1, jj-1)+A(ii-2, jj-1));
% 3rd order upwind
end
A(obj.Nx+1, jj) = A(obj.Nx+1, jj-1)-(1/6.0)*uu*deltaT/deltax*...
(2*A(2, jj-1)+3*A(obj.Nx+1, jj-1)-6*A(obj.Nx, jj-1)...
+A(obj.Nx-1, jj-1));
A(2, jj) = A(2, jj-1)-(1/6.0)*uu*deltaT/deltax*...
(2*A(3, jj-1)+3*A(2, jj-1)-6*A(1, jj-1)+A(obj.Nx, jj-1));
A(1, jj) = A(obj.Nx+1, jj-1);
end
final_x = A(:, obj.Nt+1);
end
function final_x = get_QUICK(obj)
uu = 1;
obj_init = init(obj.func, obj.Nx);
init_x = obj_init.get_init_x();
A = zeros(obj.Nx+1, obj.Nt+1);
A(:,1) = init_x;
deltaT = 100.0/obj.Nt;
deltax = 100.0/obj.Nx;
for jj = 2 : (obj.Nt+1)
for ii = 3 : (obj.Nx)
A(ii, jj) = A(ii, jj-1)-(1/8.0)*uu*deltaT/deltax*...
(3*A(ii+1, jj-1)+3*A(ii, jj-1)-7*A(ii-1, jj-1)+A(ii-2, jj-1));
% QUICK
end
A(obj.Nx+1, jj) = A(obj.Nx+1, jj-1)-(1/8.0)*uu*deltaT/deltax*...
(3*A(2, jj-1)+3*A(obj.Nx+1, jj-1)-7*A(obj.Nx, jj-1)...
+A(obj.Nx-1, jj-1));
A(2, jj) = A(2, jj-1)-(1/8.0)*uu*deltaT/deltax*...
(3*A(3, jj-1)+3*A(2, jj-1)-7*A(1, jj-1)+A(obj.Nx, jj-1));
A(1, jj) = A(obj.Nx+1, jj-1);
end
final_x = A(:, obj.Nt+1);
% final_x = A(:, 100);
end
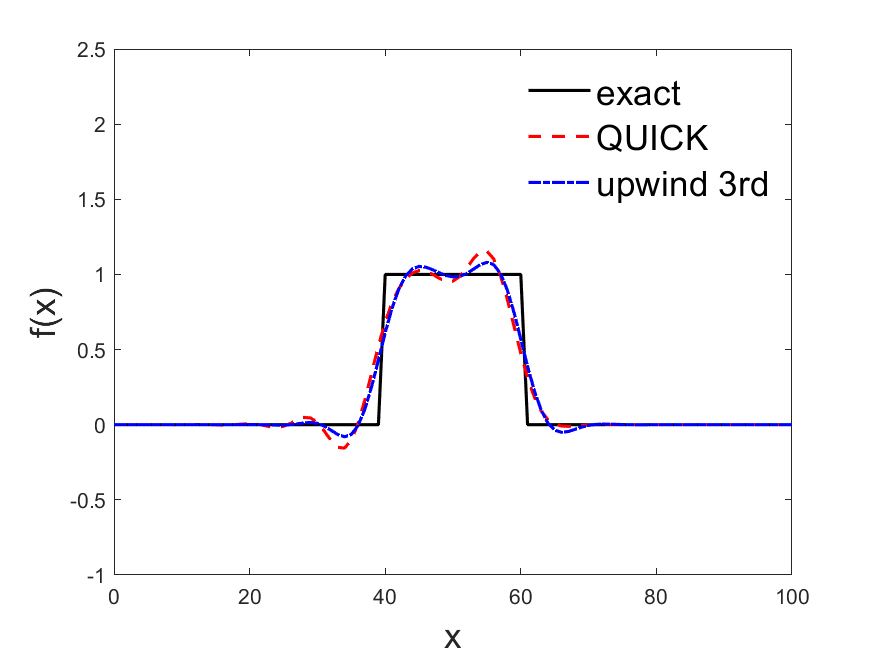
function plot_dis(obj)
fig = figure(2);
xx = obj.get_xx();
obj_init = init(obj.func, obj.Nx);
plts = [];
strs = [];
final_x = obj_init.get_init_x();
init_x = obj_init.get_init_x();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Black';
plt.LineWidth = 1.5;
str = "exact";
plts = [plts; plt];
strs = [strs; str];
final_x = obj.get_QUICK();
plt = plot(xx, final_x);
hold on;
plt.Color = 'Red';
plt.LineStyle = '--';
plt.LineWidth = 1.5;
str = "QUICK";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
final_x = obj.get_central2nd();
str = "central 2nd";
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
hold on;
final_x = obj.get_upwind3rd();
plt = plot(xx, final_x);
plt.LineStyle = '-.';
plt.Color = 'Blue';
plt.LineWidth = 1.5;
str = "upwind 3rd";
plts = [plts; plt];
strs = [strs; str];
x_err = abs(final_x - init_x);
x_err = max(x_err);
disp(str + " err = " + x_err);
hold on;
fig.CurrentAxes.XLim = [0, 100];
fig.CurrentAxes.YLim = [-1.0, 2.5];
xl = xlabel("x");
yl = ylabel("f(x)");
xl.FontSize = 17;
yl.FontSize = 17;
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
saveas(gcf, "dis.png");
close(gcf);
end
end
end
clearvars; clc; % hw_0526_tx.m
meshN = 128;
iterN = 100;
obj = solution(meshN, iterN);
obj.solve();
% solution.m
classdef solution
properties (Access = private)
meshN;
iterN;
end
methods
function obj = solution(meshN, iterN)
obj.meshN = meshN;
obj.iterN = iterN;
end
function solve(obj)
objMesh = mesh(obj.meshN);
func = obj.get_func();
hh = objMesh.get_hh();
phiExt = obj.get_phiExt();
objGaussSeidel = gaussSeidel(obj.iterN, func, hh);
errsGaussSeidel = objGaussSeidel.get_errs(phiExt);
objMultiGrid = multiGrid(obj.iterN, func, hh);
errsMultiGrid = objMultiGrid.get_errs(phiExt);
fig = figure(1);
plts = [];
strs = [];
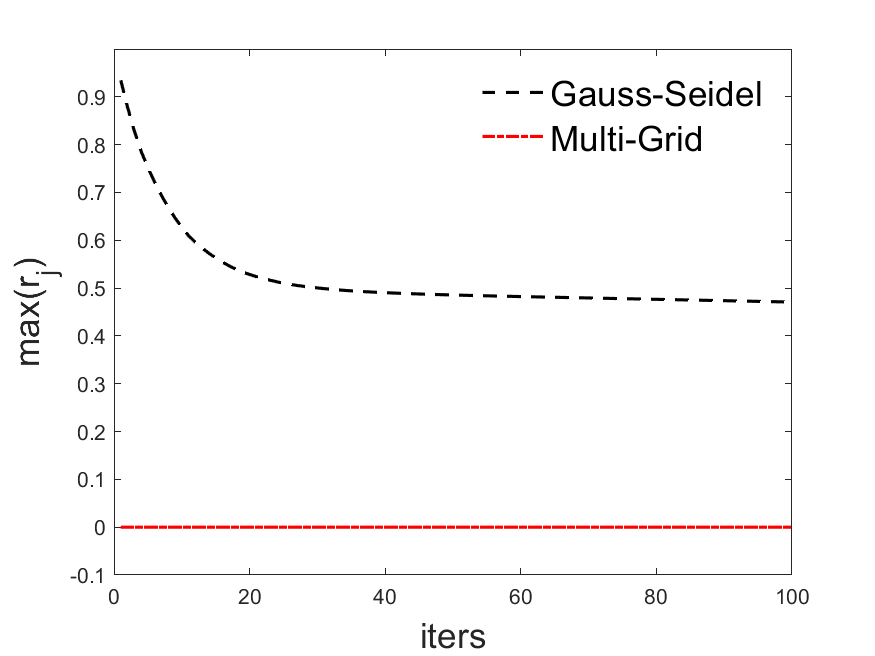
plt = plot(errsGaussSeidel);
plt.Color = "Black";
plt.LineWidth = 1.5;
plt.LineStyle = '--';
str = "Gauss-Seidel";
plts = [plts, plt];
strs = [strs, str];
hold on;
plt = plot(errsMultiGrid);
plt.Color = "Red";
plt.LineWidth = 1.5;
plt.LineStyle = '-.';
str = "Multi-Grid";
plts = [plts, plt];
strs = [strs, str];
hold on;
fig.CurrentAxes.YLim = [-0.1, 1.0];
xl = xlabel("iters");
xl.FontSize = 17;
yl = ylabel("max(r_j)");
yl.FontSize = 17;
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
ld.Location = "Best";
saveas(fig, "./fig1-1.png");
close(fig);
end
end
methods (Access = private)
function func = get_func(obj)
N = obj.meshN;
objMesh = mesh(obj.meshN);
hh = objMesh.get_hh();
func = (sin(pi*[0:N]*hh)+sin(16*pi*[0:N]*hh))/2.0;
end
function phiExt = get_phiExt(obj)
objMesh = mesh(obj.meshN);
xx = objMesh.get_xx();
phiExt = zeros(1, size(xx, 2));
for ii = 1 : size(phiExt, 2)
phiExt(1, ii) = xx2phi(xx(1, ii));
end
function phi = xx2phi(xx)
phi_1 = -(1.0/(2.0*pi^2))*sin(pi*xx);
phi_2 = -(1.0/(2.0*(16.0*pi)^2))*sin(16.0*pi*xx);
phi = phi_1 + phi_2;
end
end
end
end
% mesh.m
classdef mesh
properties (Access = private)
meshN;
end
methods
function obj = mesh(meshN)
obj.meshN = meshN;
end
function xx = get_xx(obj)
N = obj.meshN;
L = 1.0;
hh = L/N;
xx = 0.0:hh:1.0;
end
function hh = get_hh(obj)
N = obj.meshN;
L = 1.0;
hh = L/N;
end
end
end
% gaussSeidel.m
classdef gaussSeidel
properties (Access = private)
iterN_;
func_;
hh_;
end
methods
function obj = gaussSeidel(iterN, func, hh)
obj.iterN_ = iterN;
obj.func_ = func;
obj.hh_ = hh;
end
function errs = get_errs(obj, phiExt)
maxiter = obj.iterN_;
func = obj.func_;
NN = size(func, 2)-1;
hh = obj.hh_;
phiNum = zeros(1, size(func, 2));
errs = zeros(1, maxiter);
for ii = 1 : maxiter
for jj = 2 : NN
phiNum(1, jj) = (phiNum(1, jj-1)+...
phiNum(1, jj+1))/2.0...
-(hh^2/2.0)*func(1, jj);
end
errList = abs(phiNum - phiExt);
errs(1, ii) = max(errList);
errList = residual(phiNum, func, hh);
errs(1, ii) = max(errList);
end
function res = residual(phi,f,h)
N = length(phi)-1;
res = zeros(1,N+1);
res(2:N) = f(2:N)-(phi(1:N-1)-2*phi(2:N)+phi(3:N+1))/h^2;
end
end
end
end
% multiGrid.m
classdef multiGrid
properties (Access = private)
iterN_;
func_;
hh_;
end
methods
function obj = multiGrid(iterN, func, hh)
obj.iterN_ = iterN;
obj.func_ = func;
obj.hh_ = hh;
end
function errs = get_errs(obj, phiExt)
maxiter = obj.iterN_;
errs = zeros(1, maxiter);
hh = obj.hh_;
func = obj.func_;
phiNum = zeros(1, size(func, 2));
for cnt = 1 : maxiter
phiNum = V_Cycle(phiNum, func, hh);
errList = abs(phiNum - phiExt);
errs(1, cnt) = max(errList);
% errList = residual(phiNum, func, hh);
% errs(1, cnt) = max(errList);
end
function phi = V_Cycle(phi,f,h)
% Recursive V-Cycle Multigrid for solving
% the Poisson equation (nabla^2 phi = f)
% on a uniform grid of spacing h
% Pre-Smoothing
phi = smoothing(phi,f,h);
% Compute Residual Errors
r = residual(phi,f,h);
% Restriction
rhs = restriction(r);
eps = zeros(size(rhs));
% stop recursion at smallest grid size, otherwise continue recursion
if length(eps)-1 == 2
eps = smoothing(eps,rhs,2*h);
else
eps = V_Cycle(eps,rhs,2*h);
end
% Prolongation and Correction
phi = phi + prolongation(eps);
% Post-Smoothing
phi = smoothing(phi,f,h);
end
function res = smoothing(phi,f,h)
N = length(phi)-1;
x0 = zeros(N+1,1);
diag0 = ones(1,N+1)*(-2);
diag1 = ones(1,N);
A = diag(diag0) + diag(diag1,-1) + diag(diag1,1);
A(1,1) = 1;
A(1,2) = 0;
A(end,end) = 1;
A(end,end-1) = 0;
b = zeros(N+1,1);
b(1) = 0;
b(end) = 0;
b(2:end-1) = h^2 * f(2:end-1);
r0 = A*x0 - b;
p0 = -r0;
for i = 1 : 2
alpha = (r0' * r0) / (p0' * A * p0);
x = x0 + alpha * p0;
r = r0 + alpha * A * p0;
beta = (r' * r) /(r0' * r0);
p = -r + beta * p0;
if norm(x - x0) <= 10^(-8)
break;
end
x0 = x;
r0 = r;
p0 = p;
end
res = x0';
end
function res = residual(phi,f,h)
N = length(phi)-1;
res = zeros(1,N+1);
res(2:N) = f(2:N)-(phi(1:N-1)-2*phi(2:N)+phi(3:N+1))/h^2;
end
function res = restriction(r)
N = (length(r)-1)/2;
res = zeros(1,N+1);
for j = 2:N
res(j) = (r(2*j-2)+2*r(2*j-1)+r(2*j))/4;
end
end
function res = prolongation(eps)
N = (length(eps)-1)*2;
res = zeros(1,N+1);
for j = 2:2:N
res(j) = (eps(j/2)+eps(j/2+1))/2;
end
for j = 1:2:N+1
res(j) = eps((j+1)/2);
end
end
end
end
end
Gauss-Seidel_xb.py
import numpy as np
import matplotlib.pyplot as plt
N = 64
L = 1
dx = L / N
phi = np.zeros(shape=(N + 1,))
new = np.zeros(shape=(N + 1,))
tmp = np.array([np.sin(np.pi * i * dx) / 2 + np.sin(16 * np.pi * i * dx) / 2 for i in range(1, N)])
r0 = np.zeros(shape=(N + 1,))
r10 = np.zeros(shape=(N + 1,))
r100 = np.zeros(shape=(N + 1,))
r0[1:N] = tmp
resi = [0]
resi[0] = np.max(np.abs(tmp))
for t in range(0, 10000):
for j in range(1, N):
new[j] = (phi[j + 1] + new[j - 1] - dx ** 2 * tmp[j - 1]) / 2
new[0] = 0
new[N] = 0
r = tmp - (new[0:N - 1] - 2 * new[1:N] + new[2:N + 1]) / dx ** 2
resi.append(np.max(np.abs(r)))
phi = new
if t == 10:
r10[1:N] = r
elif t == 100:
r100[1:N] = r
if(resi[-1] < 0.001):
print("converge at {} iterations".format(t))
break
plt.figure()
plt.plot(range(len(resi)), resi, '+-')
plt.xlabel("Number of iterations")
plt.ylabel("max(|r_j|)")
plt.title("Convergence Curve")
plt.figure()
x = np.linspace(0, 1, N + 1)
plt.plot(x, r0, '-', x, r10, '+-', x, r100, 'x-')
plt.legend(['0 iterations','10 iterations','100 iterations'])
plt.xlabel('x_j')
plt.ylabel('r_j')
plt.title('r_j against x_j')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
def smoothing(phi, f, h):
N = np.size(phi) - 1
res = np.zeros(shape=(N + 1,))
for j in range(1, N):
res[j] = (phi[j + 1] + res[j - 1] - h ** 2 * f[j]) / 2
return res
def residual(phi, f, h):
N = np.size(phi) - 1
res = np.zeros(shape=(N + 1,))
res[1:N] = f[1:N] - (phi[0:N - 1] - 2 * phi[1:N] + phi[2:N + 1]) / h ** 2
return res
def restriction(r):
N = int((np.size(r) - 1) / 2)
res = np.zeros(shape=(N + 1,))
for j in range(2, N + 1):
res[j - 1] = (r[2 * j - 3] + 2 * r[2 * j - 2] + r[2 * j - 1]) / 4
return res
def prolongation(eps):
N = (np.size(eps) - 1) * 2
res = np.zeros(shape=(N + 1,))
for j in range(2, N + 1, 2):
res[j - 1] = (eps[int(j / 2 - 1)] + eps[int(j / 2)]) / 2
for j in range(1, N + 2, 2):
res[j - 1] = eps[int((j + 1) / 2 - 1)]
return res
def V_Cycle(phi, f, h):
phi = smoothing(phi, f, h)
r = residual(phi, f, h)
rhs = restriction(r)
eps = np.zeros(np.size(rhs))
if np.size(eps) - 1 == 2:
eps = smoothing(eps, rhs, 2 * h)
else:
eps = V_Cycle(eps, rhs, 2 * h)
phi = phi + prolongation(eps)
phi = smoothing(phi, f, h)
return phi
N = 64
L = 1
h = L / N
phi = np.zeros(shape=(N + 1,))
new = np.zeros(shape=(N + 1,))
f = np.array([np.sin(np.pi * i * h) / 2 + np.sin(16 * np.pi * i * h) / 2 for i in range(0, N + 1)])
resi = []
for cnt in range(0, 1000):
phi = V_Cycle(phi, f, h)
r = residual(phi, f, h)
resi.append(np.max(np.abs(r)))
if (resi[-1] < 0.001):
break
plt.figure()
plt.plot(np.arange(len(resi))*10,resi,'+-')
plt.xlabel('Number of Iterations')
plt.ylabel('max(|r_j|)')
plt.title('Convergence Curve')
plt.show()
clearvars; clc; % multi_grid_zmx.m
N = 64; L = 1;
h = L/N;
phi_multi = zeros(1,N+1);
phi_gauss = zeros(1,N+1);
xx = 0.0:1/N:1.0;
func = (sin(pi*[0:N]*h)+sin(16*pi*[0:N]*h))/2;
for cnt = 1 : 1000
phi_multi = V_Cycle(phi_multi, func, h);
r = residual(phi_multi, func, h);
resi = max(abs(r));
if max(abs(r)) < 0.001
break
end
end
phi_ext = zeros(1, size(xx, 2));
for ii = 1 : size(phi_ext, 2)
phi_ext(1, ii) = xx2phi(xx(1, ii));
end
maxiter = 10000;
tol = 1e-6;
err = Inf;
iter = 0;
while err > tol && iter < maxiter
iter = iter + 1;
oldphi = phi_gauss;
for ii = 2 : N
phi_gauss(ii) = (phi_gauss(ii-1)+phi_gauss(ii+1))/2 - h^2/2*func(ii);
end
err = norm(phi_gauss-oldphi)/norm(oldphi);
end
plot(xx, phi_multi, xx, phi_ext, xx, phi_gauss);
function phi = xx2phi(xx)
phi_1 = -(1.0/(2.0*pi^2))*sin(pi*xx);
phi_2 = -(1.0/(2.0*(16.0*pi)^2))*sin(16.0*pi*xx);
phi = phi_1 + phi_2;
end
function phi = V_Cycle(phi,f,h)
% Recursive V-Cycle Multigrid for solving
% the Poisson equation (nabla^2 phi = f)
% on a uniform grid of spacing h
% Pre-Smoothing
phi = smoothing(phi,f,h);
% Compute Residual Errors
r = residual(phi,f,h);
% Restriction
rhs = restriction(r);
eps = zeros(size(rhs));
% stop recursion at smallest grid size, otherwise continue recursion
if length(eps)-1 == 2
eps = smoothing(eps,rhs,2*h);
else
eps = V_Cycle(eps,rhs,2*h);
end
% Prolongation and Correction
phi = phi + prolongation(eps);
% Post-Smoothing
phi = smoothing(phi,f,h);
end
function res = smoothing(phi,f,h)
N = length(phi)-1;
x0 = zeros(N+1,1);
diag0 = ones(1,N+1)*(-2);
diag1 = ones(1,N);
A = diag(diag0) + diag(diag1,-1) + diag(diag1,1);
A(1,1) = 1;
A(1,2) = 0;
A(end,end) = 1;
A(end,end-1) = 0;
b = zeros(N+1,1);
b(1) = 0;
b(end) = 0;
b(2:end-1) = h^2 * f(2:end-1);
r0 = A*x0 - b;
p0 = -r0;
for i = 1 : 2
alpha = (r0' * r0) / (p0' * A * p0);
x = x0 + alpha * p0;
r = r0 + alpha * A * p0;
beta = (r' * r) /(r0' * r0);
p = -r + beta * p0;
if norm(x - x0) <= 10^(-8)
break;
end
x0 = x;
r0 = r;
p0 = p;
end
res = x0';
end
function res = residual(phi,f,h)
N = length(phi)-1;
res = zeros(1,N+1);
res(2:N) = f(2:N)-(phi(1:N-1)-2*phi(2:N)+phi(3:N+1))/h^2;
end
function res = restriction(r)
N = (length(r)-1)/2;
res = zeros(1,N+1);
for j = 2:N
res(j) = (r(2*j-2)+2*r(2*j-1)+r(2*j))/4;
end
end
function res = prolongation(eps)
N = (length(eps)-1)*2;
res = zeros(1,N+1);
for j = 2:2:N
res(j) = (eps(j/2)+eps(j/2+1))/2;
end
for j = 1:2:N+1
res(j) = eps((j+1)/2);
end
end
hw_prj
clearvars; clc; % main.m
obj = solution();
obj.solve();
% solution.m
classdef solution
properties (Access = private)
t_yNum;
end
methods
function obj = solution()
dataPath = ".\data";
obj.t_yNum = importdata(dataPath+"\t_yNum_3");
end
function solve(obj)
fig = figure(1);
plts = [];
strs = [];
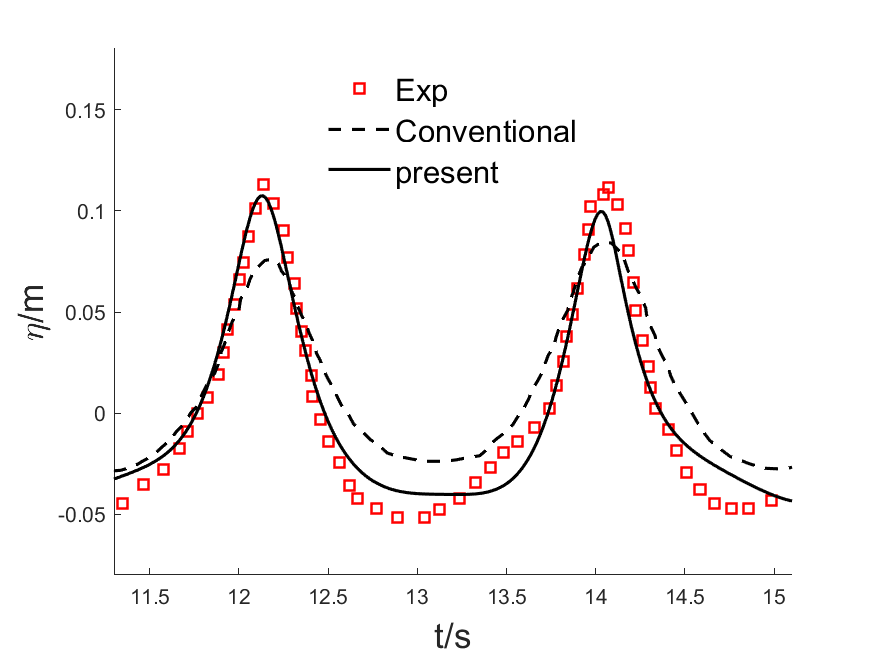
objExp = oeExp();
[plt, str] = objExp.plot();
plts = [plts; plt];
strs = [strs; str];
objConv = oeConv();
[plt, str] = objConv.plot();
plts = [plts; plt];
strs = [strs; str];
x = obj.t_yNum(:, 1);
y = obj.t_yNum(:, 2);
y = process_func1(y);
plt = plot(x, y);
hold on;
plt.LineWidth = 1.5;
plt.Color = 'Black';
str = "present";
fig.CurrentAxes.XLim = [11.3, 15.1];
fig.CurrentAxes.YLim = [-0.08, 0.18];
plts = [plts; plt];
strs = [strs; str];
ld = legend(plts, strs);
ld.FontSize = 15;
ld.Box = 'off';
ld.Location = "North";
xl = xlabel("t/s");
xl.FontSize = 17;
yl = ylabel("\eta/m");
yl.FontSize = 17;
saveas(fig, './t_eta_1.png');
close(fig);
function y_out = process_func1(y_in)
y_out = zeros(size(y_in, 1), 1);
for ii = 1 : size(y_out, 1)
y_out(ii, 1) = y_in(ii, 1) - y_in(1, 1);
end
end
end
end
end
% oeConv.m
classdef oeConv
properties (Access = private)
t_yNum;
end
methods
function obj = oeConv()
dataPath = ".\data";
obj.t_yNum = importdata(dataPath+"\t_yConv.csv");
end
function [plt, str] = plot(obj)
obj = obj.process_data();
x = obj.t_yNum(:, 1);
y = obj.t_yNum(:, 2);
plt = plot(x, y);
hold on;
plt.LineStyle = '--';
plt.LineWidth = 1.5;
plt.Color = "Black";
str = "Conventional";
end
end
methods (Access = private)
function obj = process_data(obj)
x_offSet = 0.15;
x = obj.t_yNum(:, 1);
y = obj.t_yNum(:, 2);
x_new = zeros(size(x, 1), 1);
for ii = 1 : size(x_new, 1)
x_new(ii, 1) = x(ii, 1) + x_offSet;
end
obj.t_yNum = [x_new, y];
end
end
end
% oeExp.m
classdef oeExp
properties (Access = private)
t_yNum;
end
methods
function obj = oeExp()
dataPath = ".\data";
obj.t_yNum = importdata(dataPath+"\t_yExp.csv");
end
function [plt, str] = plot(obj)
obj = obj.process_data();
x = obj.t_yNum(:, 1);
y = obj.t_yNum(:, 2);
plt = scatter(x, y);
hold on;
plt.Marker = 's';
plt.LineWidth = 1.2;
plt.MarkerEdgeColor = "Red";
str = "Exp";
end
end
methods (Access = private)
function obj = process_data(obj)
x_offSet = 0.15;
x = obj.t_yNum(:, 1);
y = obj.t_yNum(:, 2);
x_new = zeros(size(x, 1), 1);
for ii = 1 : size(x_new, 1)
x_new(ii, 1) = x(ii, 1) + x_offSet;
end
obj.t_yNum = [x_new, y];
end
end
end
waveMaker.H
/*---------------------------------------------------------------------------*\
========= |
\\ / F ield | OpenFOAM: The Open Source CFD Toolbox
\\ / O peration |
\\ / A nd | www.openfoam.com
\\/ M anipulation |
\*---------------------------------------------------------------------------*/
#ifndef vofCwaveMakerBCs_H
#define vofCwaveMakerBCs_H
class vofWaveModel
{
public:
// Constructor
vofWaveModel(const fvMesh & mesh);
// Destructor
~vofWaveModel() {}
// public member functions
void updateWaves
(
volVectorField & U,
volScalarField & alpha1,
surfaceScalarField & phi
) const;
//- No copy construct
vofWaveModel(const vofWaveModel&) = delete;
//- No copy assignment
void operator=(const vofWaveModel&) = delete;
private:
// private data
const fvMesh & mesh_;
// basic wave parameters
scalar waveHeight_;
scalar wavePeriod_;
scalar waterDepth_;
scalar waterSurface_;
// wave relaxation zone
scalar waveInputRegion0_;
scalar waveInputRegion1_;
scalar waveOutputRegion0_;
scalar waveOutputRegion1_;
// wave type
string vofWaveType_;
// default parameters
scalar relaxationFactor_ = 3.50;
};
void vofWaveModel::calc_relaxationCoeff_() const
{
using Foam::exp;
using Foam::pow;
scalarList & relaxationCoeff = relaxationCoeffPtr_.ref();
forAll(mesh.C(), cellI)
{
relaxationCoeff[cellI] = 1.0;
scalar xx = mesh.C()[cellI].x();
if(xx>=waveInputRegion0 && xx<=waveInputRegion1)
{
relaxationCoeff[cellI] = 1.0-(exp(pow((waveInputRegion1-xx)/
(waveInputRegion1-waveInputRegion0), relaxationFactor))-1.0)/(exp(1.0)-1.0);
// waveInlet region
}
else if(xx>=waveOutputRegion0 && xx<=waveOutputRegion1)
{
relaxationCoeff[cellI] = 1.0-(exp(pow((xx-waveOutputRegion0)/
(waveOutputRegion1-waveOutputRegion0), relaxationFactor))-1.0)/(exp(1.0)-1.0);
// waveOutlet region
}
}
}
void vofWaveModel::updateWaveBCs_
(
volVectorField & U,
volScalarField & alpha1
) const
{
// Update wave boundary --> Velocity
forAll(mesh.boundary()[patchID],cellI)
{
scalar xx = mesh.boundary()[patchID].Cf()[cellI].x();
scalar yy = mesh.boundary()[patchID].Cf()[cellI].y();
scalar TT = runTime.value();
scalar waveNumber = this -> waveNumber_();
scalar waveOmega = this -> waveOmega_();
scalar theta00 = waveNumber*xx-waveOmega*TT+M_PI/2.0;
scalar waveSurface = this -> waveSurface_(theta00);
scalar waterSurface = this -> waterSurface_;
scalar theoryWaveAlpha1 = 0.0;
vector theoryWaveU = vector::zero;
if(yy <= (waterSurface+waveSurface))
{
theoryWaveAlpha1 = 1.0;
theoryWaveU = this -> theoryWaveU_(theta00, yy);
}
U.boundaryFieldRef()[patchID][cellI] = theoryWaveU;
alpha1.boundaryFieldRef()[patchID][cellI] = theoryWaveAlpha1;
}
}
scalar vofWaveModel::waveSurface_
(
const scalar& theta00
) const
{
// stokes I
using Foam::cos;
scalar waveSurface = 0.0;
if(vofWaveType.compare(stokesIvofWaveType) == 0)
{
scalar waveHeight = this -> waveHeight_;
waveSurface = (waveHeight/2.0)*cos(theta00);
}
else if(vofWaveType.compare(stokesVvofWaveType) == 0)
{
waveSurface =
(
lambda21*Foam::cos(1.0*theta00)
+lambda22*Foam::cos(2.0*theta00)
+lambda23*Foam::cos(3.0*theta00)
+lambda24*Foam::cos(4.0*theta00)
+lambda25*Foam::cos(5.0*theta00)
)/waveNumber;
}
else
{
Info<<"ERROR : vofWaveType no match !! \n";
}
return waveSurface;
}
vector vofWaveModel::theoryWaveU_
(
const scalar& theta00,
const scalar& yy
) const
{
vector theoryWaveU = vector::zero;
if(vofWaveType.compare(stokesIvofWaveType) == 0)
{
theoryWaveU[0] = (waveHeight/2.0)*waveOmega
*cosh(waveNumber*(yy+waterDepth))
/sinh(waveNumber*waterDepth)*cos(theta00);
theoryWaveU[1] = (waveHeight/2.0)*waveOmega
*sinh(waveNumber*(yy+waterDepth))
/sinh(waveNumber*waterDepth)*sin(theta00);
theoryWaveU[2] = 0.0;
}
else if(vofWaveType.compare(stokesVvofWaveType) == 0)
{
theoryWaveU[0] = waveSpeed*
(
1.0*lambda11*cosh(1.0*waveNumber*(yy+waterDepth))*cos(1.0*theta00)
+2.0*lambda12*cosh(2.0*waveNumber*(yy+waterDepth))*cos(2.0*theta00)
+3.0*lambda13*cosh(3.0*waveNumber*(yy+waterDepth))*cos(3.0*theta00)
+4.0*lambda14*cosh(4.0*waveNumber*(yy+waterDepth))*cos(4.0*theta00)
+5.0*lambda15*cosh(5.0*waveNumber*(yy+waterDepth))*cos(5.0*theta00)
) - caliU;
theoryWaveU[1] = waveSpeed*
(
1.0*lambda11*sinh(1.0*waveNumber*(yy+waterDepth))*sin(1.0*theta00)
+2.0*lambda12*sinh(2.0*waveNumber*(yy+waterDepth))*sin(2.0*theta00)
+3.0*lambda13*sinh(3.0*waveNumber*(yy+waterDepth))*sin(3.0*theta00)
+4.0*lambda14*sinh(4.0*waveNumber*(yy+waterDepth))*sin(4.0*theta00)
+5.0*lambda15*sinh(5.0*waveNumber*(yy+waterDepth))*sin(5.0*theta00)
);
theoryWaveU[2] = 0.0;
}
else
{
Info<<"ERROR : vofWaveType no match !! \n";
}
return theoryWaveU;
}
void vofWaveModel::updateWaveZones_
(
volVectorField & U,
volScalarField & alpha1
) const
{
forAll(mesh.C(), cellI)
{
scalar xx = mesh.C()[cellI].x();
scalar TT = runTime.value();
// ------Wave input region------
scalar waveInputRegion0 = this -> waveInputRegion0_;
scalar waveInputRegion1 = this -> waveInputRegion1_;
if((xx >= waveInputRegion0)&&(xx <= waveInputRegion1))
{
scalar waveSpeed = this -> get_waveSpeed_();
scalar distance = waveSpeed*TT;
if((xx - waveInputRegion0) <= distance)
{
scalar waterSurface = this -> waterSurface_;
scalar waveNumber = this -> waveNumber_();
scalar waveOmega = this -> waveOmega_();
scalar theta00 = waveNumber*xx-waveOmega*TT+M_PI/2.0;
scalar theoryWaveAlpha1 = 0.0;
vector theoryWaveU = vector::zero;
scalar waveSurface = this -> waveSurface_(theta00);
scalar yy = mesh.C()[cellI].y();
if(yy <= (waterSurface+waveSurface))
{
theoryWaveAlpha1 = 1.0;
theoryWaveU = this -> theoryWaveU_(theta00, yy);
}
const scalarList & relaxationCoeff = this -> relaxationCoeff_();
scalar oldAlpha1 = alpha1[cellI];
scalar newAlpha1 = relaxationCoeff[cellI]*oldAlpha1 + (1.0-relaxationCoeff[cellI])*theoryWaveAlpha1;
alpha1[cellI] = newAlpha1;
vector oldU = U[cellI];
vector newU = relaxationCoeff[cellI]*oldU + (1.0-relaxationCoeff[cellI])*theoryWaveU;
U[cellI] = newU;
}
}
// ------Wave output region------
if((xx >= waveOutputRegion0)&&(xx <= waveOutputRegion1))
{
scalar yy = mesh.C()[cellI].y();
scalar waterSurface = this -> waterSurface_;
scalar theoryWaveAlpha1 = 0.0;
vector theoryWaveU = vector::zero;
if(yy <= waterSurface)
{
theoryWaveAlpha1 = 1.0;
}
const scalarList & relaxationCoeff = this -> relaxationCoeff_();
scalar oldAlpha1 = alpha1[cellI];
scalar newAlpha1 = relaxationCoeff[cellI]*oldAlpha1 + (1.0-relaxationCoeff[cellI])*theoryWaveAlpha1;
alpha1[cellI] = newAlpha1;
vector oldU = U[cellI];
vector newU = relaxationCoeff[cellI]*oldU + (1.0-relaxationCoeff[cellI])*theoryWaveU;
U[cellI] = newU;
}
}
}
void vofWaveModel::calcWavePara_stokesV_1st_()
{
scalar g = 9.81;
scalar waveLength0 = mag(g)*wavePeriod*wavePeriod/(2.0*M_PI);
// stokes V
scalar lambda21_MajInit = 0;
scalar L_MajInit = waveLength0;
scalar err_Critical = 1e-10;
label i0, i1, i2;
label i_max = 1e5;
for(i0 = 1; i0 <= i_max; i0++)
{
scalar hh = waterDepth;
scalar lambda21_init = lambda21_MajInit;
scalar L_init = L_MajInit;
scalar L0 = waveLength0;
for (i1 = 1; i1 <= i_max; i1++)
{
scalar kk = 2*M_PI/L_init;
scalar cc = cosh(kk*hh);
scalar ss = sinh(kk*hh);
scalar C1 = ( 8.0*pow(cc,4.0)-8.0*cc*cc+9.0 ) / 8.0 / pow(ss,4.0);
scalar C2 = ( 3840.0*pow(cc,12.0)-4096.0*pow(cc,10.0)+2592*pow(cc,8.0)-1008.0*pow(cc,6.0)+
5944.0*pow(cc,4.0)-1830.0*cc*cc+147.0 ) / ( 512.0*pow(ss,10.0)*(6.0*cc*cc-1.0) );
scalar L_ITER = L0*tanh(kk*hh)*( 1.0+pow(lambda21_init,2.0)*C1+pow(lambda21_init,4.0)*C2 );
if (mag(L_ITER - L_init) < 1e-7)
{
L_init = L_ITER;
break;
}
else
{
L_init = L_ITER;
}
}
scalar kk = 2*M_PI/L_init;
scalar cc = cosh(kk*hh);
scalar ss = sinh(kk*hh);
scalar B33 = 3.0*(8.0*pow(cc,6.0)+1)/64.0/pow(ss,6.0);
scalar B35 = ( 88128.0*pow(cc,14.0)-208224.0*pow(cc,12.0)+70848.0*pow(cc,10.0)
+54000.0*pow(cc,8.0)-21816.0*pow(cc,6.0)+6264*pow(cc,4.0)-54.0*cc*cc-81.0 )
/ ( 12288.0*pow(ss,12.0)*(6.0*cc*cc-1.0) );
scalar B55 = ( 192000.0*pow(cc,16.0)-262720.0*pow(cc,14.0)+83680.0*pow(cc,12.0)
+20160.0*pow(cc,10.0)-7280.0*pow(cc,8.0)+7160.0*pow(cc,6.0)-1800.0*pow(cc,4.0)-1050.0*cc*cc+225.0 )
/ ( 12288.0*pow(ss,10.0)*(6.0*cc*cc-1.0)*(8.0*pow(cc,4.0)-11.0*cc*cc+3.0) );
for (i2 = 1; i2 <= i_max; i2++)
{
scalar waveHeight = this -> waveHeight_;
scalar lambda21_ITER = M_PI*waveHeight / L_init / ( 1.0+pow(lambda21_init,2.0)*B33+pow(lambda21_init,4.0)*(B35-B55) );
if (mag(lambda21_ITER - lambda21_init)<1e-4)
{
break;
}
lambda21_init = lambda21_ITER;
}
scalar err_iter = sqrt( pow((lambda21_init-lambda21_MajInit),2.0) + pow((L_init-L_MajInit),2.0) );
if ( err_iter < err_Critical )
{
break;
}
L_MajInit = L_init;
lambda21_MajInit = lambda21_init;
}
this -> waveLength_ = L_MajInit;
this -> lambda21_ = lambda21_MajInit;
this -> calcWavePara_stokesV_2nd_();
}
void vofWaveModel::calcWavePara_stokesV_2nd_()
{
scalar kk = 2*M_PI/L_init;
scalar hh = waterDepth;
scalar cc = cosh(kk*hh);
scalar ss = sinh(kk*hh);
scalar A11 = 1.0/ss;
scalar A13 = -( cc*cc * (5.0*cc*cc - 1.0) ) / ( 8.0 * pow(ss,5.0) );
scalar A15 = -( 1184.0*pow(cc,10.0)-1440.0*pow(cc,8.0)-1992.0*pow(cc,6.0)
+ 2641.0*pow(cc,4.0)-249.0*cc*cc + 18.0 ) / (1536.0*pow(ss,11.0));
scalar A22 = 3.0/(8.0*pow(ss,4.0));
scalar A24 = ( 192.0*pow(cc,8.0)-424.0*pow(cc,6.0)-312.0*pow(cc,4.0)
+ 480.0*cc*cc-17.0 ) / (768.0*pow(ss,10.0));
scalar A33 = ( 13.0-4.0*cc*cc ) / (64.0*pow(ss,7.0));
scalar A35 = ( 512.0*pow(cc,12.0) + 4224.0*pow(cc,10.0)-6800.0*pow(cc,8.0)-12808.0*pow(cc,6.0)
+ 16704.0*pow(cc,4.0)-3154.0*cc*cc + 107.0 ) / ( 4096.0*pow(ss,13.0)*(6.0*pow(cc,2.0)-1.0) );
scalar A44 = ( 80.0*pow(cc,6.0)-816.0*pow(cc,4.0) + 1338.0*cc*cc-197.0 ) / (1536.0*pow(ss,10.0)*(6.0*pow(cc,2.0)-1.0));
scalar A55 = -( 2280.0*pow(cc,10.0)-72480.0*pow(cc,8.0) + 324000.0*pow(cc,6.0)-432000.0*pow(cc,4.0)
+ 163470.0*cc*cc-16245.0 )/ ( 61440.0*pow(ss,11.0)*(6.0*pow(cc,2.0)-1.0)*(8.0*pow(cc,4.0)-11.0*pow(cc,2.0) + 3.0) );
scalar lambda11 = lambda21*A11 + pow(lambda21,3.0)*A13 + pow(lambda21,5.0)*A15;
scalar lambda12 = pow(lambda21,2.0)*A22 + pow(lambda21,4.0)*A24;
scalar lambda13 = pow(lambda21,3.0)*A33 + pow(lambda21,5.0)*A35;
scalar lambda14 = pow(lambda21,4.0)*A44;
scalar lambda15 = pow(lambda21,5.0)*A55;
scalar B22 = cc*(2.0*pow(cc,2.0) - 1.0) / (4.0*pow(ss,3.0));
scalar B24 = cc*( 272.0*pow(cc,8.0)-504.0*pow(cc,6.0)-192.0*pow(cc,4.0) + 322.0*pow(cc,2.0) + 21.0 ) / (384.0*pow(ss,9.0));
scalar B44 = cc*( 768.0*pow(cc,10.0)-488.0*pow(cc,8.0)-48.0*pow(cc,6.0)
+ 48.0*pow(cc,4.0) + 106.0*pow(cc,2.0)-21.0) / ( 384.0*pow(ss,9.0)*(6.0*pow(cc,2.0)-1.0) );
scalar B33 = 3.0*(8.0*pow(cc,6.0)+1)/64.0/pow(ss,6.0);
scalar B35 = ( 88128.0*pow(cc,14.0)-208224.0*pow(cc,12.0)+70848.0*pow(cc,10.0)
+54000.0*pow(cc,8.0)-21816.0*pow(cc,6.0)+6264*pow(cc,4.0)-54.0*cc*cc-81.0 )
/ ( 12288.0*pow(ss,12.0)*(6.0*cc*cc-1.0) );
scalar B55 = ( 192000.0*pow(cc,16.0)-262720.0*pow(cc,14.0)+83680.0*pow(cc,12.0)
+20160.0*pow(cc,10.0)-7280.0*pow(cc,8.0)+7160.0*pow(cc,6.0)-1800.0*pow(cc,4.0)-1050.0*cc*cc+225.0 )
/ ( 12288.0*pow(ss,10.0)*(6.0*cc*cc-1.0)*(8.0*pow(cc,4.0)-11.0*cc*cc+3.0) );
scalar lambda22 = pow(lambda21,2.0)*B22 + pow(lambda21,4.0)*B24;
scalar lambda23 = pow(lambda21,3.0)*B33 + pow(lambda21,5.0)*B35;
scalar lambda24 = pow(lambda21,4.0)*B44;
scalar lambda25 = pow(lambda21,5.0)*B55;
scalar C0 = sqrt(g_mag * tanh(kk * hh));
scalar C1 = (8.0 * pow(cc, 4.0) - 8.0 * cc * cc + 9.0) / (8.0 * pow(ss, 4.0));
scalar C2 = (3840.0 * pow(cc, 12.0) - 4096.0 * pow(cc, 10.0) + 2592.0 * pow(cc, 8.0)
- 1008.0 * pow(cc, 6.0) + 5944.0 * pow(cc, 4.0) - 1830.0 * cc * cc + 147.0)
/ ( 512.0 * pow(ss, 10.0) * (6.0 * cc * cc - 1.0));
scalar cMean = C0 * sqrt((1.0 / kk) * (1.0 + pow(lambda21, 2.0) * C1 + pow(lambda21, 4.0) * C2));
}
scalar vofWaveModel::caliU_() const
{
scalar caliU;
caliU = waveHeight*waveHeight*waveOmega/8.0/tanh(waveNumber*waterDepth)/waterDepth
-waveOmega*waveNumber*waveNumber*pow(waveHeight, 4.0)/64.0/sinh(2.0*waveNumber*waterDepth)
+waveOmega*waveNumber*waveNumber*pow(waveHeight, 4.0)*cosh(waveNumber*waterDepth)
*(cosh(2.0*waveNumber*waterDepth)+2.0)/256.0/pow(sinh(waveNumber*waterDepth),3.0)
+3.0*waveOmega*waveNumber*waveNumber*pow(waveHeight,4.0)*sinh(2.0*waveNumber*waterDepth)/256.0
/pow(sinh(waveNumber*waterDepth),4.0)+3.0*waveOmega*waveNumber*waveNumber*pow(waveHeight,4.0)
*cosh(waveNumber*waterDepth)*cosh(2.0*waveNumber*waterDepth)*(cosh(2.0*waveNumber*waterDepth)+2.0)
/512.0/pow(sinh(waveNumber*waterDepth),7.0);
return caliU;
}
#include "vofCwriteControl.H"
#endif
 MATLAB中的数值方法实现:从一阶到高阶偏微分方程求解
MATLAB中的数值方法实现:从一阶到高阶偏微分方程求解




 文章展示了MATLAB中用于解决不同类型的偏微分方程(PDEs)的代码示例,包括一阶、二阶和三阶方法,如Gauss-Seidel、多网格和有限差分法。这些示例说明了如何在实际问题中应用数值方法来近似求解复杂的PDEs。
文章展示了MATLAB中用于解决不同类型的偏微分方程(PDEs)的代码示例,包括一阶、二阶和三阶方法,如Gauss-Seidel、多网格和有限差分法。这些示例说明了如何在实际问题中应用数值方法来近似求解复杂的PDEs。

















 186
186

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










