t3
main3t.m
clearvars; clc; % main3t.m
guesses = [4; 8; 11];
kls = zeros(size(guesses, 1), 1);
lambdas = zeros(size(kls, 1), 1);
for ii = 1: size(kls, 1)
kl = fzero(@func, guesses(ii, 1));
kls(ii, 1) = kl;
% disp(kl*kl);
lambdas(ii, 1) = get_lambda(kl);
end
fig = figure(1);
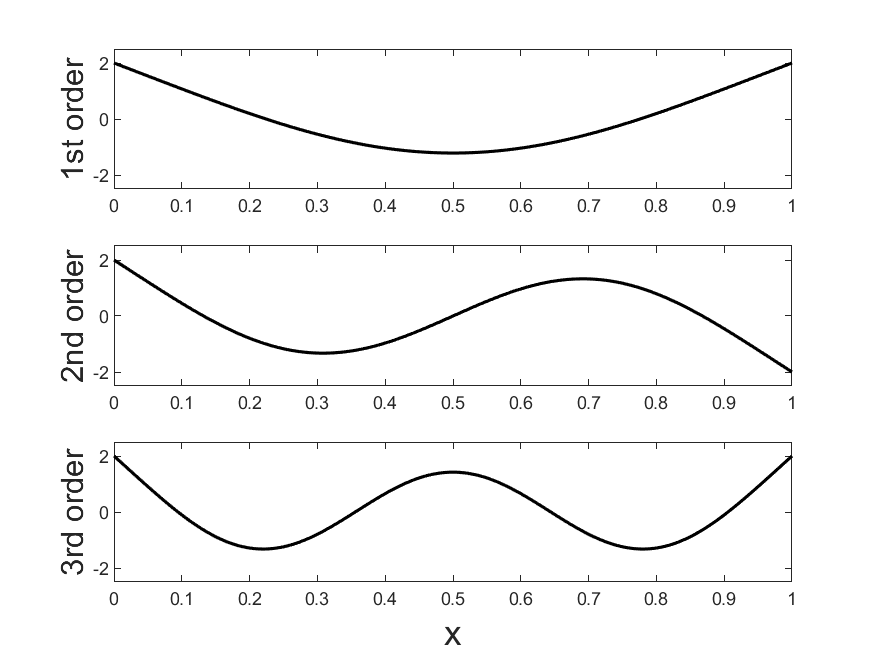
strs = ["1st"; "2nd"; "3rd"];
for jj = 1: 3
subplot(3, 1, jj);
xx = 0: 0.001: 1;
xx = xx';
yy = zeros(size(xx, 1), 1);
for ii = 1: size(yy, 1)
yy(ii, 1) = get_Yn(xx(ii, 1), lambdas(jj, 1), kls(jj, 1));
end
plt = plot(xx, yy);
fig.CurrentAxes.YLim = [-2.5, 2.5];
plt.Color = "Black";
plt.LineWidth = 1.5;
yl = ylabel(strs(jj, 1)+" order");
yl.FontSize = 15;
end
xl = xlabel("x");
xl.FontSize = 17;
saveas(fig, './fig-mode.png');
close(fig);
function F = func(x)
F = cos(x) * cosh(x) - 1;
end
function lambda = get_lambda(kl)
lambda = (cosh(kl) - cos(kl)) / (sinh(kl) - sin(kl));
end
function Yn = get_Yn(xx, lambda_n, k_n)
Yn = cosh(k_n*xx) + cos(k_n*xx) - lambda_n*(sinh(k_n*xx) + sin(k_n*xx));
end
t4
clearvars; clc; % main4t.m
[m1, m2, omega] = ...
deal(1e04, 8e04, 120*pi);
% deal(1e04, 8e04, 40*pi);
% deal(4e03, 2e04, 200*pi);
k1 = 2e08;
k2 = 1e06;
Q_max = 160;
AA = [-m1*omega^2+k1+k2, -k2;
-k2, -m2*omega^2+k2];
bb = [0; Q_max];
xx = AA\bb;
A1 = xx(1, 1);
A2 = xx(2, 1);
F_max = k1*abs(A1);
T_F = F_max/Q_max;
eff = 1 - T_F;
disp("eff = "+num2str(eff*100)+" % ");
t5
clearvars; clc; % main5t.m
% [m1, m2, m3] = deal(23, 23, 26);
[m1, m2, m3] = deal(40, 40, 60);
[k1, k2, k3] = deal(954, 1312, 1640);
syms omega;
AA = [k1-omega^2*m1, -k1, 0;
-k1, k1+k2-omega^2*m2, -k2;
0, -k2, k2+k3-omega^2*m3];
eqn = det(AA) == 0;
omegas = solve(eqn, omega);
omegas = double([omegas]);
omegas = sort(omegas);
omegas = omegas(4:end, 1);
UU = zeros(size(omegas, 1), size(omegas, 1));
for ii = 1: size(omegas, 1)
AA_num = subs(AA, omega, omegas(ii, 1));
AA_num = double(AA_num);
[VV, DD] = eig(AA_num);
eps = 1e-08;
for jj = 1: size(DD, 1)
if abs(DD(jj, jj)) <= eps
UU(:, ii) = VV(:, jj);
end
end
end
MM = [m1, 0, 0; 0, m2, 0; 0, 0, m3];
MM = UU'*MM*UU;
MM = diag(MM);
KK = [k1, -k1, 0; -k1, k1+k2, -k2; 0, -k2, k2+k3];
KK = UU'*KK*UU;
KK = diag(KK);
FF = [1; 0; 0];
FF = UU'*FF;
lowers = zeros(size(FF, 1), 1);
for ii = 1: size(lowers, 1)
lowers(ii, 1) = KK(ii, 1)/FF(ii, 1)^2;
end
Omega = [0.8*omegas(2 ,1); (omegas(1 ,1)+omegas(3 ,1))/2];
Amp = zeros(size(FF, 1), 2);
for ii = 1: size(Amp, 1)
Amp(ii, 1) = 1/(lowers(ii, 1)*(1 - Omega(1, 1)^2/omegas(ii, 1)^2));
Amp(ii, 2) = 1/(lowers(ii, 1)*(1 - Omega(2, 1)^2/omegas(ii, 1)^2));
end
for ii = 1: size(omegas, 1)
% disp(omegas(ii, 1)^2);
end
Amp = Amp';
t6
clearvars; clc; % main6t.m
timeN = 128;
obj = solution(timeN);
obj.solve();
% solution.m
classdef solution
properties (Access = private)
timeN;
end
methods
function obj = solution(timeN)
obj.timeN = timeN;
end
function solve(obj)
[M, K, P] = obj.get_MKP();
objPIM = PIM(obj.timeN);
objPIM.solve(M, K, P);
objWilson = Wilson(obj.timeN);
objWilson.solve(M, K, P);
alpha = 1/2;
beta = 1/6;
objNewmark = Newmark(obj.timeN, alpha, beta);
objNewmark.solve(M, K, P);
alpha = 1/4;
beta = 1/2;
objNewmark = Newmark(obj.timeN, alpha, beta);
objNewmark.solve(M, K, P);
end
end
methods (Access = private)
function [M, K, P] = get_MKP(~)
M = [660, 0; 0, 1360];
% K = [1747968.75, -1747968.75;
% -1747968.75, 1843638.75];
P = [60000; 0];
% P = [10000; 0];
E = 120*10^9;
% E = 200*10^9;
l1 = 160*10^(-2);
I1 = 497.2*10^(-8);
l2 = 200*10^(-2);
I2 = 212.6*10^(-8);
k1 = get_k1(E, I1, l1);
k2 = get_k2(E, I2, l2);
K = [k1, -k1; -k1, k1 + k2];
% disp(K);
function k1 = get_k1(E, I, l)
k1 = (12.0*E*I)/l^3;
end
function k2 = get_k2(E, I, l)
k2 = (3.0*E*I)/l^3;
end
disp(k2);
end
end
end
% PIM.m
classdef PIM
properties (Access = private)
timeN;
end
methods
function obj = PIM(timeN)
obj.timeN = timeN;
end
function solve(obj, M, K, P)
N = obj.timeN;
G = zeros(2, 2);
A = -inv(M)*G/2;
B = G/M*G/4-K;
C = -G/M/2;
D = inv(M);
f = [0; 0; P];
H = [A, D; B, C];
tau = 1/N;
m = 2^N;
t = tau/m;
I = eye(size(H));
Ta = H*t + (H*t)^2*(I+(H*t)/3+(H*t)^2/12)/2;
for ii = 1 : N
Ta = 2*Ta+Ta^2;
end
T = I+Ta;
v = zeros(4,(N+2));
for j = 1 : (N+2)
v(:, j+1) = T*(v(:,j) + H\f)- H\f;
end
u3 = v(1: 2, 2: (N+2));
t0 = 0: tau: 1;
fig = figure(1);
plts = [];
strs = [];
plt = plot(t0, u3(1, :));
hold on;
plt.Color = "Red";
plt.LineWidth = 1.5;
plt.LineStyle = "--";
str = "x_{1}";
plts = [plts; plt];
strs = [strs; str];
plt = plot(t0, u3(2, :));
hold on;
plt.Color = "Black";
plt.LineStyle = "-";
plt.LineWidth = 1.5;
str = "x_{2}";
plts = [plts; plt];
strs = [strs; str];
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
ld.Location = "Best";
xl = xlabel('time(s)');
xl.FontSize = 17;
yl = ylabel('displacement(m)');
yl.FontSize = 17;
tl = title('精细积分法');
tl.FontSize = 17;
fig.CurrentAxes.YLim = [-0.3, 1.8];
saveas(fig, './fig-PIM.png');
close(fig);
end
end
end
% Wilson.m
classdef Wilson
properties (Access = private)
timeN;
end
methods
function obj = Wilson(timeN)
obj.timeN = timeN;
end
function solve(obj, M, K, P)
N = obj.timeN;
u(:, 1) = [0; 0];
v(:, 1) = [0; 0];
w(:, 1) = [P(1, 1)/ M(1, 1); P(2,1)];
theta = 1.55;
h = 1/N;
a = [6/(theta*h)^2, 3/(theta*h), 6/(theta*h), ...
(theta*h)/2, 6/(theta*(theta*h)^2), ...
6/(theta*(theta*h)), 1-3/theta, h/2, h^2/6];
Kn = K+a(1)*M;
Pn = zeros(2, N+3);
Un = zeros(2, N+3);
for ii = 1: (N+2)
Pn(:, ii+1) = P+M*(a(1)*u(:, ii)+a(3)*v(:, ii)+2*w(:, ii));
Un(:, ii+1) = Kn\Pn(:, ii+1);
w(:, ii+1) = a(5)*(Un(:, ii+1)-u(:, ii))-a(6)*v(:, ii)+a(7)*w(:, ii);
v(:, ii+1) = v(:, ii)+a(8)*(w(:, ii+1)+w(:, ii));
u(:,ii+1) = u(:, ii)+h* v(:, ii)+a(9)*(w(:, ii+1)+2*w(:, ii));
end
u2 = u(:, 2: (N+2));
t0 = 0: h: 1;
fig = figure(1);
plts = [];
strs = [];
plt = plot(t0, u2(1, :));
hold on;
plt.Color = "Red";
plt.LineWidth = 1.5;
plt.LineStyle = "--";
str = "x_{1}";
plts = [plts; plt];
strs = [strs; str];
plt = plot(t0, u2(2, :));
hold on;
plt.Color = "Black";
plt.LineStyle = "-";
plt.LineWidth = 1.5;
str = "x_{2}";
plts = [plts; plt];
strs = [strs; str];
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
ld.Location = "Best";
xl = xlabel('time(s)');
xl.FontSize = 17;
yl = ylabel('displacement(m)');
yl.FontSize = 17;
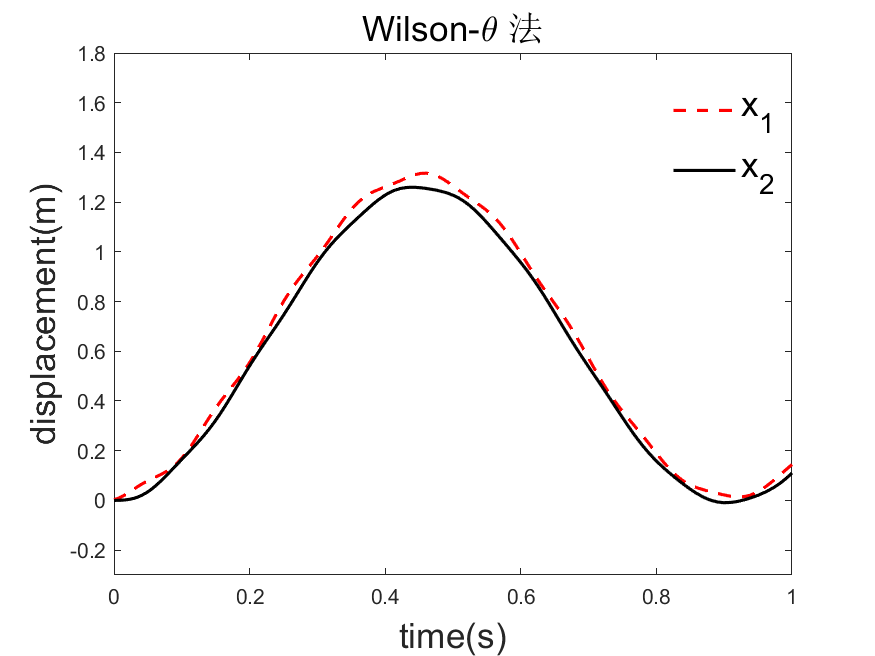
tl = title('Wilson-\theta 法');
tl.FontSize = 17;
fig.CurrentAxes.YLim = [-0.3, 1.8];
saveas(fig, './fig-Wilson.png');
close(fig);
end
end
end
% Newmark.m
classdef Newmark
properties (Access = private)
timeN;
alpha_;
beta_;
end
methods
function obj = Newmark(timeN, alpha, beta)
obj.timeN = timeN;
obj.alpha_ = alpha;
obj.beta_ = beta;
end
function solve(obj, M, K, P)
N = obj.timeN;
alpha = obj.alpha_;
beta = obj.beta_;
h = 1/N;
u(:, 1) = [0; 0];
v(:, 1) = [0; 0];
w(:, 1) = [P(1, 1)/ M(1, 1); P(2,1)];
a = [1/( alpha*h^2), beta/(alpha*h), ...
1/(alpha*h), 1/(2*alpha)-1, ...
beta/ alpha-1, 0.5*h*(beta/alpha-2), ...
h*(1-beta), beta*h];
Kn = K+a(1)*M;
Pn = zeros(2, N+3);
for ii = 1: (N+2)
Pn(:, ii+1) = P+M*(a(1)*u(:, ii)+a(3)*v(:, ii)+a(4)*w(:, ii));
u(:, ii+1) = Kn\Pn(:, ii+1);
w(:, ii+1) = a(1)*(u(:, ii+1)-u(:, ii))-a(3)*v(:, ii)-a(4)*w(:, ii);
v(:, ii+1) = v(:, ii)+a(7)*w(:, ii)+a(8)*w(:, ii+1);
end
u1 = u(:, 2: (N+2));
t0 = 0: h: 1;
fig = figure(1);
plts = [];
strs = [];
plt = plot(t0, u1(1, :));
hold on;
plt.Color = "Red";
plt.LineWidth = 1.5;
plt.LineStyle = "--";
str = "x_{1}";
plts = [plts; plt];
strs = [strs; str];
plt = plot(t0,u1(2,:));
hold on;
plt.Color = "Black";
plt.LineStyle = "-";
plt.LineWidth = 1.5;
str = "x_{2}";
plts = [plts; plt];
strs = [strs; str];
ld = legend(plts, strs);
ld.FontSize = 17;
ld.Box = 'off';
ld.Location = "Best";
xl = xlabel('time(s)');
xl.FontSize = 17;
yl = ylabel('displacement(m)');
yl.FontSize = 17;
tl = title('Newmark-\beta 法');
tl.FontSize = 17;
fig.CurrentAxes.YLim = [-0.3, 1.8];
file_name = './fig-Newmark';
beta = 1/beta;
alpha = 1/alpha;
file_name = [file_name, num2str(alpha)];
file_name = [file_name, num2str(beta)];
file_name = [file_name, '.png'];
saveas(fig, file_name);
close(fig);
end
end
end
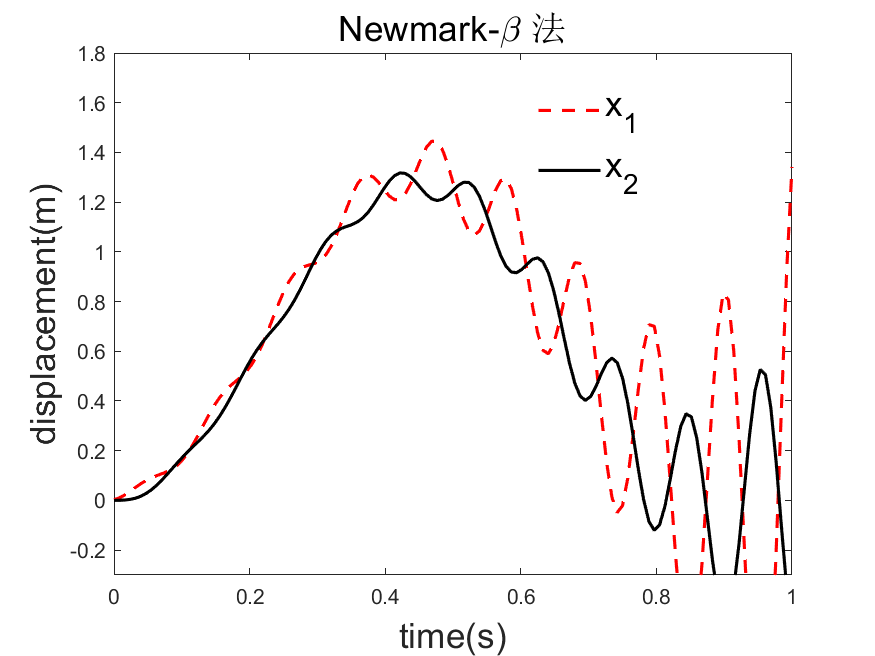
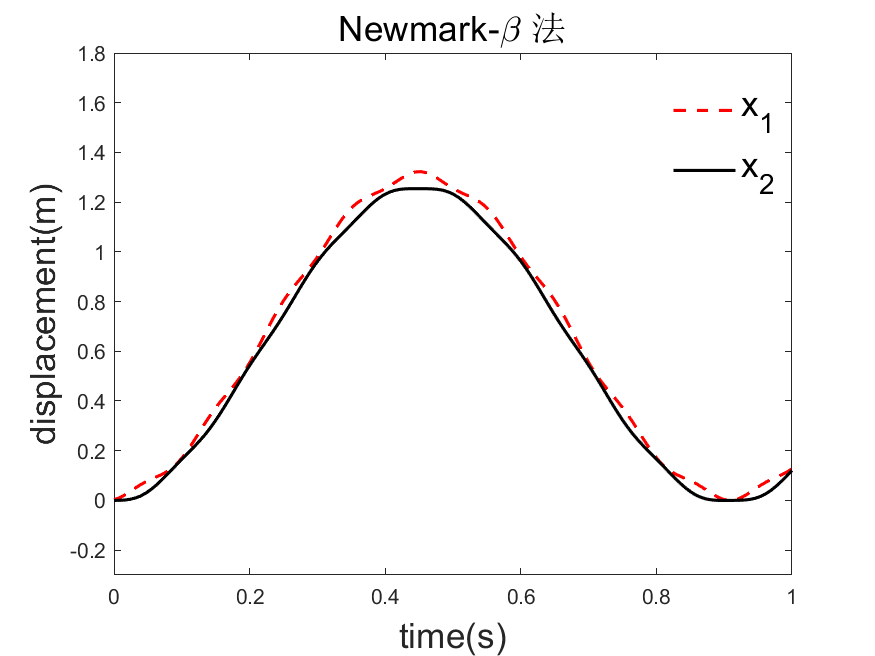
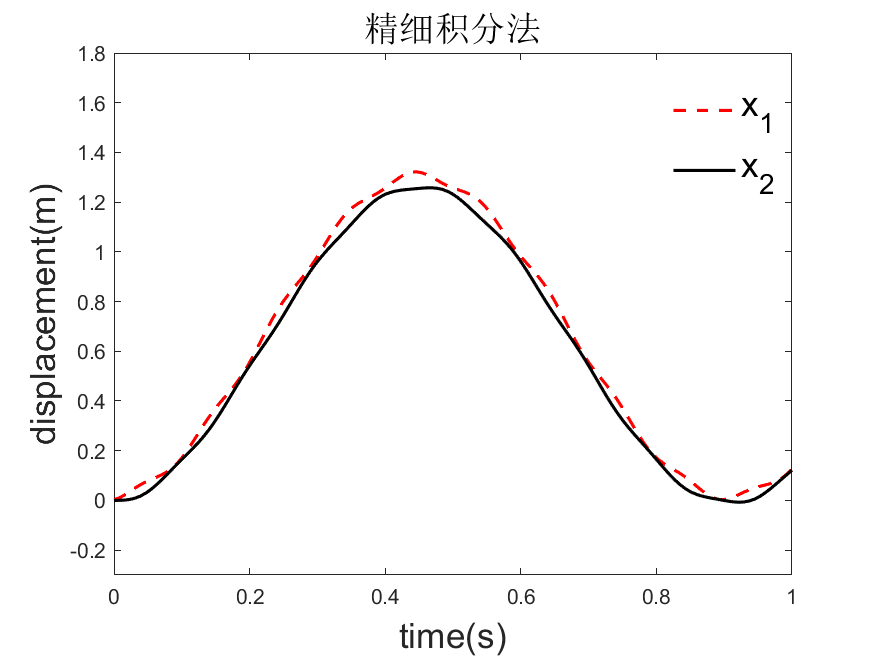




 代码示例展示了使用MATLAB进行数值计算,包括牛顿迭代法求解函数零点、振动系统频率分析以及三种不同的时域数值积分方法(精细积分法、Wilson-θ法、Newmark-β法)来解决结构动力学问题,涉及刚度矩阵、质量矩阵和外部载荷的处理。
代码示例展示了使用MATLAB进行数值计算,包括牛顿迭代法求解函数零点、振动系统频率分析以及三种不同的时域数值积分方法(精细积分法、Wilson-θ法、Newmark-β法)来解决结构动力学问题,涉及刚度矩阵、质量矩阵和外部载荷的处理。

















 197
197

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










