COT论文笔记(4)
论文名称:Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters
本博客范围:P9-P11
出现在这个框里的是我的补充,不是原文。
之前的部分可以查看我的主页QAQ
博主是研究生,为爱发电,大家点赞我会很开心的!谢谢喵。
本系列其他内容
目录
5.3. 分析结果:带验证器的搜索在推理时的扩展情况
我们现在展示对比各种搜索算法的结果,并确定一种与提示难度相关的、针对搜索方法的计算最优扩展策略。
对比搜索算法:我们首先对各种搜索设置进行全面考察。除了标准的“N个答案中最优”方法外,我们还考察了区分不同树搜索方法的两个主要参数:束宽度(M)和前瞻步数(k)。尽管我们无法对每一种配置都进行详尽考察,但我们在最大预算为256的情况下对以下设置进行了考察:
- 束搜索,其束宽度设置 N \sqrt{N} N,其中 N N N为生成预算。
- 束搜索,其固定束宽度为4。
- 对上述束搜索设置1)和2)均应用 k = 3 k = 3 k=3的前瞻搜索。
- 对束搜索设置1)应用 k = 1 k = 1 k=1的前瞻搜索。
为了公平地将搜索方法作为生成预算的函数进行比较,我们制定了一个用于估算每种方法成本的协议。我们将一次生成视为从基础大型语言模型中采样得到的一个答案。
单位1:一个完整的答案
beam搜索:beam数
best of N:N
前瞻: N × ( k + 1 ) N×(k + 1) N×(k+1)
对于束搜索和“N个最佳”方法而言,生成预算分别对应束的数量和 N N N。然而,前瞻搜索会利用额外的计算资源:在推理的每一步中,我们会额外向前采样 k k k步。因此,我们将前瞻搜索的成本定义为 N × ( k + 1 ) N×(k + 1) N×(k+1)次采样。
结果。如图3(左)所示
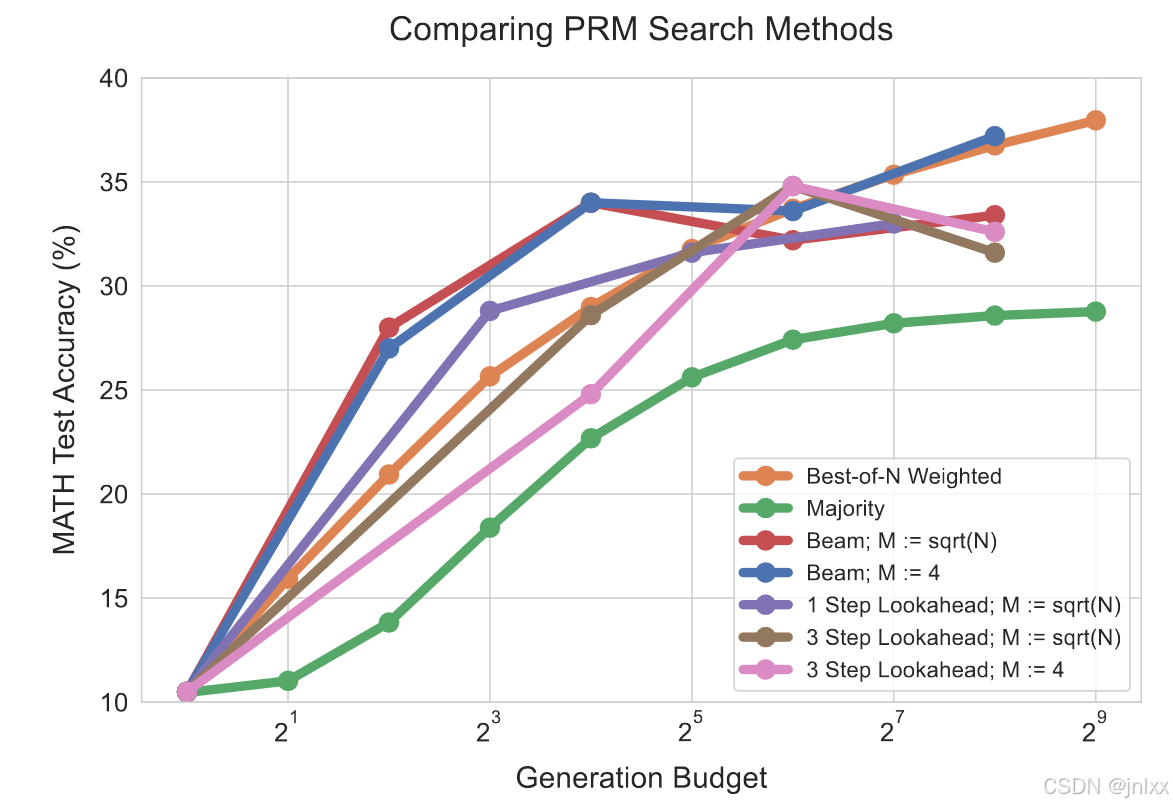
在生成预算较小时,束搜索(红蓝)的表现明显优于“N个答案中最优”(橙)方法。然而,随着预算增加,这些优势大幅减弱,束搜索的表现常常逊于“N个答案中最优”这一基准方法。

我们还发现,在相同的生成预算下,前瞻搜索通常比其他方法表现更差,这很可能是由于模拟前瞻推演而引入了额外的计算量。搜索带来的收益递减很可能是因为对PRM预测结果的过度利用。例如,我们发现有些情况(比如在图29中所示的情况),搜索会导致模型在解决方案的末尾生成信息量低且重复的步骤。
图29:古怪单位翻译
如果4 daps等于7 yaps,5 yaps等于3 baps,那么多少daps等于42 baps?
| 步骤 | 分数 |
|---|---|
| 所以4个daps等于7个yaps,这意味着1个dap等于7/4个yaps或者1.75个yaps | 0.21 |
| 而5个yaps等于3个baps,这意味着1个yap等于3/5个baps或者0.6个baps | 0.32 |
| 我们可以将这些值代入以找到答案 | 0.31 |
| 所以42个baps等于42/0.6个yaps或者70个yaps | 0.60 |
| 而70个yaps等于70/1.75个daps或者40个daps | 0.87 |
| 所以答案是 40 \boxed{40} 40 | 0.92 |
| 我们完成了! | 0.91 |
| 这是我们的最终答案 | 0.90 |
| 空 | 0.91 |
| 所以40个daps等于42个baps | 0.90 |
| 我们完成了! | 0.91 |
| 这就是最后的结果 | 0.90 |
| 空 | 0.64 |
| 空 | 0.78 |
| #### 40 | 0.83 |
后几步概率都很高,但是一直都是废话。
在其他情况下,我们发现过度优化搜索可能会导致生成的解决方案过短,仅包含1到2个步骤。这就解释了为什么功能最强大的搜索方法(即前瞻搜索)表现最差。我们在附录M中包含了通过搜索发现的几个此类示例。
| 内容 | 分数 |
|---|---|
| 无穷等比数列 { 1 4 , 1 8 , 1 16 , ⋯ } \left\{\frac{1}{4},\frac{1}{8},\frac{1}{16},\cdots\right\} {41,81,161,⋯}的前 n n n项和为 255 512 \frac{255}{512} 512255,求 n n n。 | - |
| 该数列前 n n n项和就是 a ( 1 − r n ) 1 − r \frac{a(1 - r^{n})}{1 - r} 1−ra(1−rn),其中 a a a是数列的首项, r r r是公比。 | 0.085 |
| 如果我们对这个特定数列求前 n n n项和并令其等于 255 512 \frac{255}{512} 512255,我们得到 n = 7 n = \boxed{7} n=7。 | 0.11 |
| 实际上, 255 512 \frac{255}{512} 512255的十进制展开中并没有7。 | 0.10 |
| 对,所以我们可以设 1 4 ( 1 − ( 1 2 ) n ) 1 − 1 2 = 255 512 \frac{\frac{1}{4}(1-\left(\frac{1}{2}\right)^{n})}{1-\frac{1}{2}}=\frac{255}{512} 1−2141(1−(21)n)=512255,然后求解 n n n。 | 0.10 |
| 所以我们得到 n = 7 n = 7 n=7。 | 0.10 |
| 这得出 1 − ( 1 2 ) n = 255 256 1-\left(\frac{1}{2}\right)^{n}=\frac{255}{256} 1−(21)n=256255。 | 0.15 |
| 所以, 1 − ( 1 2 ) n = 255 256 1-\left(\frac{1}{2}\right)^{n}=\frac{255}{256} 1−(21)n=256255,然后求解 n n n。 | 0.15 |
| 7 7 7 | 0.30 |
第二步就出结果了,非常显然思考不充分。
搜索能改善哪些问题呢?为了了解如何以计算最优的方式扩展搜索方法,我们现在进行难度区间分析。
整体上比不了best of N,说不定在某些局部表现良好呢。
具体而言,我们将束搜索(束宽度(M = 4))与“N个答案中最优”方法进行对比。在图3(右)中我们可以看到,
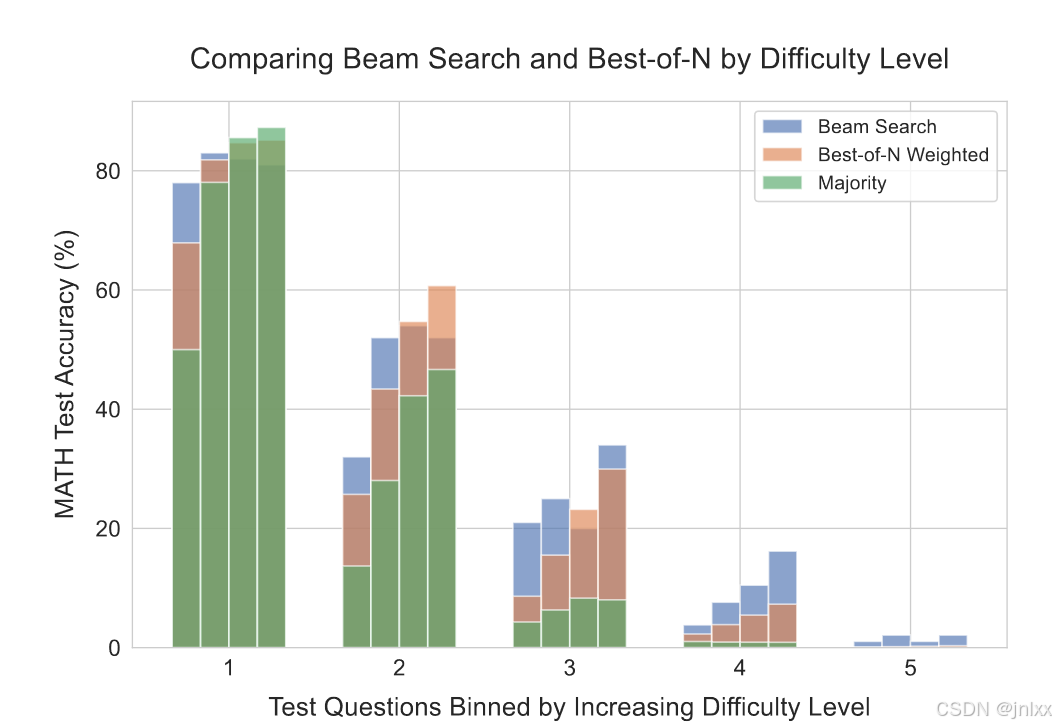
这个图不止三个颜色,是因为把三个柱子叠放且不透明度50%
难题beam效果更好,但是太难了大家都寄了。
虽然总体而言,在生成预算较高时,束搜索和“N个答案中最优”方法的表现相近,但通过对不同难度区间评估它们的效果,却呈现出截然不同的趋势。对于简单问题(难度等级1和2),作为两种方法中更强的优化器,束搜索在生成预算增加时,其性能反而下降,这表明存在对概率关系模型信号过度利用的迹象。相反,对于较难的问题(难度等级3和4),束搜索始终优于“N个答案中最优”方法。而对于最难的问题(难度等级5),没有哪种方法能取得多大有意义的进展。
这些发现与直觉相符:我们可能会预期,对于简单的问题,验证器对正确性的评估大多会是正确的。因此,通过(beam search)进行进一步优化时,我们只会进一步放大验证器所学到的任何虚假特征,从而导致性能下降。
简而言之,容易过拟合,过拟合的部分就是所谓“虚假特征”
而对于更难的问题,基础模型一开始就不太可能采到正确答案,所以搜索能够有助于引导模型更频繁地生成正确答案。
问题难的时候,高强度的拟合就不“过”了。
**计算最优搜索。**鉴于上述结果,显然问题难度可以作为一项有用的统计数据,用于预测在给定计算预算下应采用的最优搜索策略。此外,搜索策略的最佳选择会随着这一难度统计数据的变化而发生极大的变动。因此,我们将“计算最优”的扩展趋势进行了可视化呈现,如图4中,每个难度级别下表现最佳的搜索策略所示。
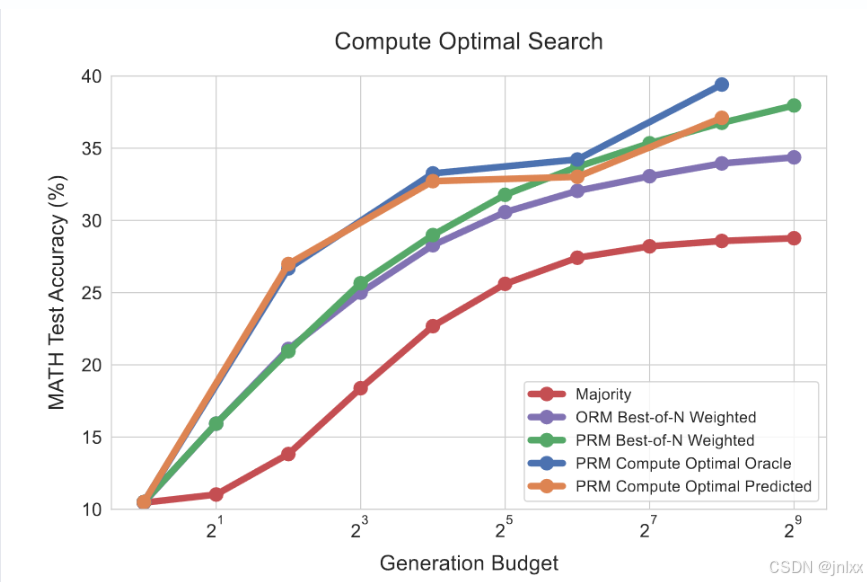
在论文笔记(2)的最后,我们训练了一个“难度预测者”,现在是排上用场的时候了。
如果是难题,beam search。如果是简单题best of N。
竖着看,蓝线(基于真实难度)和橙线(基于预测难度)在同计算能力前提下,解题能力上吊打了绿紫(没有根据难度选择)
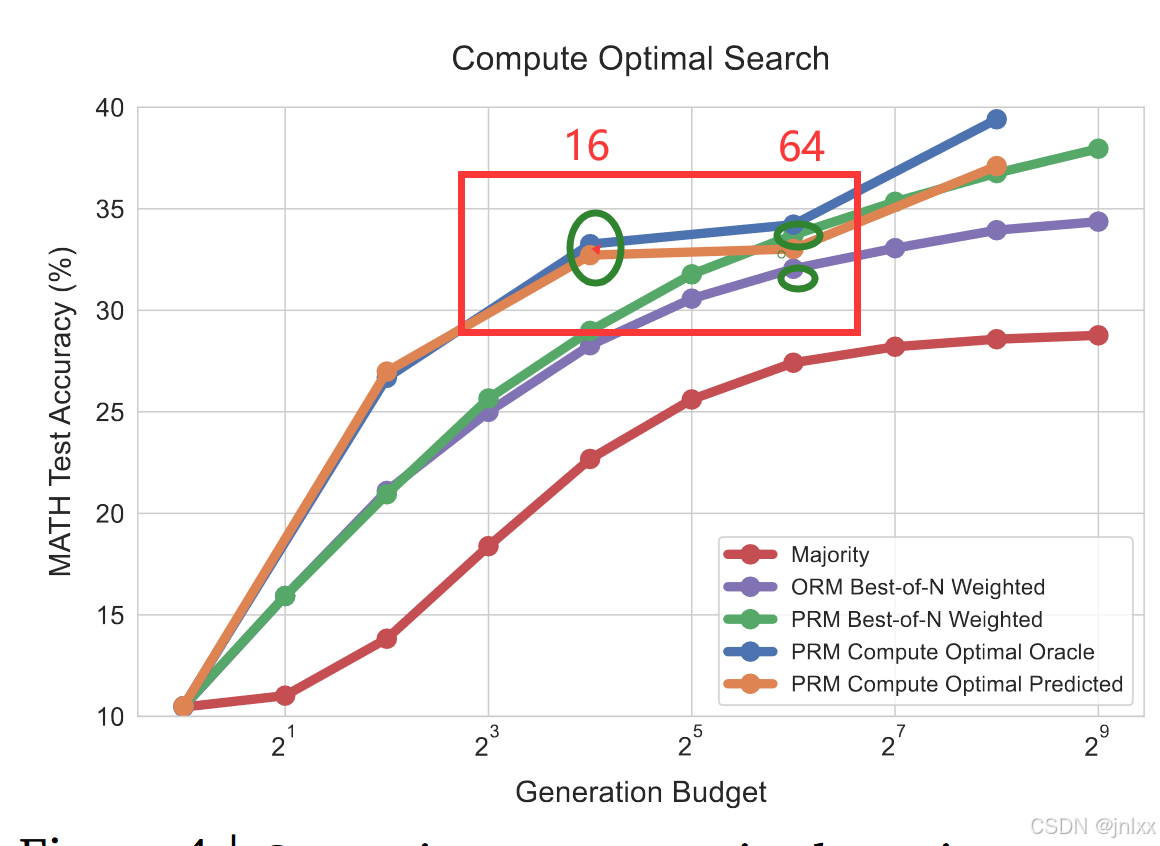
横着看,橙线(基于预测难度)只需要绿紫1/4的计算资源就能达到一样的效果。
而在预算较高的情况下,随着使用预测难度,这些优势中的一部分会有所减弱,但使用神谕区间时,我们仍能看到通过对测试时间计算进行最优扩展而持续获得的改进。这一结果展示了在搜索过程中自适应分配测试时间计算所能带来的性能提升。
我们训练的“难度预测者’还是不能全对,它的预测更精准的话,解题效率还能升高。
小结
我们发现,任何给定验证器搜索方法的有效性在很大程度上取决于计算预算以及手头的问题。具体而言,束搜索(beam-search)在较难的问题以及较低计算预算的情况下更为有效,而N次最佳(best-of-N)策略在较简单的问题以及较高预算的情况下更为有效。此外,通过针对给定的问题难度和测试时间计算预算选择最佳搜索设置,我们能够以少达4倍的测试时间计算量近乎胜过N次最佳策略。
束搜索比best of N更省资源,这在算法上是合理的。
beam search是M倍总答案,best of N是N倍,一般M<N(比如M= N \sqrt{N} N)
6. 优化提议分布
到目前为止,我们研究了针对验证器的搜索在测试时间计算扩展方面的特性。现在,我们将转而研究修改提议分布(第2节)的扩展特性。具体而言,我们让模型能够迭代地修正自身的答案,使模型能够在测试时动态地改进自身的分布。仅仅提示现有的大型语言模型(LLMs)去纠正自身的错误,对于在推理问题上获得性能提升往往收效甚微[15]。因此,我们以曲等人[28]所提出的方法为基础,结合我们设定的情况进行修改,并对语言模型进行微调,使其能够迭代地修正自身的答案。
我们首先描述如何训练和使用那些通过依据自身此前对问题的尝试结果依次进行条件设定,从而优化自身提议分布的模型。然后,我们会分析修正模型在推理时间的扩展特性。
6.1. 准备工作:修正模型的训练与使用
我们微调修正模型的流程与[28]中所述的类似,不过我们引入了一些关键的差异。
对于微调而言,我们需要由一系列错误答案及随后的正确答案构成的轨迹,然后才能基于这些轨迹运行监督微调(SFT)。理想情况下,我们希望正确答案与上下文中提供的错误答案相互关联,以便有效地教会模型隐式地识别上下文中示例里的错误,进而通过进行编辑来纠正这些错误,而不是完全忽略上下文示例,从头再来。
生成修正数据
曲等人[28]提出的获取多轮回滚结果的同策略方法被证明是有效的,但由于运行多轮回滚生成涉及计算成本,在我们的基础设施中该方法并非完全可行。因此,我们在较高的随机性下并行采样64个回复,并事后从这些独立样本中构建多轮生成结果。
具体来说,按照[1]中的方法,我们将每个正确答案与来自该集合的一系列错误答案配对作为上下文,以此构建多轮微调数据。我们在上下文中最多包含四个错误答案,其中上下文中答案的具体数量是从0到4的均匀分布中随机采样得到的。
微调数据形如:
对
错对
错错对
错错错对
错错错错对
我们使用字符编辑距离度量来优先选择与最终正确答案相关的错误答案(见附录H)。需要注意的是,词元编辑距离并非衡量相关性的完美指标,但我们发现这种启发式方法足以将上下文中的错误答案与正确的目标答案相关联,从而有助于训练出有意义的修正模型,而不是将不相关的错误答案和正确答案随意配对。
附录H
为了对修正模型进行微调,我们遵循6.1节中概述的流程。
首先,我们针对每个问题采样64个输出。然后,我们过滤掉所有以无效解结尾的答案。对于每个正确答案,我们随后从0到4之间均匀采样一个数字,该数字表示在训练的上下文中要包含多少个错误答案。正确答案会被用作轨迹(我们训练模型去生成的内容)中的最后一个答案,而错误答案则被包含在上下文中。如果采样得到的数字大于0,**我们会根据字符级编辑距离度量来找到最接近的错误答案,并将其作为轨迹中的最后一个错误答案包含进来。**这样做的目的是选择一个与正确答案有一定相关性的错误答案,以促进学习。
顺序和字符距离相关
对于其余的错误答案,我们从可用答案集合中随机采样。如果采样得到的错误答案数量少于4个,我们会截断均匀分布的最大值,使其与错误样本的数量相匹配。
我们发现,通常而言,在由上述方式生成的轨迹所构成的评估集上评估损失,并不能为提前停止训练提供一个良好的信号。相反,我们发现在评估损失开始上升很久之后的检查点,其修正能力要强得多。这很可能是因为在对修正模型进行微调后,评估集代表的是异策略数据,与模型自身按同策略生成的轨迹相比,自然会出现分布外的情况。因此,我们选择的修正模型检查点是在观察到验证集出现过拟合现象之后的稍晚一点的位置。
我们发现,微调时适当过拟合可以获得更好的修正能力,因为该微调数据集是人为合成的,本身就比较奇怪。
在推理时使用修正
给定一个经过微调的修正模型,我们便可以在测试时从该模型中采样一系列修正结果。虽然我们的修正模型在训练时上下文中最多只包含之前的四个答案,但我们可以通过将上下文截断为最近的四个修正后的回复来采样更长的链。在图6(左)中,我们可以看到,当我们从修正模型中采样更长的链时,模型在每一步的一次通过率(pass@1)会逐渐提高,这表明我们能够有效地教会模型从上下文中之前答案所犯的错误中学习。
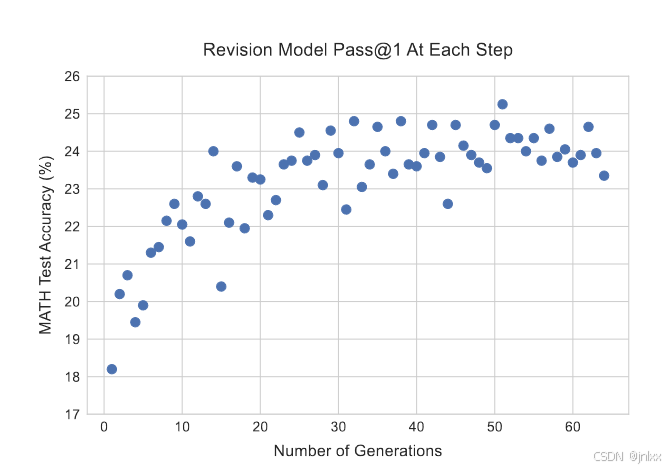
多验算是个好事




















 965
965










