COT论文笔记（2）

原创已于 2025-01-02 17:29:01 修改 · 1.2k 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#论文阅读

于 2024-12-31 03:17:20 首次发布

COT论文笔记（2）

论文名称：Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters
本博客范围：P3-P5

出现在这个框里的是我的补充，不是原文。

2. 测试时计算的统一视角：提议者和验证者

我们首先统一理解利用测试阶段计算的各种方法，然后分析了一些具有代表性的方法。

首先，我们从(在测试阶段依据给定提示自适应地修改模型预测分布)的角度来看待额外测试阶段计算量的使用。

根据题目类型，判断我应该在哪部分多思考一会

理想情况下，测试阶段计算应当对分布进行修改，以便生成比单纯从大型语言模型（LLM）本身采样更好的输出结果。

一般来说，有两个 “调节旋钮” 可促使对大型语言模型分布进行修改：
(1) 在输入层面：通过向给定提示添加一组额外的词元，让大型语言模型依据这些词元来获得修改后的分布；
(2) 在输出层面：从标准语言模型中采样多个候选结果，并对这些候选结果进行处理。

换句话说，我们既可以修改由大型语言模型本身产生的提议分布，使其相较于单纯依据提示的情况有所改进，也可以使用一些事后验证器或评分器来执行输出修改。

让他输出答案前给他一些额外要求
或者
根据输出的答案做二次加工

这个过程让人联想到从复杂目标分布中进行马尔可夫链蒙特卡洛（MCMC）[2] 采样，不过这里是通过结合一个简单的提议分布和一个评分函数来实现的。直接通过改变输入词元来修改提议分布以及使用验证器构成了我们研究的两个独立方向。

分别是本节标题中的提议者和验证者

修改提议分布：
改进提议分布的一种方法是通过受强化学习启发的微调方法（如 STaR 或 ReSTEM [35, 50]）针对给定的推理任务直接对模型进行优化。需要注意的是，这些技术并不使用任何额外的输入词元，而是专门对模型进行微调以产生改进后的提议分布。

这里应该就是传统的微调，修改了参数的

与之不同的是，像自我批判（self - critique）[4, 8, 23, 30] 这类技术能够让模型自身在测试阶段改进其提议分布，方法是指示模型以迭代的方式对自己的输出进行批判和修改。

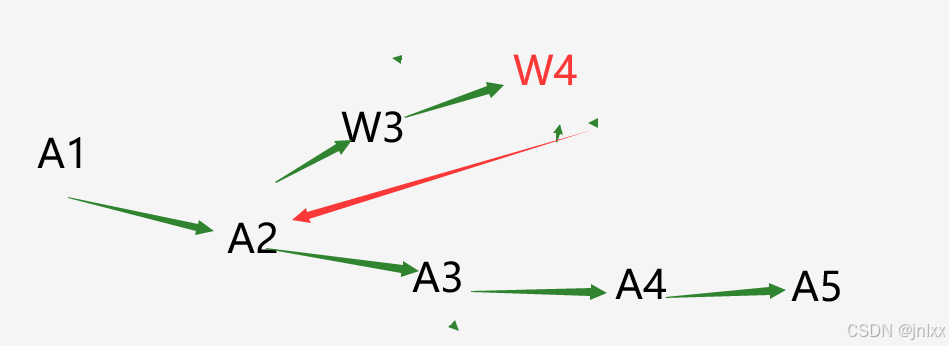
类似搜索探路的思维链，答案形如 $A_1A_2W_3W_4A_2A_3A_4A_5$

一个非常典型的例子
$……A2\boxed{……A_2}$
省略一部分
$W3W4\boxed{W_3W_4}$

可以观察到kimi在这一步矩阵乘法做错了
随后kimi的结果逐步变得变态

他似乎意识到了什么，通过一个生硬的转折“实际上“，倒回了最开始那张图，重新开始
$A2\boxed{A_2}$
并计算成功
$A3A4A5……\boxed{A_3A_4A_5……}$

由于使用现成模型进行提示在测试阶段无法有效地实现有效修改，我们专门针对基于复杂推理的场景对模型进行微调，使其能迭代地修改答案。

“off-the-shelf models” 表示现成的、通用的模型，也就是那些已经被开发出来，未经特定定制或进一步针对性调整，可直接拿来使用的模型。

为此，我们采用了（依据 “最佳 N 选 1” 引导的模型响应改进）来对（on policy数据）进行微调的方法 [28]。

优化验证器。在我们对提议分布和验证器的抽象概念中，验证器用于从提议分布中聚合或选出最佳答案。使用此类验证器最典型的方式是采用“N选最佳”采样，即我们对N个完整的解决方案进行采样，然后依据验证器选出最佳方案[7]。不过，通过训练一个基于过程的验证器[22]，或者说过程奖励模型（PRM），这种方法可以得到进一步改进。
该模型会对解决方案中每个中间步骤的正确性进行预测，而不只是针对最终答案进行预测。然后，我们可以利用这些逐步骤的预测结果，在解决方案空间中进行树搜索，与简单的“N选最佳”方法相比，这使得依据验证器进行搜索有可能变得更高效、更有效[6, 10, 48]。

更多的过程分数，给潜在的搜索或者dp空间。

3. 如何最佳地扩展测试时计算

鉴于各种方法的统一，我们现在想要了解如何最有效地利用测试时的计算来提高语言模型（LM）在给定提示下的性能。具体而言，我们希望解答以下问题：

我们得到了一个提示以及一个用于解决问题的测试时计算预算。在上述抽象概念下，存在不同的利用测试时计算的方法。
根据给定的具体问题，这些方法中的每一种可能或多或少都有成效。我们如何确定针对给定提示利用测试时计算的最有效方式呢？
与仅仅使用一个规模大得多的预训练模型相比，这样做的效果又会如何呢？

在优化提议分布或依据验证器进行搜索时，有几个不同的超参数可以调整，以确定应如何分配测试时的计算预算。
例如，当使用为自我纠错而微调过的模型作为提议分布，并将目标奖励模型（ORM）作为验证器时：

我们既可以将全部测试时计算预算用于从该模型并行生成N个独立样本，然后采用“N选最佳”的方法；
也可以使用修订模型按顺序对N个修订样本进行采样，然后通过目标奖励模型从该序列中选出最佳答案；
或者在这两种极端做法之间寻求一种平衡。

直观来看，我们可能会预期“较简单”的问题能从修订中获益更多，因为模型最初的样本更有可能方向正确，只是可能需要进一步完善。另一方面，具有挑战性的问题可能需要对不同的高层次解题策略进行更多探索，所以在这种情况下，并行多次独立采样或许更可取。

要么逐步完善，要么各做各的。
简单题更适合逐步完善，难题更适合各做各的

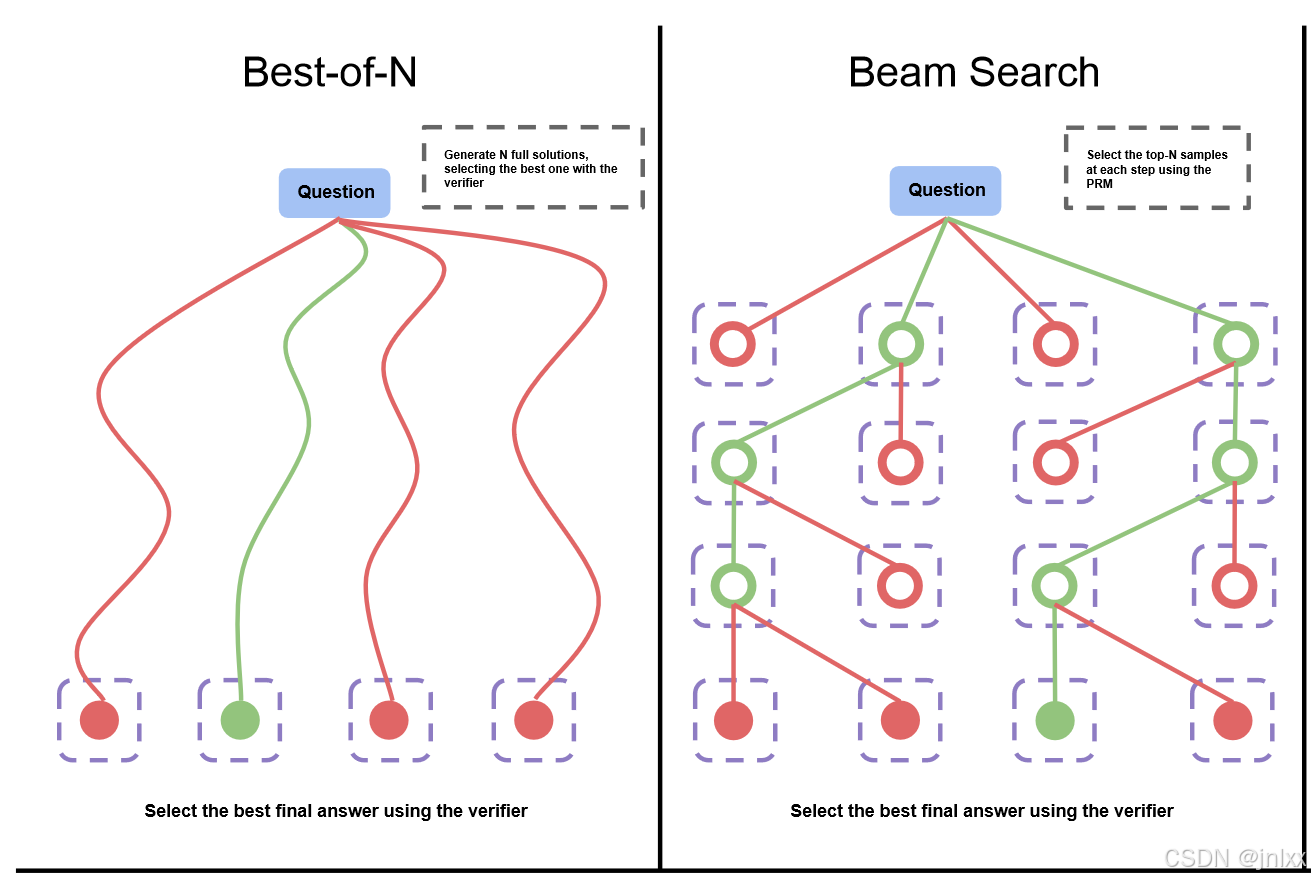
在这里插入图片描述
就验证器而言，我们还可以在不同的搜索算法（例如束搜索、前瞻搜索、“N 选最佳”）之间进行选择，每种算法可能会因手头的验证器和提议分布的质量不同而展现出不同的特性。与更为简单的 “N 选最佳” 或多数投票基准方法相比，在处理更难的问题时，更复杂的搜索程序可能会更有用。

3.1. 测试时计算最优缩放策略

一般而言，我们希望针对给定问题，选择测试时计算预算的最优分配方式。为此，对于任何利用测试时计算的给定方法（例如，本文中的修订以及依据验证器进行搜索，其他地方的各种其他方法），我们将 “测试时计算最优缩放策略” 定义为这样一种策略：它选择与给定测试时策略相对应的超参数，以便在测试时针对给定提示实现最大的性能收益。

输入要解决的问题，输出一个策略

形式上，将 Target (θ, N, q) 定义为模型针对给定提示 q，使用测试时计算超参数 θ 以及计算预算 N 所诱导出的自然语言输出标记的分布。

在N的时间限制下，解决q问题，使用theta策略
输出的是一个分布。

可以理解为，返回的是一个考生小明，卷子是q，考试时间是N，做题策略（比如充分演算放弃难题/放弃演算死磕难题）是theta

我们希望选择能使给定问题的目标分布准确性最大化的超参数 θ。我们将其正式表述如下：
$\theta_{q, a^{*}(q)}^{*}(N) = \operatorname{argmax}_{\theta} \left( \mathbb{E}_{y \sim \text{Target}(\theta, N, q)} \left[ \mathbb{I}_{y = y^{*}(q)} \right] \right),$
其中， $y^*(q)$ 表示针对提示 $q$ 的真实正确响应，而 $θq,y∗(q)∗(N)\theta_{q,y^*(q)}^*(N)$ 代表针对具有计算预算 $N$ 的问题 $q$ 的测试时计算最优缩放策略。

1.指示函数 $I\mathbb{I}$ 的解释

指示函数 $Iy=y∗(q)\mathbb{I}_{y = y^{*}(q)}$ 的作用是判断 $y$ 是否等于 $y^{*}(q)$ 。具体来说：

如果 $y = y^{*}(q)$ ，则 $Iy=y∗(q)=1\mathbb{I}_{y = y^{*}(q)} = 1$ 。
如果 $\neq y^{*}(q)$ ，则 $Iy=y∗(q)=0\mathbb{I}_{y = y^{*}(q)} = 0$ 。

因此，指示函数实际上是在“指示”某个特定条件是否成立。在这个公式中，它用于判断模型的输出 $y$ 是否与正确答案 $y^{*}(q)$ 一致。

2.期望 $E\mathbb{E}$ 的解释

期望 $Ey∼Target(θ,N,q)\mathbb{E}_{y \sim \text{Target}(\theta, N, q)}$ 表示我们对 $y$ 从目标分布 $Target(θ,N,q)\text{Target}(\theta, N, q)$ 中采样时的平均值。具体来说，它计算的是 $Iy=y∗(q)\mathbb{I}_{y = y^{*}(q)}$ 的期望值，即 $y$ 等于 $y^{*}(q)$ 的概率。

因此，整个期望部分可以理解为：在给定参数 $θ\theta$ 、计算预算 $N$ 和问题 $q$ 的情况下，模型输出正确答案 $y^{*}(q)$ 的概率。

3.公式的整体解释

综合来看，公式的目标是找到一个最优的参数 $θ\theta$ ，使得在计算预算 $N$ 下，模型输出正确答案 $y^{*}(q)$ 的概率最大化。

3.2 3.2. 针对计算最优缩放估计问题难度

为了有效分析第2节所讨论的不同机制（例如提议分布和验证器）在测试时的缩放特性，我们将规定这个最优策略 $θq,y∗(q)∗(N)\theta^{*}_{q,y^{*}(q)}(N)$ 的一个近似值，使其作为给定prompt的一个统计量的函数。

统计量：比如prompt中a的个数，就是prompt的一个统计量。

该统计量会对给定prompt的难度概念进行估计。计算最优策略被定义为该prompt难度的函数。

策略=f(难度)

尽管这只是对公式1所示问题的一个近似解，但我们发现，相较于以临时或均匀抽样的方式分配推理时计算资源的基准策略，它仍能在性能上带来显著的提升。

这个theta不是真正的最优策略，而是我们根据prompt的一些特征，根据经验，猜测这样做会比较好。
因为是基于经验的猜测，所以是近似解。

我们对问题难度的估计会将给定问题划分到五个难度级别之一。然后，我们可以利用这种离散的难度分类，针对给定的测试时计算预算，在验证集上估计 $θq,y∗(q)∗(N)\theta^{*}_{q,y^{*}(q)}(N)$ 。接着，我们将这些计算最优策略应用于测试集。具体而言，我们会针对每个难度区间独立地选择性能最佳的测试时计算策略。通过这种方式，在设计计算最优策略时，问题难度可作为问题的一个充分统计量。

在统计学中，充分统计量是指对于一个未知的参数（在这个情境下，可能是和问题以及计算最优策略相关的参数），统计量包含了样本中关于该参数的所有信息。
简单地说，如果知道了这个充分统计量的值，就不需要其他关于样本的信息来推断这个参数了。
定义问题的难度。遵循莱特曼等人[22]的方法，我们将问题难度定义为给定基础大型语言模型（LLM）的一个函数。具体而言，我们把根据2048个样本估算出的模型在测试集中每个问题上的一次通过率（pass@1率）划分到五个分位数区间内，每个区间对应着难度递增的级别。我们发现，与MATH数据集中人工标注的难度区间相比，这种基于模型特定的难度区间概念能更好地预测使用测试时计算的效果。

问题难度的界定。参照莱特曼等人[22]的方法，我们将问题难度定义为给定基础大型语言模型（LLM）的一个函数。具体而言，我们把测试集中每个问题上模型的一次通过率（通过对2048个样本进行估算得出）划分到五个分位数区间内。

对于测试集中的每一个问题，模型会进行多次回答尝试（这多次尝试的结果构成了一个数据总体）。从这些结果中抽取 2048 个样本，用于估算模型在这个问题上的一次通过率（pass@1 率）。例如，如果模型对一个问题总共进行了 10000 次回答尝试，就从这 10000 次中选取 2048 次回答来计算它的 pass@1 率，即正确回答的次数占这 2048 次的比例。

每个区间对应着不断增加的难度等级。我们发现，与数学（MATH）数据集中人工标注的难度区间相比，这种基于模型特定难度区间的概念能更好地预测在测试阶段使用计算资源的效果。