剑指offer面试题53：在排序数组中数字出现的次数

索引请参考：系列目录

---

首先声明：本题是首次尝试完全在Ubuntu平台上发布。包括写博客、调试代码、牛客测试结果等。每天进步一点点!

---

题目

• 统计一个数字在排序数组中出现的次数
• 示例：
• 输入：
• {1,2,3,3,3,3,4,5} 和 3
• 输出 4

---

分析：

• 思路1：
  • （1）讲数组放入multiset中
  • （2）利用成员函数count寻找元素个数

思路2：二分法

• 看到排序数组最直接的方法就是想到二分法了吧～。具体算法原理和用处敬请期待。各位小伙伴也可以先上网搜一搜～
• 本题中通过二分法去查找数字的上下边界然后上下边界相减便得到了重复元素的个数。
  • （1）二分发寻找上下界
  • （2）球上下界的距离

---

思路1：

int GetNumberOfK(vector<int> data ,int k) {
        std::multiset<int>coll;
        for(auto elem : data)
            coll.insert(elem);
        return coll.count(k);
    }

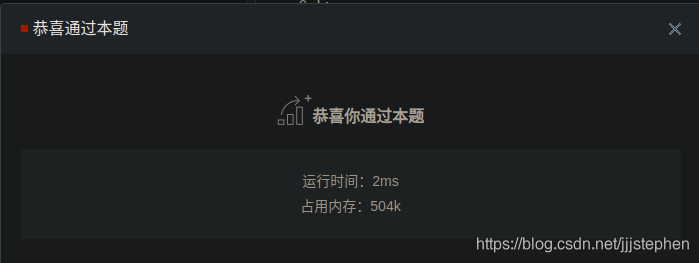
牛客运行结果：

思路2：二分法

int GetNumberOfK(vector<int> data ,int k) {
        int rbound = 0, lbound = 0;
		//1.寻找上界
		int l = 0, r = data.size();
		while (l < r)
		{
			int mid = l + (r - l) / 2;
			if (data[mid] <= k)
				l = mid + 1;
			else
				r = mid;
		}
		rbound = l;
		//2.寻找下界
		int ll = 0, rr = data.size();
		while (ll < rr)
		{
			int mid = ll + (rr - ll) / 2;
			if (data[mid] < k)
				ll = mid + 1;
			else
				rr = mid;
		}
		lbound = ll;
		return rbound - lbound;
    }

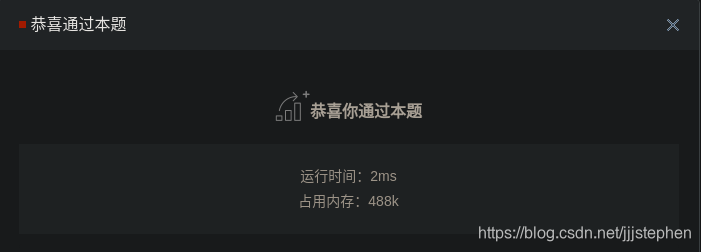
改进版二分法：

• 利用标准模板库进行测试结果同上。算法简单，一行解决。

int GetNumberOfK(vector<int> data ,int k) {
        return std::upper_bound(data.begin(), data.end(),k) - std::lower_bound(data.begin(), data.end(), k);
    }

评注：
（1）首先，通过上述三分demo，我们可以看出，从demo1到demo2，如果我们熟练掌握STL，这将会大大缩短我们的代码量。从demo2到demo3,如果我们掌握标准模板库的话，里面的好多算法可以供我们使用，若有兴趣还可以进行一番源码剖析。侯捷大大说过：对于标准模板库的作者们写出来的代码而言，我们写出来的代码都是很简陋的。源码剖析一来可以培养我们的逻辑思维，更能让我们的代码更加规范。
（2）上述代码时间复杂度分析：
* 思路1：

for(auto elem : data)
            coll.insert(elem);

o(n)

coll.count(k)

log(n)
综上，思路1的时间复杂度为：o(n)

• 思路2：可以看出整体的时间复杂度为o(n)
• 改进版同思路2