这篇博客详细介绍了数字信号处理的基础知识，包括线性卷积的运算，上采样和下采样的概念，相关函数的计算，以及圆周平移和反转。此外，还探讨了抽样前后连续频谱与离散频谱的关系，系统性质的判断，离散傅里叶变换(DFT)及其应用，如计算特定值和证明性质。博客还涵盖了Z变换的基本概念和应用，如初值定理、终值定理以及系统的幅频特性。
CHAPTER 2
2.基础知识：
1.线性卷积的表达式，运算
个人总结：
首先，线性卷积的表达式一定要记熟，才能开始下一步运算。
然后，如果已知h[n]、x[n]，求某个特定点y[n0]，一个比较快的方法是：观察定义式可以知道，式子里面的是x[k]h[n-k]，累加的项是k，
因此，以y[-1]为例，则
y[-1]=…+x[-3]h[2]+x[-2]h[1]+x[-1]h[0]+x[0]h[-1]+…
对于其他点原理也是一样的，即若求y[n0]，只要在x[n]和h[n]里分别找到下标x[nx]，h[nh]，满足nx+nh=n0，再将所有这些项相加即可。
该办法甚至可以用来求y[n]的通项式，非常简单。
2.上采样、下采样的定义
个人总结：
如果上采样率为L，则相当于：原本的x[n]每两个数之间内插（L-1）个0，变成x[n/L]
如果下采样率为M，则相当于：在原本的x[n]每M个就取一个数，变成x[Mn]
3.相关函数的运算
个人总结：
熟记表达式，并与线性卷积的表达式区分
相关运算用于信号检测、功率谱分析
卷积运算用于系统辨识、求线性时不变系统输出
4.圆周平移和圆周反转
个人总结：
圆周平移相当于整体循环移动，如果L＜N则混叠
圆周反转相当于除了n=0以外，整体下标n对应的数反转，即h[n]=h[N-n]。
更核心的方法是：知道模符号L的含义。(用于应付L＜N的奇奇怪怪的情况)
x[< f(n) >L]，0≤n≤N-1意味着将f(i)除以L，0≤i≤N-1，取余数m作为该位置i应该填的x[m]
对于多个< f(n) >L嵌套的情况，如x[<- < -n >2 >4]，从内到完成所有模的操作
例如：
x[n] = {x[0] x[1] x[2] x[3]}
1.L=N
y1[n] = x[< -n >4] :
{y1[0]， y1[1] ，y1[2]， y1[3]}
= {x[0] ，x[3] ，x[2] ，x[1]}
2.L<N
y2[n] = x[< -n >2] :
{y2[0]， y2[1]}
= {x[0]， x[1]}
3.混合型
y3[n] = x[<- < -n >2 >4] ：
{y3[0]， y3[1] ，y3[2] ，y3[3]} = :
mod(0,2)=0,mod(0,4)=0,∴y3[0] = x[0]
mod(-1,2)=1,mod(-1,4)=3,∴y3[1] = x[3]
mod(-2,2)=0,mod(0,4)=0,∴y3[2] = x[0]
mod(-3,2)=1,mod(-1,4)=3,∴y3[3] = x[3]
∴{x[0]，x[3]，x[0]，x[3]}
4.L>N
y4[n] = x[< -n >5] :
{y4[0]， y4[1] ，y4[2]， y4[3]，y4[4]}
= {x[0] ，x[4] ，x[3] ，x[2]，x[1]}
= {x[0] ，0，x[3] ，x[2]，x[1]}
2.可能的题型：
1.给定差分方程表征的系统，已知y[n0]，输入x[n]=f(n)，求系统的输出y[n]
2.给定差分方程表征的系统，求系统的冲激响应
3.给定系统框图，求系统的冲激响应
个人总结：
根据系统框图求冲激响应、根据冲激响应求系统框图是后面涉及到有理分式的频率响应以后避不开的内容。对于前者根据系统框图求冲激响应，最好的方法是:令系统中每个加法器的输出分别为一个函数，然后求出所有加法器各自的等式，最后化简
4.给定输出序列y[n]，系统序列h[n]，求输入序列x[n]
5.给定y[n]=f(sinω,cosω)（y[n]由sin和cos组成），求基波周期N
个人总结：
6.连续时间正弦序列x(t)抽样后得到的离散时间序列x[n]与原序列的关系：
个人总结：
7.给定y[n]=f(sinω,cosω)（y[n]由sin和cos组成），求功率
个人总结：
这是一道不知道窍门就很难做出来的题目。除去其他方法（例如：傅里叶级数），比较直接的方法是：写出周期序列的功率的定义式，然后将里面平方的部分尽可能展开，将所有频率分量相乘的部分尽量用三角函数公式展开，然后记住一点：对于周期为N的三角函数，
利用上式进一步化简，基本就能求出答案功率
CHAPTER 3
基础知识：
1.抽样前后连续频谱与离散频谱的关系
个人小结：
对连续序列抽样后，若连续频谱为Ga(jΩ)，离散频谱为G(ejω)，则抽样后得到的离散频谱相当于将连续频谱Ga(jΩ)，也就是Ga(jω)横轴先变成Ga(jω/T)，然后以2pi为周期平移，最后幅度变为原来的1/T
可能的题型
1.给定h[n],求DTFT H(ejω)
2.给定H(ejω)，求IDTFT h[n]
3.给定H(ejω)，求它的变化形式Y(ejω)=F(H(ejω))及其对应的y[n]（性质）
4.判断x[n]的奇偶性/X(ejω)是否有实部和虚部
个人总结：
关键是下面这个傅里叶变换对：
g[-n]→G(e-jω)（G(e-jω)相当于G(ejω)的共轭）
5.给定x[n]，不计算DTFT，求X(ejω)的特定值（定义，性质）
6.已知x(t)，系统抽样频率fS，求输出信号y[n]：
CHAPTER 4
4.基础知识：
1.系统性质的判断：线性，时不变性，因果性，稳定性
个人总结：
判断系统的性质从《信号与系统》就已经出现。这也是比较经典的题。而第四章判断系统性质的方法是基于y[n] = T[ x[n] ]，第六章涉及到传输函数H(z)以后，又会有另一套基于H(z)的判断方法，《信号与系统》中也会涉及到基于h[n]的判断方法。两类方法都需要牢记。
线性：y[n] = T[ x[n] ]，则y[n] = T[ ax1[n]+bx2[n] ] = ay1[n]+by2[n] = aT[ x1[n] ] + BT[ x2[n] ]
因果性：系统当前时刻n0的输出只由n≤n0时刻的输入决定
稳定性：若|x[n]|≤M，则|y[n]|≤常数
时不变性：时不变性的判断有点拗口，在判断时必须谨记：x[n-n0]是对n自身进行减n0的，y[n-n0]是在x[n]里面的最外层减0，同时也是对所有n进行减n0
例如y[n] = x[4n]
x[n-n0] = x[4(n-n0)]
y[n-n0] = x[4n-n0]
在此，顺便提及判断性质的各种方法
| 系统性质\函数类型\判断方法 | y[n] = f{x[n]} | 差分方程 | 冲激响应h[n] | 传输函数H(z) |
|---|---|---|---|---|
| 因果 | 输出只由当前或之前时刻的输入决定 | h[n] = h[n]·u[n] | 收敛域包括单位圆 | |
| 稳定 | 若x[n]＜M(有界)，则y[n]也有界 | h[n]绝对值的累加＜∞ | 极点都在单位圆内 |
2.系统输出的齐次解/全解/零输入响应/零状态响应
个人总结：
虽然有了z变换以后可以轻易写出全解，但有时候老师就是想刁难你考这些（当然也有可能不考）。以下是基本步骤
齐次解、特解、全解：
1.假定x[n]=0，y[n]＝λn，代入原差分方程得到λ的多项式，求出对应的λ的根λ1、λ2，对应的齐次解就是yc[n] = a1λ1n+a2λ2n
2.求特解yp[n]:
（a）当输入信号为常数x[n] = A·u[n]时，令yp[n] = B·u[n]
（b）当输入信号为指数x[n] = An时，令yp[n] = n·Bn
将上面假设的yp[n]代入到原差分方程，解出来的yp[n]就是特解。
3.全解y[n] = yc[n] + yp[n]
同时还要了解递归系统和非递归系统的区别。
递归系统：当前输出 = 当前输入 + 过去输入 + 过去输出
非递归系统：当前输出 = 当前输入 + 过去输入
4.可能的题型
1.判断系统是否满足xx性质
CHAPTER 5
5.基础知识：
1.离散傅里叶变换与反变换的定义式
个人总结：
每一种傅里叶变换的定义式都是必记项。尤其是观察累加的是哪一项（n），哪个是结果的自变量项（k）
2.DFT与DTFT的关系
个人总结：
DFT是DTFT的N点抽样
首先，对于在有限序列x[n]后面补零，补零前后得到的X[k]是不一样的。因为DFT加权的系数是WNnk=e-j2pi/N*kn，与序列的长度N有关，而DTFT加权的系数是e-jωn，与序列长度N无关。从另一个角度来讲，N代表了原本DTFT频域总共抽样的点数，点数不一样，抽样的间隔2pi/N不一样，抽样的位置也就不一样，得到的数也就不一样。
N与基波周期
其次，序列长度N也与基波周期有一定的联系。如果序列长度N是基波周期的整数倍，则得到的X[k]不会发生频谱泄露（频谱泄露的例子如下面有图所示），
再其次，若想用N点X[k]不混叠表示长度为M的x[n]对应的X(ejω)，必须满足N≥M
DFT的计算量
计算一次N点DFT，需要进行N2次复乘运算，N(N-1)次复加运算
当使用N点FFT后，需要进行(N/2)log2N次复乘运算，Nlog2N次复加运算
3.DFT序列的对称关系
个人总结：
最常用的关系，也是能够推导出其他关系的对称关系：
复序列x[n]：
实序列：
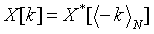
4.圆周卷积公式
个人总结：
看这个公式的时候，可以选择长度较小的序列，将圆周卷积结果试着展开来看看，并与线性卷积对比，方便理解
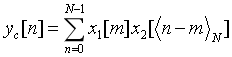
5.可能的题型
1.DFT性质的证明
个人总结：
这类题目很棘手很麻烦，因为就像一般的证明题一样，涉及到不少数学知识，需要练过手才知道大致思路。这里提供几个经常碰到的小技巧：
1）尽可能将已知的X[k]往这个方向靠：
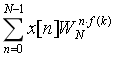
f(k)指化成k的函数。为了完成目标，常用的性质有下面这些：
2）W：
3）n（换元，换函数）：
经典的换元法：
更改累加符号的上下限：
换函数：
4）等比数列前N项求和公式
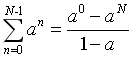
2.给定X[k]，不计算IDFT，求x[n]的特定值（定义，性质）
3.给定x[n]，不计算DFT，求X[k]的特定值（定义，性质）
4.DFT的对称关系（x[n]奇偶性、X[k]实虚、对称）
5.圆周卷积的应用（1个N计算2个N，2个N计算2N）
个人总结:
这类题目和证明题有一定的联系，因为先决的公式是经过推导的，这也就说明要是考场不会了可以临场证明，就是比较浪费时间（x）。想要更快做出来，最好的方法还是记熟基础知识，包括书本提到并亲自使用过的知识点、公式
6.实现圆周卷积
个人总结：
首先，最稳健的方法是利用圆周卷积的公式计算。其次还有其他好的方法，例如N×N矩阵法求N点的圆周卷积，这个需要根据圆周卷积的定义式记住矩阵每一行的元素。还有一个通用的方法是利用线性卷积实现圆周卷积，该方法同样是利用圆周卷积求线性卷积的重要依据，具体思路如下：
对于两个长度为M和N的序列x1[n]和x2[n]，要实现L点圆周卷积
当L<M+N-1时，其L点圆周卷积 = 线性卷积结果的L点周期延拓混叠相加，只有在M+N-1-L≤n≤L-1范围内的结果才是线性卷积的结果。
当L>M+N-1时，其L点圆周卷积相当于线性卷积后补零直到长度=L。
CHAPTER 6
基础知识：
1.初值定理，终值定理，z变换的性质
个人总结：
首先是初值定理和终值定理的定义和适用范围：
初值定理：
终值定理：若H(z)所有极点都在单位圆|z|=1内，则有
然后是z变换的具体性质。其中最膈应人的变换应该是
2.z变换的定义
个人总结：
z变换最容易想到的是有理z分式的变换，因为这里面一是涉及到z变换常用序列，
二是涉及到部分分式法。这里面解决有两个方法，一是最简单粗暴的慢慢算未知数，另一种方法可以较快计算未知数，如下所示：
这里还有第三种方法求逆z变换，也就是长除法，但是该方法用于求有限长h[n]，因为求出来的是z-n的多项式，对应的就是h[n]每一项的系数
提到有理z分式，另一个比较常考的就是H(z)对应的差分方程表达式，这个也比较简单。
变换前后，极其需要注意的一个知识点是收敛域，这一点需要以下这些知识点结合来判断：序列的性质（是否因果？左边or右边？…），z变换的性质
序列的收敛域：
1）因果序列h[n]，其H(z)的收敛域包括单位圆
2）有限长序列，收敛域覆盖在整个z平面，但可能要去除z=0或z=∞这两个点
注：
对于有限长序列，可以自己建立一个FIR滤波器形式的h[n]来验证它的收敛域是否包含z=0或z=∞
3）右边序列，收敛域在z平面上通过离原点z=0最远的极点的圆的外部
4）左边序列，收敛域在z平面上通过离原点z=0最近的极点的圆的内部
5）无限长双边序列，收敛域是以通过极点的两个同心圆为界的环，且环内没有极点
z变换里面会改变收敛域的操作：
假设原本的收敛域为R
1）时间反转：1/R
2）线性，卷积：包括R1∩R2
3）时移，差分：R，可能除了点z=0或z=∞
3.系统的幅频特性
个人总结：
对于H(z)，系统的幅频特性/幅度函数等于零点矢量的长度除以极点矢量的长度（这里矢量的长度指的是从零点/极点到|z|=1的圆的长度）。为了求出长度，经常需要余弦定理，即：若某个夹角为ω，其邻边为a、b，对边为c，则c2 = a2+b2-2ab·cosω
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
