莫队算法学习

参考博客：

1.https://blog.youkuaiyun.com/hnshhslsh/article/details/50582926

2.https://blog.youkuaiyun.com/thinfatty/article/details/72581276

莫队算法其实是一种离线的暴力算法。

 

我们看下HYSBZ - 2038。

题意：小明有m只袜子，现在他要从【L,R】的袜子中选出相同颜色的袜子，问这样的概率是多少。

 

首先我们考虑一下暴力：

对每个区间我们都遍历一次，统计相同颜色的袜子数目，然后答案就是sum(C(i,2))/C(R-L+1,2)。显然这样的时间复杂度是0(n*m)。

我们这样暴力：

add(position):

  count[array[position]]++

  if count[array[position]]== 3:

    answer++

 

remove(position):

  count[array[position]]--

  if count[array[position]]== 2:

    answer--

 

currentL = 0

currentR = 0

answer = 0

count[] = 0

for each query:

  // currentL 应当到 L, currentR 应当到 R

  while currentL< L:

    remove(currentL)

    currentL++

  while currentL> L:

    add(currentL)

    currentL--

  while currentR< R:

    add(currentR)

    currentR++

  while currentR> R:

    remove(currentR)

    currentR--

  output answer

我们看下莫队算法是怎样处理的：

首先考虑下面的数据

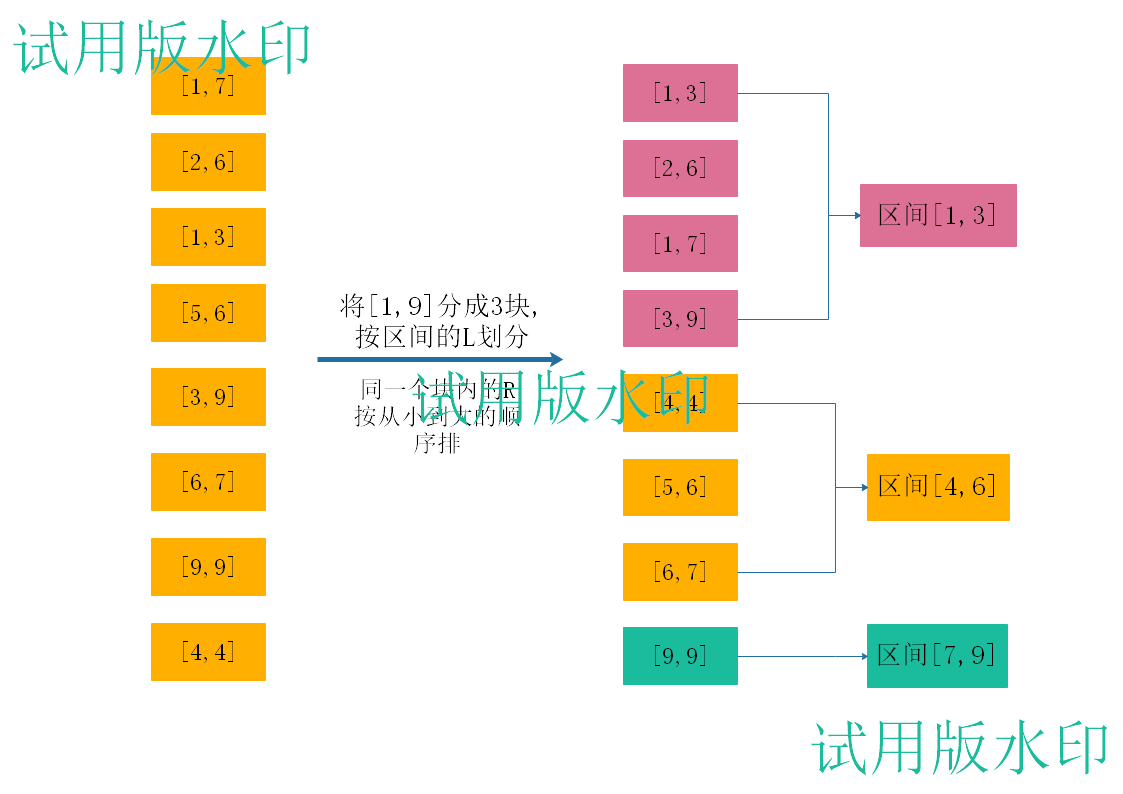
先对区间的L进行分块，一共分成3块，【1,3】，【4,6】，【7,9】。

然后对每一块内的R按从小到大排序。

我们任然像上面那样暴力。右指针在每个块内最多移动n下，一共个sqrt(n)块，复杂度是nsqrt(n)。左指针在每个块内最多移动sqrt(n)下，一共m个查询，最多移动msqrt(n)次。所以最终的复杂度是nsqrt(n)。我们仅仅简单的排了个序，时间复杂度就降低了很多。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <set>
#include <map>

using namespace std;

typedef long long llt;

const int N = 50010;
const int M = 50010;
const int INF = 0x3fffffff;
const int mod = 1e9+7;

struct Node{
    int l,r,id,block;
    bool operator < (const Node&a) const{
        if(a.block == block) return r < a.r;
        else return block < a.block;
    }
}node[N];

llt cnt[N],mole[N],deno[N],data[N];
llt ans;

void init()
{
    ans = 0;
    memset(cnt,0,sizeof(cnt));
}

llt cal(llt a)
{
    if(a < 2) return 0;
    else return a*(a-1)/2;
}

llt gcd(llt a,llt b)
{
    if(b == 0) return a;
    else return gcd(b,a%b);
}

//莫队算法

//添加一个点
void Add(int pos)
{
    llt a = ++cnt[data[pos]];
    ans += cal(a)-cal(a-1);
}

//去除一个点
void Remove(int pos)
{
    llt a = --cnt[data[pos]];
    ans -= cal(a+1)-cal(a);
}

void solve(int n)
{
    int L,R,cl = 1,cr = 1; Add(1);
    for(int i = 1; i <= n; ++i){
        L = node[i].l; R = node[i].r;
        while(cl < L){ Remove(cl); cl++; }
        while(cl > L){ cl--; Add(cl); }
        while(cr < R){ cr++; Add(cr); }
        while(cr > R){ Remove(cr); cr--; }
        mole[node[i].id] = ans;
        deno[node[i].id] = cal(R-L+1);
    }
}

int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m)){
        init();
        for(int i = 1; i <= n; ++i) scanf("%lld",&data[i]);
        int a,b,block = 0;
        for(int i = 1; i <= m; ++i){
            scanf("%d%d",&a,&b);
            node[i].l = a; node[i].r = b; node[i].id = i;
            block = max(block,b);
        }
        for(int i = 1; i <= m; ++i){
            node[i].block = (int)node[i].l/sqrt(block);
        }
        sort(node+1,node+m+1);
        solve(m);
        for(int i = 1; i <= m; ++i){
            llt t = gcd(deno[i],mole[i]);
            deno[i] /= t; mole[i] /= t;
            printf("%lld/%lld\n",mole[i],deno[i]);
        }
    }
    return 0;
}