可持续化线段树学习

参考博客：https://www.cnblogs.com/shenben/p/5598371.html

什么是可持久化数据结构：

可持久化数据结构(Persistent data structure)就是利用函数式编程的思想使其支持询问历史版本、同时充分利用它们之间的共同数据来减少时间和空间消耗。

通过hdu2665来理解可持久化线段树

题意：求区间第k大的数

首先在这里我们可以建立n颗线段树，第i颗线段树表示对区间[1,i]的所有data[i]建立线段树，而线段树的区间范围是区间[1,n]的取值范围。因为data[i]的数据可能很大，我们先对它进行离散化处理。

下面举个例子：有个数列{4,3,10,7}，离散化之后3-->1,4-->2,10-->4,7-->3。

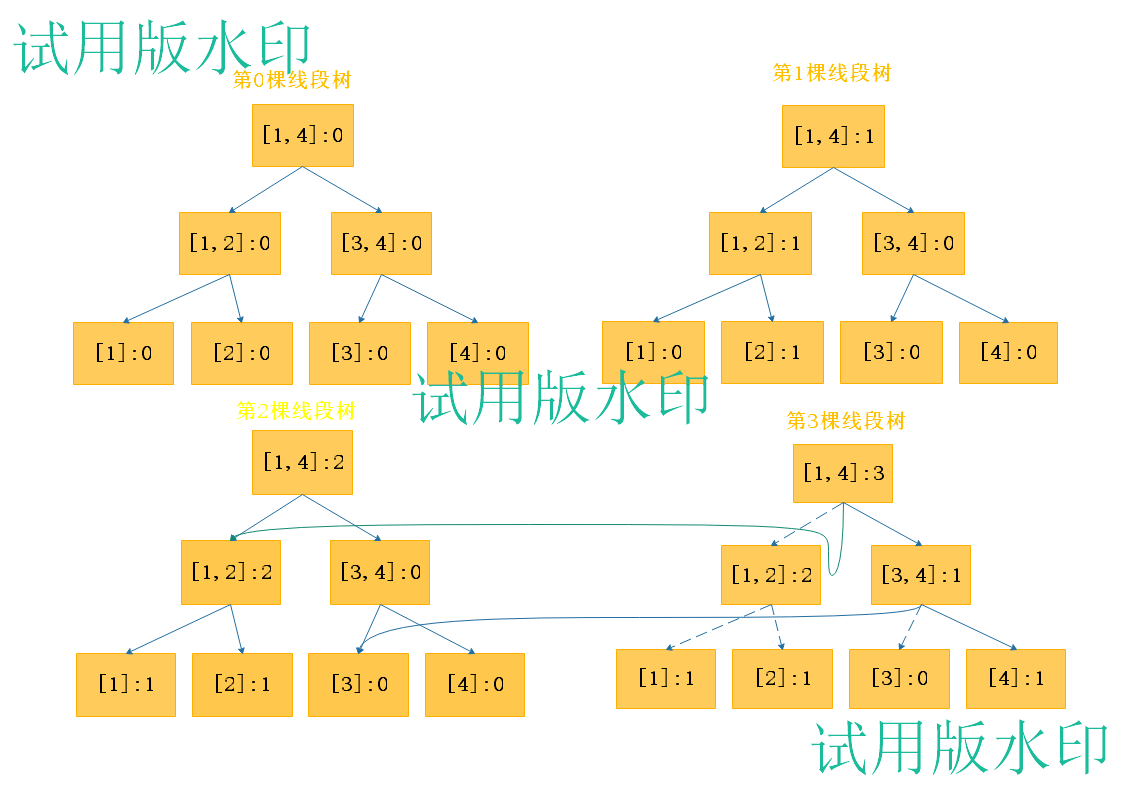
我们怎么求区间[x,y]的第k大？

这时我们考虑第x-1棵线段树，和第y棵线段树。两颗线段树在根节点[1,m]的差值就是区间[x,y]的元素个数。res = Tr[y].lc.cnt-Tr[x-1].rc.cnt > k,则说明第k大在区间[1,mid]内，否则在[mid+1,m]区间内，这时我们在这个区间内找第k-res大的数。

这样建n颗线段树，肯定会MLE的，我们观察下第i，i+1棵线段树。在第i颗线段树的基础上插入data[i+1]就得到了第i+1棵线段树，所以第i+1棵线段树与第i棵线段树只有logm个结点不同，因此我们只要添加logm个结点，其他节点与第i棵线段树公用即可。这样的空间复杂度是n*4+nlogm（m是线段树区间范围），时间复杂度是2nlogm。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>
#include <set>
#include <map>

using namespace std;

typedef long long llt;

const int N = 100010;
const int M = 50010;
const int INF = 0x3fffffff;

//静态求第k小的数
//可持久化线段树

struct Node{
    int lc,rc;
    int cnt;
}node[N*20];

int cur,data[N],ha[N],root[N];
int n,m;
map<int,int>mp;   //map太烧内存了，2个map会爆内存

void init()
{
    cur = 0;
    mp.clear();
}

//离散化
int Hash()
{
    for(int i = 0; i < n; ++i) ha[i] = data[i];
    sort(data,data+n);
    int sz = unique(data,data+n)-data;
    for(int i = 0; i < n; ++i){
        int t = ha[i];
        ha[i] = lower_bound(data,data+sz,t)-data+1;
        mp[ha[i]] = t;
    }
    return sz;
}

inline void PushUp(int rt)
{
    node[rt].cnt = node[node[rt].lc].cnt+node[node[rt].rc].cnt;
}

int Build(int l,int r)
{
    int k = cur++;
    if(l == r){
        node[k].cnt = 0;
        return k;
    }
    int mid = (l+r)>>1;
    node[k].lc = Build(l,mid);
    node[k].rc = Build(mid+1,r);
    PushUp(k);
    return k;
}

//rt表示前一颗线段树的根节点,pos表示第i个点的值，val表示数量
int Update(int rt,int l,int r,int pos,int val)
{
    int k = cur++;
    node[k] = node[rt];
    if(l == pos && r == pos){
        node[k].cnt += val;
        return k;
    }
    int mid = (l+r)>>1;
    if(pos <= mid) node[k].lc = Update(node[rt].lc,l,mid,pos,val);
    else node[k].rc = Update(node[rt].rc,mid+1,r,pos,val);
    PushUp(k);
    return k;
}

int Query(int l,int r,int rt1,int rt2,int kth)
{
    if(l == r) return l;
    int mid = (l+r)>>1;
    int res = node[node[rt1].lc].cnt-node[node[rt2].lc].cnt;

    if(kth <= res) return Query(l,mid,node[rt1].lc,node[rt2].lc,kth);
    else return Query(mid+1,r,node[rt1].rc,node[rt2].rc,kth-res);
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        init();
        scanf("%d%d",&n,&m);
        for(int i = 0; i < n; ++i){
            scanf("%d",&data[i]);
        }
        int mx = Hash(),rt;

        rt = Build(1,mx);
        root[0] = 0;
        for(int i = 0; i < n; ++i){
            rt = Update(rt,1,mx,ha[i],1);
            root[i+1] = rt;
        }
        int a,b,c;
        for(int i = 0; i < m; ++i){
            scanf("%d%d%d",&a,&b,&c);
            int ans = Query(1,mx,root[b],root[a-1],c);
            printf("%d\n",mp[ans]);
        }
    }
    return 0;
}