广搜（BFS）

#############

#S . .## . . .####

# .# . . . .# . .###

# .# .##### . .##

# .# . . . .### .E#

#############

深搜经典

由上下左右的顺序进行深度游搜索（不撞南墙不回头）

因此深搜算法找到的首个解往往不是最优解。

换句话说,使用深搜找最短的路线,就必须把所有可能的路线都尝试一遍,才能确定哪个路线是离起点步数最少的。

然而深搜的时间复杂度很高,迷宫尺寸每+1,则所有路径搜索一遍所耗的时间是呈指数型增长的。

例如6x6的迷宫,深搜1秒内可以搜索完全部路径。而10x10的迷宫,耗时一年甚至上百年也搜索不完所有的路径

如果有这么一种搜索方式,能够像水滴落在平静的水面一样一圈一圈扩散出去,则第一次找到出口时,一定是最短的路线。

广度优先搜索：

广度优先搜索算法就是以这种一圈一圈(一

层一层)扩散的搜索方式来进行的。

那为什么以这样的方式搜索,找到出口时走

过的路线一定是最短的呢?

例如以下无障碍物的迷宫,起点附近有几个宝

箱,问从起点到每个宝箱最少分别需要多少步?

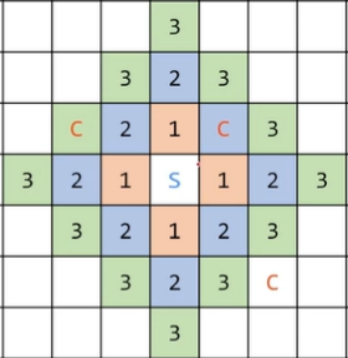
那广度优先搜索如何用代码实现呢?

在这之前先思考一个问题:

根据广搜的特点,必须先将步数为1的格子全

部搜索过之后,才能开始搜索步数为2的格子。

那对于步数1的情况,很显而易见是起点上下

左右四个方向的格子。但是步数2的格子如何确

定及如何表示呢?

但是广搜的特性,还没搜索完步数1的格子就不能进行步数2格子的搜索。那我能不能先将这些格子的坐标储存起来,等步数1的格子搜索完了再根据储存的坐标进行步数2的搜索呢?

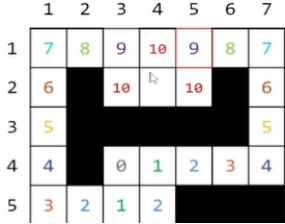
注意:此时找到出口了,但是队列里仍然

有未使用完的数据。

事实上,只要队列里还有数据,广搜就仍可继续。但如果直到队列为空仍然未搜索到答案,则说明无解。

void bfs (){
	quewe<数据类型>q;
	q.push(初始状态);//对于迷宫问题,初始状态就是起点坐标
	while(!q.empty()){//队列中还有元素就出队并搜索
		//队头出队
		数据类型 队头元素=q.front();
		q.pop();
		if(找到答案)计算答案(并退出);//也可不return,继续搜索
		//搜索队头元素下一步所有可去的相邻状态(位置)
		for(int i=1;i <= 相邻状态(位置)种类;++i){
			if(满足扩展条件(如未被标记)){
				做些什么(例如迷宫中计算到达该位置的步数);
				该状态(位置)打上标记;
				q.push(i对应的状态(位置));
			}
		}
	}
}